Уравнение неразрывности

Воспользовавшись свойством недеформируемости и непроницаемости стенок элементарной сруйки, на основании ЗСМ можно написать:

dM₁ = dM₂ = … = dM_n = const

Массовый расход можно выразить через объемный:

dM₁ = r₁dQ₁ = r₁w₁dS₁

dM_n = r_ndQ_n = r_nw_ndS_n

r₁w₁dS₁ = r₂w₂dS₂ = … = const

Для несжимаемой жидкости плотность одинакова: r₁ = r₂ = …, тогда:

w₁dS₁ = w₂dS₂ = … = const

— уравнение неразрывности для сечения струйки.

Учитывая, что поток есть совокупность элементарных струек, запишем уравнение неразрывности для потока:

w₁S₁ = w₂S₂ = … = const

Средняя скорость движения в потоке обратно пропорциональна площади живых сечений, то есть с уменьшением сечения скорость возрастает.

Дифференциальные уравнения движения идеальной
(невязкой) жидкости (уравнения Эйлера)

Рассмотрим неустановившееся движение идеальной жидкости в декартовой системе координат. Для этого выделим элементарный объем dxdydz. На этот объем действуют массовые и поверхностные силы.

Сумма действующих сил равна силе инерции массы жидкости, находящейся в этом объеме.

F_z + P_z = R_z

F_x + P_x = R_x

F_y + P_y = R_y

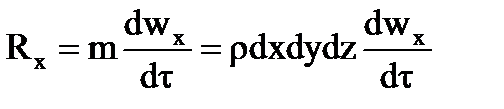
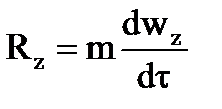
После соответствующих математических преобразований получим:

Для установившегося движения:

Диффренциальные уравнения движения реальной жидкости
(уравнение Навье—Стокса)

При движении реальной жидкости наряду с силами давления возникают силы внутреннего трения. Тогда можно записать:

Если выразить силу трения между слоями движущейся жидкости по уравнению Ньютона—Петрова и воспользоваться результатом вывода дифференциальных уравнений движения идеальной жидкости, то после соответствующих преобразований можно получить следующее:

Общего решения не имеют ни дифференциальные уравнения движения идеальной жидкости, ни тем более реальной. Известны только частные случаи.

Лекция 7Уравнения Бернулли для идеальной и реальной жидкости. Основные уравнения движения потока.

Уравнения Бернулли