Правила вычисления производной.
1. 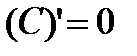 .
.
Док-во:
Дадим x приращение Dx, 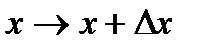 . Тогда функция получит приращение Dy. Отсюда
. Тогда функция получит приращение Dy. Отсюда 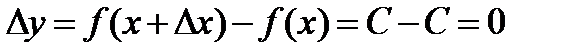 . Так как
. Так как 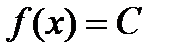 , то
, то 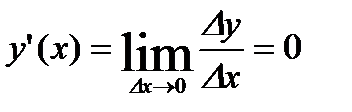 . Þ (C)¢=0.
. Þ (C)¢=0.
Ч.т.д.
2. Если функции u и v имеют конечные производные, то производная суммы (разности) равна сумме (разности) производных: 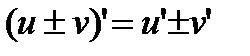 .
.
Док-во:
Дадим x приращение Dx, 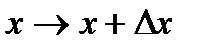 . Тогда функция
. Тогда функция 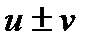 получит приращение
получит приращение 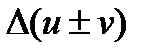 . Отсюда
. Отсюда 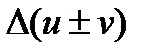 =
= 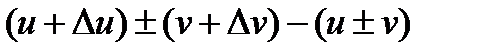 =
= 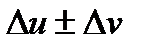 .
.
Þ 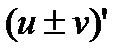 =
= 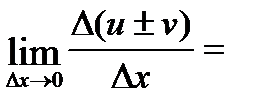
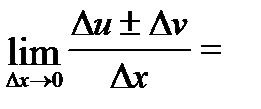
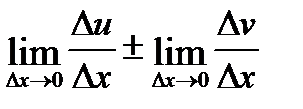 =
= 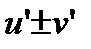 .
.
Ч.т.д.
3. Если функции u и v имеют конечные производные, то производная произведения находится по формуле: 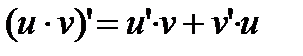 .
.
Доказывается аналогично второму.
Следствие: Константу можно выносить за знак произведения: 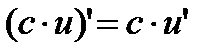 .
.
4. Если функции u и v имеют конечные производные, то производная частного находится по формуле: 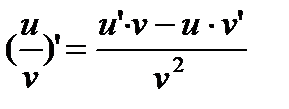 , где v¹0.
, где v¹0.
Таблица простейших производных.
| Степенные функции | |||
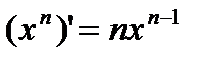
| 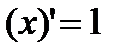
| 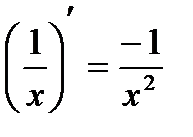
| 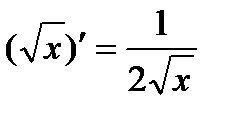
|
| Показательные функции | Логарифмические функции | ||
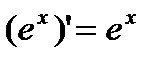
| 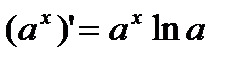
| 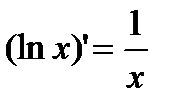
| 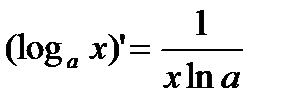
|
| Тригонометрические функции | |||
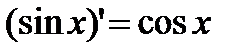
| 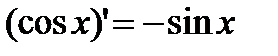
| 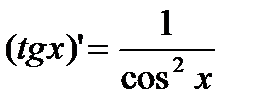
| 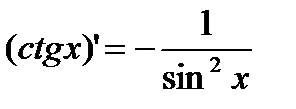
|
| Обратные тригонометрические функции | |||
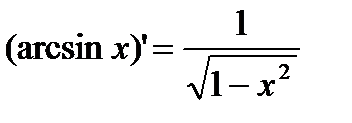
| 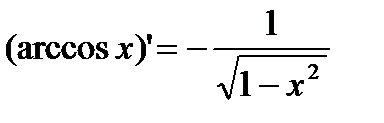
| 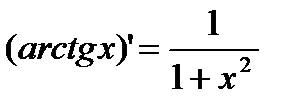
| 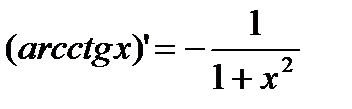
|
Производные тригонометрических функций.
1) 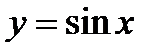 .
.
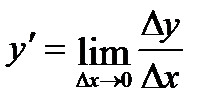 =
= 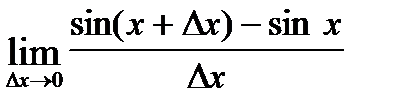 =
= 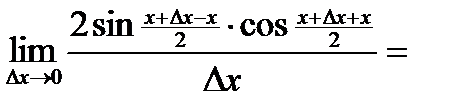
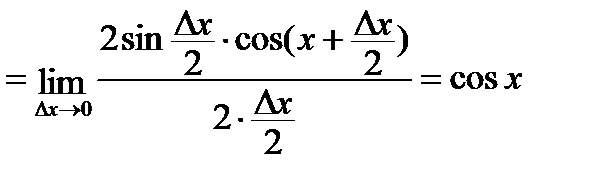 . Þ
. Þ 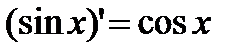 .
.
2) 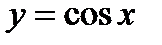 .
.
Доказывается аналогично первому: 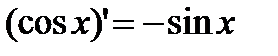 .
.
3) 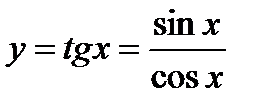 .
.
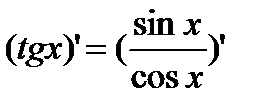 =
= 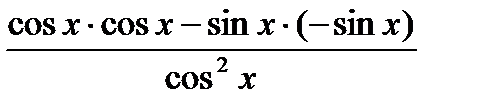 =
= 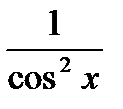 Þ
Þ 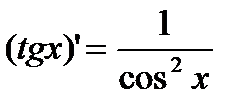 .
.
4) y=ctg x. 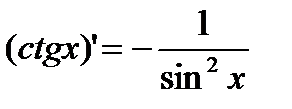 .
.
Производные обратных тригонометрических функций.
1) y=arcsin x. 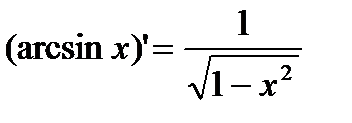 .
.
2) y=arccos x. 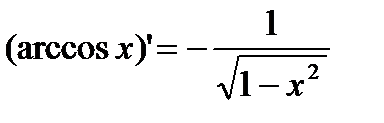 .
.
3) y=arctg x. 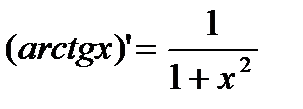 .
.
4) y=arcctg x. 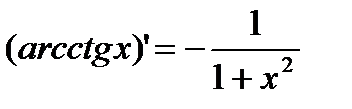 .
.
Дата добавления: 2015-11-06; просмотров: 685;
