Дифференциал функции.
Пусть функция 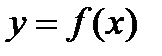 определена в точке x0 и ее окрестности. Дадим x0 приращение Dx, тогда функция получает приращение Dy:
определена в точке x0 и ее окрестности. Дадим x0 приращение Dx, тогда функция получает приращение Dy: 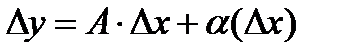 , где А - число, a(Dx) - б/м более высокого порядка малости чем Dx. Выражение A×Dx называют главной частью приращения Dy.
, где А - число, a(Dx) - б/м более высокого порядка малости чем Dx. Выражение A×Dx называют главной частью приращения Dy.
Определение: Дифференциалом функции 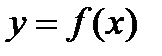 называют главную часть ее приращения, линейную относительность Dx.
называют главную часть ее приращения, линейную относительность Dx.
Обозначают: dy или df, dy=df=A·Dx, где Dx ® 0.
Определение: Функция, имеющая дифференциал в точке x0, называется дифференцируемой в этой точке.
Теорема: Для того чтобы функция 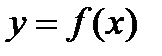 была дифференцируема в точке x0 необходимо и достаточно, чтобы она имела в точке x0 конечную производную.
была дифференцируема в точке x0 необходимо и достаточно, чтобы она имела в точке x0 конечную производную.
Дифференциал 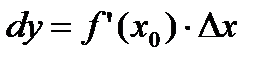 , где Dx – приращение аргумента и обозначается dx, тогда окончательно дифференциал:
, где Dx – приращение аргумента и обозначается dx, тогда окончательно дифференциал:
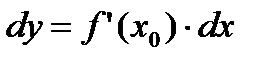 .
.
Пример: 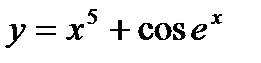 Þ
Þ 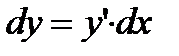 Þ
Þ 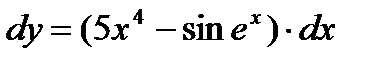 .
.
Геометрический смысл дифференциала.
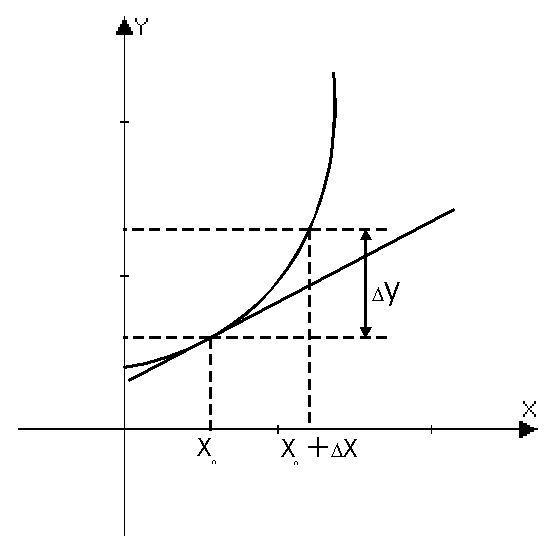 Из треугольника:
Из треугольника: 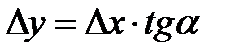 . Þ
. Þ 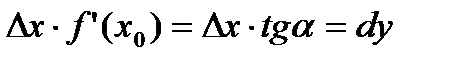 ,
,
где 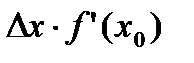 — геометрический смысл производной.
— геометрический смысл производной.
Дифференциал – это приращение ординаты касательной, проведенной к кривой в точке касания x0.
Правила нахождения дифференциала.
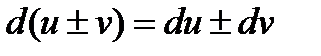
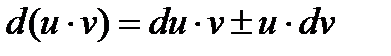
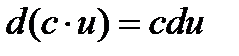
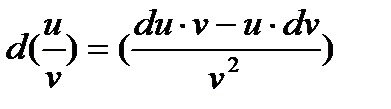
Дата добавления: 2015-11-06; просмотров: 830;
