Теоремы о линейно зависимых системах векторов линейного пространства.
Теорема 1. Необходимое и достаточное условие линейной зависимости.
Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой-нибудь вектор этой системы был линейной комбинацией всех остальных.
Док-во: Необходимость ( ).
Дана ЛЗ система. Нужно доказать, что один вектор ЛК всех остальных.
а1, а2, а3, … аn – ЛЗ система векторов, т.е. среди α1, α2 ,α3 … αn существует число отличное от нуля так, что ЛК α1 а1+ α2 а2+α3 а3+…+ αn аn= 0.
Положим для определения, что коэффициент α1 ≠ 0. Разделим обе части последнего равенства на α1 ≠ 0:
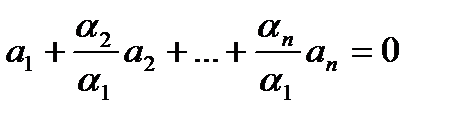 ;
;
 .
.
Отсюда следует, что а1 - ЛК остальных векторов.
Необходимость доказана.
Достаточность ( ).
Пусть один вектор – это линейная комбинация остальных. Нужно доказать, что система векторов ЛЗ.
Пусть αn = α1 а1+ α2 а2+α3 а3+…+ αn-1 аn-1.
α1 а1+ α2 а2+α3 а3+…+ αn-1 аn-1- 1αn = 0.
Так как есть не нулевой коэффициент, то система векторов а1, а2, а3, … аn- линейно зависима.
Ч.т.д.
Теорема 2. Система, содержащая нуль-вектор, линейна зависима.
Док-во: Рассмотрим систему векторов, содержащую нуль-вектор. а1, а2, а3, … аn,Ө, где Ө ‒ нуль-вектор. Очевидно, что имеет место следующее равенство 0·а1+ 0· а2+0· а3+…+ 5·Ө = 0.
Есть не равный нулю коэффициент, равный 5, а линейная комбинация равна 0, отсюда следует, что система векторов ЛЗ.
Ч.т.д.
Теорема 3. Система, содержащая линейно зависимую подсистему, тоже будет линейно зависима.
Док-во: Рассмотрим систему векторов а1, а2, …,ак, ак+1 … аn, где а1, а2,…, ак - линейно зависимый кусочек. α1 а1+ α2 а2+ … +αкак= 0. Есть коэффициент отличный от нуля.
Очевидно, что с этими же коэффициентами будет выполняться равенство
α1 а1+ α2 а2+…+αк ак+…+0· ак+1+…+ 0·αn = 0.
Отсюда следует, что система векторов ЛЗ.
Ч.т.д.
Дата добавления: 2015-11-06; просмотров: 852;
