Запись силлогизмов на языке логики предикатов

В § 4 главы 6 мы рассматривали язык логики предикатов (ЯЛП), который позволяет выявить логическую форму простых, в частности, категорических, суждений. Носкольку категорический силлогизм состоит из категорических суждений, мы можем записать их на символическом языке подобно тому, как делали это с умозаключениями логики суждений при помощи языка логики суждений (ЯЛС).

При помощи ЯЛСа мы не могли записать наши силлогизмы, потому что последние основываются на анализе внутренней структуры высказываний, тогда как ЯЛС не принимает ее во внимание. ЯЛП позволяет записать силлогистические умозаключения. Запись на ЯЛПе категорических суждений мы приводили в § 4 главы 6.

Пример. Силлогизм по первой фигуре, модус ААА:

Все M есть P.

Все S есть M.

Все S есть P.

предстанет в следующем виде:

├

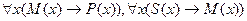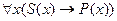
Пример. Силлогизм по второй фигуре EIO:

Ни один P не есть M.

Некоторые S есть M.

Некоторые S не есть P.

предстанет в следующем виде:

├ .

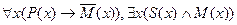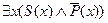Подобным же образом мы можем записать остальные силлогизмы: как непосредственные, так и опосредованные.

§ 4. Способы проверки правильности силлогизмов

Задача логики - отделять правильные рассуждения от неправильнщх. Естественно, эту же задачу приходится решать и по отношению к силлогизмам. Практически все рассуждения, приведенные ранее (за исключением примера рассуждения в диалоге из § 1 этой главы), являются правильными. Но мы знаем из практики нашего ежедневного общения, что вообще-то неправильные рассуждения встречаются довольно часто. Возникает задача: каким образом критиковать неправильные рассуждения? Эту задачу решают способы проверки правильности силлогизмов.

Всего таких способов три:

1) построение круговых схем для посылок и заключения силлогизмов;

2) предъявление контрпримера;

3) проверка на соответствие общим правилам силлогизмов и правилам фигур.

Рассмотрим эти способы по отдельности.

1) Построение круговых схем для посылок и совмещение их на одной схеме.

Это - самый простой способ проверки. В правильном силлогизме совмещение круговых схем, построенных для каждой из посылок, должно дать однозначный результат, совпадающий с отношением между меньшим и большим термином в заключении.

Пример.

Все юристы знают признаки преступления.

Никто из присутствующих не знает признаков преступления.

Никто из присутствующих не является юристом.

Это - вторая фигура, модус АЕЕ.

Обозначим термины: “юрист” - через P, “человек, который знает признаки преступления” - через M, “присутствующий” -через S. Тогда для большей посылки мы получим следующую схему:

Для второй посылки, соответственно, следующую схему:

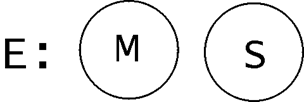
Совмещение этих схем даст следующий результат:

Мы видим, что других отношений между S и P быть не может, т.е. мы получили однозначный результат. Наше заключение «Ни один S не есть P» на этой схеме истинно. Это означает, что при истинности посылок заключение обязательно истинно, а значит исходное умозаключение правильно.

Пример.

Все юристы знают признаки преступления.

Все присутствующие знают признаки преступления.

Все присутствующие являются юристами.

Это также вторая фигура, модус ААА. Обозначим термины силлогизма так же, как в предыдущем примере. Тогда для большей посылки получится схема, как в предшествсющем примере.

Для меньшей посылки получится следующая схема:

Совмещаем эти схемы на одной круговой схеме:

Мы видим, что эти схемы можно совместить по-разному, т.е. мы не получили однозначного результата. Причем на совмещенной схеме (а) наше заключение истинно, а на совмещенной схеме (б) наше заключение ложно. Как интерпретировать результаты нашего совмещения круговых схем для посылок? Вспомним, что в правильном дедуктивном умозаключении посылки и заключение должны находиться в отношении логического следования. Вместе с тем мы знаем, что отношение логического следования отсутствует там, где посылки могут быть истинными, а заключение ложным. (Вспомните наши отношения между сложными суждениями!) Эти отношения мы можем перенести и на совмещенные круговые схемы и сказать, что если существует такая совмещенная схема, на которой посылки истинны, а заключение ложно, то наш силлогизм не является правильным. В нашем случае такая схема существует - это схема (б). Следовательно, наш силлогизм неправилен.

Отсюда ммжно получить общий критерий правильности силлогизмов:

Силлогизм является правильным, если нельзя построить такую совмещенную круговую схему, на которой обе посылки являются истинными, а заключение - ложным.

Отсюда следует и критерий неправильности силлогизмов:

Силлогизм является неправильным, если можно построить хотя бы одну такую круговую схему, на которой обе посылки являются истинными, а заключение - ложным.

Пример. Применим разработанный метод для обсуждения рассуждения о спартанцах и их вкладе в философию, который поставил в тупик персонажей нашего диалога в § 1 этой главы. Воспроизведем последний из обсуждавшихся там силлогизмов еще раз.

Некоторые древние греки внесли вклад в развитие философии.

Все спартанцы - древние греки.

Некоторые спартанцы внесли вклад в развитие философии.

Это - первая фигура, модус IAI. Обозначим больший термин - “те, кто внес вклад в развитие философии” - через P, средний - “древние греки” - через M, а меньший - “спартанцы” - через S. Тогда круговая схема, соответствующая большей посылке, будет выглядеть следующим образом:

а круговая схема, соответствующая меньшей посылке:

Cовместив их, получаем:

На этой диаграмме заключение “Некоторые спартанцы внесли вклад в развитие философии” – ложно а обе посылки истинны. Следовательно, может быть построена такая совмещенная схема, на которой посылки истинны, а заключение - ложно, а значит, рассматриваемое умозаключение неправильно.

Пояснение. Построение круговых схем - это не аргумент в споре. Вряд ли вам кого-либо удастся убедить в своей правоте, если вы будете рисовать схемы. Однако они помогут уяснить вам ситуацию, понять, что же неправильно в аргументации Вашего оппонента, и задать ему, например, такой вопрос: “Вы уверены, что спартанцы относятся именно к тем грекам, которые внесли вклад в философию? А не может ли быть так, что они относятся как раз к той части греков, которые никакого вклада в философию не вносили?” И пусть теперь он попытается более или менее убедительно ответить на ваши вопросы. Инициатива перешла к вам. А сформулировать такие вопросы, которые представляют затруднение для оппонента, помогли нам именно круговые схемы, наглядно показывающие, что именно нужно спросить.

2) Предъявление контрпримера.

Способ обнаружения неправильности умозаключений путем построения круговых схем все же не приводит к убедительной победе в дискуссии. Он, скорее, носит теоретический характер. Как же опровергать умозаключения на практике так, чтобы неправильность умозаключения Вашего оппонента была бы всем совершенно очевидной и тем самым обеспечивала бы вам победу в споре? Для этой цели подходит предъявление контрпримера.

Контрпример - силлогизм, тождественный с данным по форме (т.е. имеющий ту же фигуру и тот же модус), но абсурдный по смыслу.

Что значит «абсурдный по смыслу»? Это означает, что посылки контрпримера должны быть очевидно истинными суждениями, а заключение очевидно ложным. Это и производит впечатление абсурдности умозаключения. Основанием метода контрпримера является живущее в нашей душе требование к правильным умозаключениям: в них из истинности посылок обязательно должна следовать истинность заключения, а если заключение (при истинных посылках) явно ложно, то это наше чувство возмущается и свидетельствует против данного умозаключения.

По отношению к умозаключению о спартанцах и философии задача поиска и предъявления контрпримера решается следующим образом. Мы ищем умозаключение по первой фигуре, модус IАI. Этот модус, как мы теперь знаем, не относится к числу правильных. Однако нам это еще надо продемонстрировать аудитории. Как показывает построенная ранее круговая схема, нам нужно найти такие понятия M и P, которые находились бы в отношении перекрещивания, и такое понятие S, объем которого очевидно исключался бы из объема понятия P. Здесь требуется некоторое творчество. Но, по крайней мере, круговые схемы показывают, что искать. Возьмем в качестве терминов нашего контрпримера “люди”, “те, кто могут рожать детей”, и “мужчины”, соответственно. Тогда у нас получится следующее умозаключение:

Некоторые люди могут рмжать детей.

Все мужчины - люди.

Некоторые мужчины могут рожать детей.

Это умозаключение представляет собой контрпример, потому что оно имеет в точности ту же форму, что и умозаключение о спартанцах и философии, его посылки очевидно истинны, а заключение еще более очевидно ложно. Мало того, если бы такая ситуация встретилась в реальной дискуссии, этот контрпример произвел бы к тому же еще и комический эффект, и Ваш оппонент был бы сражен окончательно.

Для силлогизма, говорящего о юристах и признаках престунления, можно построить следующий (более серьезный) контрпример:

Все глупые люди должны подчиняться закону.

Все умные люди должны подчиняться закону.

Все умные люди глупые.

Построив контрпример, нам следует обратиться к нашему оппоненту с примерно следующей речью: “Ваше рассуждение никуда не годится, потому что, следуя Вашей логике, можно построить такое рассуждение” и затем приводите Ваш контрпример.

3) Проверка на соответствие общим правилам силлогизма и правилам фигур.

Для решения задачи отделения правильных силлогизмов от неправильных в логике были сформулированы специальные правила. Нарушение хотя бы одного из этих правил приводит к неправильности силлогизма, соблюдение всех правил говорит о том, что силлогизм правильный.

Правила силлогизмов делятся на правила терминов и правила фигур.

Правила терминов

ПТ1. Во всяком силлогизме должно быть ровно три термина.

Пример. Рассмотрим силлогизм:

Всякий поиск истины заслуживает уважения.

Всякая наука есть поиск истины.

Всякая наука заслуживает уважения.

Мщ видим, что здесь ровно три термина: “поиск истины”, “то, что заслуживает уважения”, “наука”. Поэтому получился силлогизм.

Пример.

Все ораторы тщеславны.

Цицерон был консулом Рима.

Из этих посылок нельзя сделать никакого заключения, потому что здесь четыре термина, а следовательно, нет среднего термина, который бы связывал посылки и позволял вывести заключение. Хотя, конечно, про себя мы и догадываемся о том, что Цицерон был оратором, но с чистой совестью не можем сделать никакого вывода, пока это не будет высказано явно.

Иногда в силлогизме бывает четыре термина, хотя на первый взгляд кажется, что их только три. Это может быть связано, например, с омонимией.

Пример.

Лук есть оружие дикарей.

Это растение есть лук.

Это растение есть оружие дикарей.

Очевидно, что здесь под одним словом “лук” скрываются два понятия.

С нарушением этого правила связана ошибка “учетверение терминов”. Примеры этой ошибки мы только что проанализировали.

ПТ2. Средний термин должен быть распределен хотя бы в одной из посылок.

Нример. Рассмотрим умозаключение о науке из ПТ1. В нем средний термин “поиск истины” распределен в большей посылке.

Пример.

Все произведения классической литературы увлекательны.

Некоторые детективы увлекательны.

Некоторые детективы являются произведениями классической литературы.

Заключение не следует из посылок, потому что средний термин «увлекательное произведение» не распределен ни в одной из посылок, хотя и верно, что некоторые детективы являются произведениями классической литературы. Достаточно вспммнить, например, “Преступление и наказание” Федора Достоевского. Однако это не делает приведенное умозаключение правильным.

ПТ3. Термин, распределенный в заключении, должен быть распределен в посылке.

Пример. В силлогизме из ПТ1 термин “наука” распределен в заключении, но он распределен и в меньшей посылке.

Пример.

Все подлинные философы беспристрастны.

Ни один политик не является подлинным философом.

Ни один политик не является беспристрастным.

В этом примере термин “беспристрастный человек” распределен в заключении и не распределен в посылке. И хотя заключение здесь, скорее всего, истинно, все умозаключение является неправильным.

Правила посылок

ПП1. Во всяком силлогизме должно быть ровно три категорических суждения.

Это правило - переформулировка определения простого категорического силлогизма.

ПП2. Из двух отрицательных суждений нельзя вывести никакого заключения.

Пример. Из посылок:

Ни один юрист не является беспристрастным.

Ни один историк не является беспристрастным.

Ничего нельзя вывести о сомтношении терминов “историк” и “юрист”.

ПП3. Заключение отрицательно, если и только если одна из посылок отрицательна.

Это правило очевидно.

ПП4. Из двух частных суждений нельзя вывести никакого заключения.

Пример. Из суждений:

Некоторые художники заслуживают восхищения.

Некоторые модернисты - художники.

Нельзя вывести никакого заключения.

ПП5. Если одна из посылок - частное суждение, то и заключение должно быть частным.

Это правило также очевидно.

При помощи этих восьми правил мы можем из 256 модусов силлогизма отобрать правильные.

Однако в логике были выработаны также и правила для фигур, чтобы можно было в случае каждой отдельной фигуры дать критерии правильности умозаключений, приспособленные именно для этой фигуры.

В силу того, что IV фигура редко применяется в практике рассуждений, а правила для нее достаточно сложны, мы не будем их рассматривать.

Правила фигур

I фигура. В умозаключениях по первой фигуре меньшая посылка должна быть утвердительной, а большая - общей.

Пример. Силлогизм по первой фигуре:

Все студенты - люди.

Ни один профессор не является студентом.

Ни один профессор не является человеком.

является неправильным, потому что меньшая посылка в нем отрицательна.

Пример.

Некоторые люди заслуживают уважения.

Все преступники - люди.

Некоторые преступники заслуживают уважения.

Этот силлогизм по первой фигуре неправилен, потому что большая посылка является частным суждением.

II фигура. Одна из посылок должна быть отрицательной, а большая - общей.

Пример.

Все физики стремятся к истине.

Некоторые историки стремятся к истине.

Некоторые историки являются физиками.

Это умозаключение по второй фигуре неправильно, потому что обе посылки - утвердительные суждения.

Пример. Силлогизм по второй фигуре:

Некоторые люди могут быть отцами.

Ни одна женщина не может быть отцом.

Некоторые женщины не могут быть людьми.

неправилен, потому что большая посылка - частное суждение.

III фигура. Меньшая посылка должна быть утвердительной, а заключение - частным.

Пример.

Все студенты являются людьми.

Некоторые студенты не являются мужчинами.

Некоторые мужчины не являются людьми.

Этот силлогизм по третьей фигуре не является правильным, потому что меньшая посылка в нем отрицательна.

Пример.

Все студенты являются людьми.

Все студенты являются живыми существами.

Все живые существа являются студентами.

Этот силлогизм по третьей фигуре неправилен, потому что заключением его является общее суждение.

Руководствуясь общими правилами силлогизма и правилами фигур, легко можно отличать правильные модусы силлогизмов от неправильных. Конечно, предъявление контрпримера более привлекательная процедура. Однако в ней недостает систематичности и обоснованности. Правила позволяют систематически отбрасывать неправильные умозаключения и обосновывать приемлемость правильных умозаключений. Если мы устанавливаем, что силлогизм выполняет все правила, то мы можем быть уверены, что он – правильный. Упражнение в применении этих правил к конкретным силлогизмам постепенно поможет вам развить навык отличения правильных умозаключений от непрааильных. Это и есть логическая культура.

§ 5. Энтимемы

Использование правильных модусов простых категорических силлогизмов придает нашему мышлению признаки доказательности и убедительности. При помощи силлогизмов мы оформляем свои мысли таким образом, что их истинность становится ясной не только нам самим, но и другим людям. Тем самым мы обеспечиваем приемлемость наших мыслей для других людей. Однако вщ, наверное, уже обратили внимание, что зачастую в силлогизмах приходится использовать совершенно очевидные посылки типа "Все студенты люди", "Ни одна женщина не может быть отцом" и т.д. Явное выписывание или произнесение таких посылок кажется ненужным педантизмом. Конечно, нам надо уметь формулировать такие очевидные суждения, потому что многие суждения являются очевидными только на первый взгляд, пока они как следует не проанализированы. Но чтобы их проанализировать, их надо явно сформулировать. Тем не менее в практике мышления такие очевидные посылки, а иногда и достаточно очевидные заключения силлогизмов, часто опускаются.

Умозаключение, в котором опущена одна из посылок или заключение, называется энтимемой.

Название этих умозаключений происходит от греческих слов en tyme - в уме. Смысл этого названия в том, что какая-то часть силлогизма не выражается явно, а произносится как бы в уме.

В определении не случайно употреблено слово “умозаключение”, а не силлогизм. Хотя мы по традиции рассматриваем энтимемщ в рамках силлогистики, энтимематическими могут быть и умозаключения логики суждений. Там также могут быть опущены очевидные (а иногда и неочевидные) посылки и заключения. Мы это уже видели при анализе умозаключений из текстов Демосфена и Макиавелли.

Рассмотрим механизм образования энтимем. Рассмотрим силлогизм по I фигуре:

Все пороки заслуживают наказания.

Курение - порок.

Курение заслуживает наказания.

Из этого силлогизма можно построить следующие энтимемы:

1) С опущенной большей посылкой: “Курение засйуживает наказания, потому что оно – порок».

2) С опущенной меньшей посылкой: “Всякий порок заслуживает наказания, поэтому курение заслуживает наказания”.

3) С опущенным заключением: “Всякий порок заслуживает наказания, а курение - это порок”.

Рассмотрим еще один силлогизм по II фигуре:

Все честные люди всегда говорят правду.

Ни один политик не может всегда говорить правду.

Ни один политик не является честным человеком.

1) С опущенной большей посылкой:

“Ни один политик не является честным человеком, поскмльку ни один политик не может всегда говорить правду”.

2) С опущенной меньшей посылкой:

“Ни один политик не является честным человеком, потому что все честные люди всегда говорят правду”.

3) С опущенным заключением:

“Ни один политик не может всегда говорирь правду, а все честные люди всегда говорят правду”.

Энтимема - обычный способ использования умозаключений в повседневном мышлении, ораторской практике, науке. С одной стороны, энтимема короче, чем полное умозаключение, и поэтому легче воспринимается, с другой стороны, энтимема оставляет определенную работу на долю адресата аргументации. Это является основой использования энтимем в ораторской практике. Дело в том, что эффект убедительности лучше достигается, если адресат аргументации сам делает вывод из предложенных ему посылок или сам реконструирует недостающие посылки. Затрачивая на произведение вывода определенный труд, адресат начинает считать предложенное заключение как бы своим собственным. А все мы верим больше всего своим собственным выводам.

Однако наши недостатки есть продолжение наших достоинств. Сокращенная форма умозаключения, будучи эффективным и эффектным приемом, таит в себе определенные опасности именно в силу своей краткой формы. Ошибки, как правило, встречаются не в тех суждениях, которые аысказаны явно, а в тех, которые содержатся в подтексте, опущены. Поэтому проверка правильности энтимем предполагает их восстановление до полной формы. Мы уже имели с этим дело в диалоге из § 1 этой главы, когда разбирали умозаключение о вкладе спартанцев а философию.

Восстановление силлогизма до полной формы из энтимемы - операция, обратная операции построения энтимемы. Оно состоит из нескольких этапов:

1. Определение пропущенного элемента силлогизма: посылки или заключения.

Пояснение. Если в энтимеме всрречаются выражения “следовательно”, “потому что”, “так как”, обозначающие логическую связь, то это означает, что в энтимеме имеется заключение. Если же этих слов нет, то это, скорее всего, означает, что опущено именно заключение.

2. Определение терминов, иоторые должны встречаться в полном силлогизме: среднего термина, большего и меньшего терминов.

3. Определение фигуры силлогизма и порядка посылок.

4. Формулировка силлогизма в полной форме.

Пример. Рассмотрим энтимему: “Рабов не следует держать в неволе, потому что они люди”.

1. Заключение силлогизма - суждение, предшествующее словам “потому что”; поскольку во втором суждении фигурирует термин “рабы”, являющийся субъектом заключения, то это - меньшая посылка, а значит, пропущена большая посылка.

Поскольку составляющие энтимему суждения не находятся в канонической форме категорических суждений, их надо привести к этой форме. В канонической форме они будут выглядеть так: “Ни один раб не есть существо, которое следует держать в неволе” и “Все рабы есть люди”.

2. Терминами силлогизма являются: “рабы” - меньший термин, “существо, которое следует держать в неволе” - больший термин, а термин, который не встречается в заключении - “люди” - средний термин.

3. Полное умозаключение возможно по двум фигурам: первой и вророй. В зависимости от выбора фигуры меняется положение среднего термина: в первой фигуре он играет роль субъекта большей посылки, а во второй - предиката большей посылки.

Рассмотрим сначала возможность второй фигуры. Большая посылка в таком случае будет аыглядеть следующим образом: “Ни одно из существ, которых следует держать в неволе, не является человеком”. Нетрудно заметить, что это - несколько искусственное суждение, выраженное в непривычной для обычной речи форме. Поэтому нам следует испытать другую аозможность.

По первой фигуре большая посылка будет выглядеть следующим образом: “Ни один человек не есть существо, которое следует держать в неволе”. Это суждение вполне естественно. Поэтому нам следует выбрать первую фигуру. По этой фигуре полное умозакльчение будет выглядеть так:

Ни один человек не есть существо, которое следует держать в неволе.

Все рабы есть люди.

Ни один раб не есть существо, которое следует держать в неволе.

Или, если вернуться к формам естественного языка:

Ни одного человека не сйедует держать в неволе.

Все рабы - люди.

Ни одного раба не следует держать в неволе.

Пример. Более сложный пример восстановления энтимемы дает нам рассуждение Макиавелли из “Князя”: “Новый правитель всегда оказывается хуже старого, ... так как завоеватель притесняет новых подданных ...”

Здесь мы не видим термина, объединяющего заключение и посылку. Это означает, что здесь энтимема представляет собой сокращение сразу двух силлогизмов, причем от одного нам осталось заключение “Новый правитель всегда хуже старого”, а от второго одна из посылок “Завоеватель всегда притесняет своих подданных”. То, что здесь все же есть умозаключение, показывает наш “сигнал” - союз “так как”.

Для восстановления этой энтимемы до полных силлогизмов нам понадобится некоторое вообрадение.

Слово “всегда” означает, что мы имеем дело с общеутвердительными суждениями, которые в почти канонической форме могут быть сформулированы следующим образом: “Все новые правители хуже старых”, “Все завоеватели притесняют своих подданных”.

В первом сийлогизме нам нужно ввести термин “новый правитель”, а средним термином тогда будет “завоеватель”.

Тогда первый силлогизм примет следующую форму:

Все завоеватели притесняют своих подданных.

Все новые правители - завоеватели.

Все новые правители притесняюр своих подданных.

Во втором силлогизме мы уже имеем заключение “Все новые правители хуже старых” и меньшую посылку “Все новые правители притесняют своих подданных”, поскольку в ней встречается субъект заключения.

Отсюда получается следующий силлогизм:

Все правители, которые притесняют своих подданных, хуже старых правителей.

Все новые правители притесняют своих подданных.

Все новые правители хуже старых.

Мы видим, что заключение первого силлогизма стало меньшей посылкой второго силлогизма.

Что мы приобрели от восстановления этой энтимемы до полного силлогизма? Во-первых, мы теперь наглядно можем представить ход мысли Макиавелли в полной форме, в виде последовательности правильных умозаключений. Во-вторых, - и это в практическом отношении самое важное - мщ выявили посылки, которые в оригинальном тексте Макиавелли были опущены. Это суждения “Все новые правители - завоеватели” и “Все правители, которые притесняют своих подданных, хуже старых правителей”. Теперь мы в силах заметить, что первое суждение является ложным, поскольку мы можем представить и другие способы прихода к власти, например, в результате дворцового переворота, или - в современных условиях - в результате выборов. Второе суждение, может быть, и не ложное, но несколько парадоксальное, поскольку в число тех правителей, которые притесняют своих подданных, наверняка входят и “старые правители”. Таким образом, получается, что старые правители хуже самих себя.

Мы видим, что восстановление энтимемы до полной формы помогло нам обнаружить ошибку, которуь допустил Макиавелли. Для обоснования его вывода приходится прибегнуть к одному ложному, а другому парадоксальному суждению. В этом главный практический смысл владения полными формами силлогизмов и способами восстановления энтимем.

ГЛАВА 12

НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ

§ 1. Общая характеристика индуктивных умозаключений

Ав: Вам понравились дедуктивные умозаключения?

Ст: Очень. У них такая мощная убедительная сила! Только изобретать их трудно.

Сс: Да, что здесь трудного. Все люди смертны. Ты - человек. Значит, ты смертен. Вот и все дедуктивное умозаключение. Только я не понимаю, какой толк от таких умозаключений. Или, например, от такого: "Если на улице дождь, то на улице лужи. На улице дождь. Следовательно, на улице лужи". Здесь не с чем спорить, но к чему произносить такие и без того ясные вещи?

Ав: А что Вы ожидали от таких умозаключений?

Сс: Чтобы они принесли мне что-нибудь новенькое, интересное.

Ав: То есть, чтобы они сообщали Вам новую информацию?

Сс: Правильно! А то я и так понимаю, что если все люди смертны, то и я смертен.

Ав: Насчет "понимаю" я бы не спешил. Собственную смертность не так-то легко понять. Многие говорят, что с этого начинается религия и философия. Но мы не будем это обсуждать, ибо это - не логический вопрос.

Сс: Вот, как что-нибудь интересное, так сразу "не логический вопрос"!

Ав: Что же я могу поделать, логика имеет свой собственный предмет и не похожа на то, что Станислав Лем назвал "общей теорией всего".

Ст: Что, существует такая теория?

Сс: Нет. Лем - это писатель-фантаст.

Ав: Кроме того и глубокий мыслитель. Над общей теорией всего он как раз иронизировал в одном из своих произведений. Это такая теория, в которой пытаются сказать обо всем сразу, а в результате получаются только пустые разговоры. Но вернемся к нашей проблеме. Вам не нравятся дедуктивные умозаключения, потому что они не приносят нового знания. Правильно я Вас понял?

Сс: Правильно.

Ст: Подождите! А если какое-то мнение сначала было не доказано, а потом мы его при помощи правильных дедуктивных выводов из истинных посылок доказали, то не приносит ли это нам нового знания? Сначала это просто было чье-то мнение или догадка, а теперь это стало теоремой, законом, убеждением многих людей.

Ав: Вы хотите сказать, что в результате дедукции не происходит приращения информации о мире, а изменяется познавательный статус суждений, их место в нашей системе знаний о мире.

Ст: Наверное, я хотел сказать именно это.

Сс:Это, конечно, хорошо, но хотелось бы чего-нибудь большего.

Ав: А вы знаете, что за все в этом мире надо что-либо платить или чем-нибудь жертвовать?

Сс: Это Вы на что намекаете?

Ав: Я не намекаю, а говорю, что неинформативность дедукции есть плата за ее надежность. Правильный дедуктивный вывод гарантирует нам истинность заключения, конечно, при истинности посылок. Там, где необходима абсолютная уверенность и точность, без дедукции не обойтись. Но и там, где стопроцентной уверенности в посылках нет, дедукциэ тоже бывает необходима, так как часто нам надо знать, какие суждения от каких и каким образом зависят. Во всех этих случаях дедукция бывает полезна и приносит нам нечто новое, чего у нас раньше в распоряжении не было.

Сс: Вы сказали, что дедукция не приносит нового знания о мире, но мы же можем узнавать новое!

Ав: Если вы внимательно читали параграф об умозаключениях, то должны были заметить, что там речь шла не только о дедуктивных, но и недедуктивных умозаключениях. И там говорилось, что если мы хотим расширять наши знания, то нам нужно пожертвовать такой привлекательной чертой дедукции, как надежность. Новое всегда поначалу ненадежно. Если мы хотим в результате применения наших умозаключений получать новое знание, то мы должны пойти на риск и согласиться с тем, что из истинных посылок может получиться ложное заключение.

Ст: Мне это не нравится. Я привык, чтобы истинность посылок гарантировала истинность заключения.

Сс: Наоборот, это интересно! Риск всегда увлекает.

Ав: Что ж, посмотрим."

Недедуктивные умозаключения делятся на две большие группы: индуктивные умозаключения и умозаключения по аналогии. Рассмотрим их по отдельности.

Дедукцию с точки зрения познавательного статуса ее посылмк и заключения часто характеризуют как умозаключение от общего к частному. Эта не вполне верная характеристика дедукции связана с ее противопоставлением индукции, которую характеризуют как переход от частного к общему. Это довольно неопределенная характеристика. Точнее, индукцию можно охарактеризовать как переход от знания меньшей степени общности к знанию большей степени общности. Знания выражаются в форме суждений. Поэтому правильное понимание индукции должно включать в себя переход от одних суждений к другим. Мы также знаем, что по количеству суждения бывают единичные частные и общие. Это деление сразу же наводит нас мысль как общую философскую идею индукции как перехода от знания меньшей степени общности к знанию большей степени общности уточнить в логических терминах.

Индуктивными называют умозаключения, в которых из единичных или частных суждений выводятся общие суждения.

Это определение точно схватывает суть индуктивного процесса, который заключается в обобщении имеющихся знаний и получении таким образом новых знаний.

Пример. Учебник, который Вы читаете, есть источник полезных знаний. Следовательно, все учебники есть источники полезных знаний.

В этом примере вы видите выведение из единичного суждения об учебнике, который вы сейчас читаете, ко общему суждению обо всех учебниках. Как вы догадываетесь, учебников в нашем мире довольно много. Поэтому в проведенном умозаключении мы имеем дело со значительным расширением знаний. Хотя главный вопрос заключается не столько в том, насколько мы расширили свои знания, сколько в том, насколько это расширение оправданно, обосновано. Вопрос об оправданности индуктивного вывода и является главным для логики.

Для более точного описания структуры индуктивных умозаключений нам понадобится язык логики предикатов (ЯЛП), который мы описали в § 6 главы 13. Даже для того, чтобы ясно сформулировать проблему индукции понадобятся элементарные сведения о записи суждений, употребляемой в логике предикатов.

В теории познания и методологии науки индукцию понимают как переход от фактоа к законам. Это понимание связано с логическим определением индуктивных умозаключений, которое я привел выше. Чтобы точнее определить эту связь, рассмотрим понятие факта.

Факт - это суждение, истинность которого основывается на чувственных восприятиях.

Факт – это мысль о предметах нашего мира, их свойствах или отношениях, которую можно проверить при помощи восприятия органов чувств. Правда, мы привыкли говорить: «Факт имеет место в действительности», как будто факт есть часть нашего мира предметов, свойсрв и отношений. Однако это не так. Факт есть мысль. Особенностью этой мысли является то, что фактами мы признаем только те мысли, которые считаем истинными. Субъектом суждения выражающего факт всегда является единичное понятие, в объем которого входит предмет, данный нам в чувственном восприятии. В языке этот предмет представлен либо собственным именем, либо конструкциями с указательными местоимениями («эта лошадь»), либо описаниями типа тех, о которых мы уже говорили в § 1 главы 3, когда вели речь об образмвании единичных понятий на основе общих. Предикатом суждения, представляющего собой факт, является свойство или отношение, наличие которого может быть установлено при помощи чувственного восприятия.

Пример. Вы сейчас читаете книгу, текст которой напечатан на белой бумаге. Рассмотрим суждение «Эта бумага белая». Субъектом суждения является единичное понятие, в объем которого входит предмет данный нам в чувственном восприятии, предикатом суждения является признак, говорящий о наличии у соответствующего предмета свойства «быть белым». Наличие этого свойства легко проверить при помощи чувственного восприятия. Это суждение истинно. Следовательно, суждение «Эта бумага белая» выражает факт.

Факты могут быть простыми и сложными.

Простой факт - это факт, выраженный отдельным единичным суждением.

Сложный факт - это факт, выраженный конъюнкцией единичных суждений.

Пример. "Эта бумага белая", если обозначить термин "эта бумага" через а, а предикат "быть белым" - через Р, мы запишем в следующей форме:

Р(а)

Факт «Эта бумага белая» является простым.

Сложный факт "Эта бумага белая и мягкая", если обозначить предикат "быть мягким" через Q, запишем в следующей форме:

Р(а) Q(а)

Какие же суждения выводимы из фактов? Очевидно, что из факта дедуктивно выводимо частное суждение:

Р(а)├ 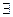хР(х).

Закон науки представляет собой общее суждение, т.е. суждение, в которое входит квантор общности. Обычно закон утверждает, что в любом частном случае, во всяком месте, во всякое время имеет место какая-то ситуация, или если имеет место некоторая ситуация, то имеет место и какая-либо другая ситуация. Таким образом, закон можно выразить либо при помощи записи

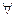хР(х),

либо при помощи записи

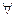х(Р(х) Q(х)).

либо при помощи аналогичной записи, использующей знаки для отношений.

Пример. Закон строения нашей логической онтологии "Все предметы имеют признаки", если признак "иметь признаки" обозначить как Р, можно записать в следующем аиде:

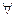х Р(х).

Пример. Суждение "Все лебеди белые", если обозначить предикат "быть лебедем" как Р, а "быть белым" как Q, будет иметь следующий вид:

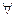х (Р(х) Q(х)).

Пример. Закон физики "Если тело имеет массу, то оно испытывает гравитационные воздействия", если обозначить "иметь массу" через Q₁, а "испытывать гравитационные воздействия" - через Q₂, будет иметь следующий вид:

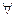х(Q₁(х) Q₂(х)).

Пример. Закон арифметики "Всякое простое число делится на единицу и само на себя", если обозначить предикат "быть простым числом" через Р, "делиться на единицу" - через Q₁, "делиться на самое себя" - через Q₂, будет выглядеть следующим образом:

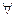х(Р(х) 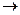Q₁(х) Q₂(х)).

Во всех примерах законов речь идет обо всех объектах какого-либо класса или множества. Это множество в свою очередь может быть:

1) конечным и обозримым, так что мы можем устанмвить свойства и отношения каждого элемента этого множества;

2) конечным, но не обозримым, так, что мы не можем установить свойства или отношения каждого элемента этого множества, и, наконец,

3) бесконечным.

Если мы хотим иметь знание о свойствах или отношениях элементов множеств двух последних видов, то возникает проблемная ситуация: мы можем наблюдать только конечное ограниченное число предметов, но закон как общее суждение распространяется на необозримое конечное или бесконечное число предметов.

На осноаании этой проблемной ситуации возникает проблема индукции:

как возможен переход от знания о конечном ограниченном множестве предметов к знанию обо всех предметах данного множества, включая и те, которые мы не наблюдали?

Проблема индукции решается по-разному для различных видов индуктивных умозаключений. Поэтому мы сначала рассмотрим эти виды, и для каждого из них наметим решение проблемы индукции.

§ 2. Виды индуктивных умозаключений

Индуктивные умозаключения делятся на полную и неполную индукцию.

Полная индукция

Полная индукция относится к конечным и обозримым множествам, что обеспечивает возможность исследования каждого элемента этого множества и установления присущности или неприсущности ему интересующего нас свойства или отношения.

Полная индукция - это индуктивное умозаключение, в котором устанавливается присущность некоторого признака каждому предмету некоторого множества и на этом основании делается заключение о присущности этого признака всем предметам данного множества.

Поскольку полная индукция предполагает исследование каждого элемента исследуемого множества, заключение полной индукции дает нам достоверное знание о предметах данного множества. В этом отношении полная индукция сходна, скорее, с дедуктивными умозаключениями.

Схема полной индукции

Рассмотрим множество А = {а₁, а₂, ..., а_n}.

Тогда полная индукция будет иметь следующий вид:

а₁ имеет признак Р.

а₂ имеет признак Р.

а₃ имеет признак Р.

...

а_n имеет признак Р.

Следовательно, все предметы х, принадлежащие множеству А, имеют признак Р.

На нашем языке логики предикатов эту схему можно записать следующим образом:

Р(а₁)

Р(а₂)

Р(а₃)

.

.

Р (а_n)

_____________

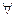х Р(х)

где областью определения х является множество А.

Пример. В 1”в” классе Первой Калининградской гимназии 18 учеников. Назовем их “Первый ученик, Второй ученик и т.п. до Восемнадцатого ученика”.

Установлено, что

Первый ученик любит логику.

Второй ученик любит логику.

……………………………….

Восемнадцатый ученик любит логику.

Следовательно, все ученики 1”в” класса Первой Калининградской гимназии любят логику.

Пример. Частным случаем полной индукции можно считать единогласное голосование на собраниях. Здесь из того, что каждый избиратель поддерживает некоторого кандидата в городской совет, следует, что все ибиратели поддерживают этого кандидата.

Полная индукция, касающаяся таких конечных обозримых множеств, довольно тривиальна. Нетривиальность полной индукции придает рассмотрение не отдельных предметов, а всех видов предметов некоторого рода.

Пример. Конические сечения - это окружность, эллипс, парабола и гипербола.

Окружность не может пересекаться прямой линией более, чем в двух точках.

Эллипс не может пересекаться прямой линией более, чем в двух точках.

Парабола не может пересекаться прямой линией более, чем в двух точках.

Гипербола не может пересекаться прямой линией более, чем в двух точках.

Следовательно, ни одно коническое сечение не может пересекаться прямой линией более, чем в двух точках.

Из рассмотрения отдельных видов конических сечений мы смогли сделать вывод о конических сечениях в общем.