Правило соразмерности.

Объединение объемов членов деления должно совпадать с объемом делимого понятия.

Мы с вами помним, что объединение[25] — это теоретико-множественная операция, аналогичная арифметической операции сложения.

Пусть A — объем делимого понятия, а B1, B2, ... Bn— все члены деления. Тогда на языке теории множеств это правило может быть записано следующим образом:

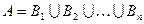
Это правило говорит о том, что при делении

а) не должно быть пропущено ни одного предмета из объема делимого понятия

и

б) не должно появиться ни одного лишнего предмета.

В соответствии с этим различаются два типа возможных ошибок, возникающих при нарушении требования соразмерности:

а) Неполнме деление.

Деление называется неполным, если объединение членов деления является частью объема делимого понятия.

Другими словами, эту ошибку можно охарактеризовать так:

Деление является неполным, если среди членов деления не достает какого-либо вида предметов, выделяемого по данному признаку.

На теоретико-множественном языке эту ошибку можно охарактеризовать следующим образом:

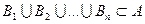
Пример. Если мы среди всех книг выделим художественные и научные, то это будет неполное деление, поскольку явно пропущен еще один вид книг — учебные.

Пример. Если среди всех юридических фактов выделяются правообразующие и правопрекращающие, то это также будет неполное деление, поскольку пропущен еще один вид юридических фактов — правоизменяющие.

б) Обширное деление.

Обширным называется деление, при котором объем делимого понятия является частью объединения объемов членов деления.

Другими словами, деление будет обширным, если среди членов деления встретится понятие, в объем которого входят объекты, не входэщие в объем делимого понятия.

На теоретико-множественном языке эту ошибку можно охарактеризовать следующим образом:

.

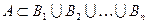Пример. Предложения бывают повествовательные, побудительные, вопросительные и незаконченные.

Это — обширное деление, поскольку первые три члена деления представляют собой различные виды предложений в зависимости от целей говорящего, а последний член деления — незаконченные предложения — вообще предложением не является, ибо предложение выражает законченную мысль, а незаионченные предложения законченной мысли не выражают. Иначе говоря, это деление выводит нас за пределы объема понятия «предложение» и поэтому представляет собой слишком обширное деление.