Основна теорема арифметики цілих невід’ємних чисел.

5. Основну теорему арифметики називають також теоремою про існування та єдиність розкладу будь-якого натурального числа на добуток простих множників. Ця теорема використовувалась ще у стародавній Греції, але була сформульована і доведена видатним німецьким математиком К.Гауссом у 1801 році.

Теорема: будь-яке, більше за одиницю, натуральне число а, або просте, або може бути однозначно розкладене в добуток простих чисел з точністю до порядку розміщення співмножників.

Доведення: доведення складається з двох частин. У першій частині доведемо існування такого розкладу. Якщо аєN і a>1, то можливі два випадки : а) число а – просте, тоді розклад існує; б) число а – складене, тоді воно має найменший простий дільник. Нехай це буде число р₁. Виходячи із цього, маємо а р₁ і а=р₁b, де bєN, причому число 1<р₁< b.

Число b може бути або простим, або складеним. Якщо число b – просте, то ми вже можемо представити число а у вигляді добутку двох простих чисел рb, тобто розклад існує. Якщо b – складене число, то воно має простий дільник. Нехай це буде число р₂. Виходячи із цього, маємо а р₂ і а=р₁р₂с, де сєN, причому число 1<р₂<с. Отже, а=р₁·р₂·с. Знову число с може бути або простим, або складеним. Якщо число с – просте, то число а буде представлятися у вигляді добутку трьох простих чисел. Якщо число c – складене, то ми одержимо ще один простий дільник р₃. Оскільки с< b<а, то цей процес завжди буде закінчуватися, а тому завжди буде існувати розклад числа а у вигляді добутку простих множників 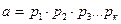(І).

Не виключеним є випадок, коли деякий із множників в розкладі (1) повторюється, а тому в загальному випадку розклад числа на прості множники записують так: 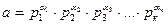(ІІ). Розклад (ІІ) називається канонічним розкладом натурального числа а у добуток простих множників. В цьому розкладі р₁, р₂, р₃,...,р_k – прості множники, розміщені в порядку зростання; a₁, a₂, a₃,...,a_k– це натуральні числа, які показують, скільки разів повторюється той чи інший множник. Існування доведено.

У другій частині доведемо єдиність такого розкладу методом від супротивного, припустивши, що існує два різних розклади у вигляді (І), тобто а=р₁·р₂·р₃·…·р_к (ІІ) і а=q₁·q₂·q₃·…·q_n (III). Врахуємо, що р₁<р₂<р₃<…<р_к і q₁<q₂<q₃<…<q_n. У даних розкладах р_і і q_і – різні, але серед них будуть однакові. Для визначеності припустимо, що p₁¹q₁ i p₁<q₁.

Утворимо нове число b=p₁·q₂·q₃·…·q_n (IV). Легко бачити, що число а в записі (1) ділиться націло на p₁. Оскільки 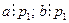, то 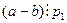. Використовуючи записи (III) і (IV), винесемо добуток q₂·q₃·…·q_n за дужки: (a-b)=(q₁–p₁)·q₂·q₃·...·q_n. Ми показали, що вираз 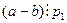. Оскільки р₁ - просте число, то вираз ((q₁-p₁) q₂· q₃· q_n) p₁. Числа q₂, q_3,…q_n - прості і жодне із них не може ділитися на р₁. Тоді на p₁ повинна ділитися різниця (q₁–p₁) р₁. Разом з тим, оскільки р₁ р₁, то 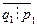, бо p₁¹q₁ і ці числа прості. Отже, для того, щоб (q₁–p₁) р₁ потрібно, щоб q₁-p₁=0, тоді q₁=p₁. Ми прийшли до суперечності із вибором p₁ і q₁. Ця суперечність говорить, що наше припущення про неєдиність розкладу було хибним. Отже, якщо розклад існує, то він єдиний. Теорема доведена повністю.

Доведена теорема є теоретичною основою представлення будь-якого натурального числа у вигляді добутку простих множників. Покажемо це на прикладі такої вправи: „Представити число 1224 у канонічному розкладі, тобто розкласти в добуток простих множників”.

Розв’язання: