Ознаки подільності на складені числа.

8. У математиці, крім поняття простих чисел, широко використовують поняття взаємно-простих чисел.

Означення: два натуральних числа a і b називаються взаємно-простими, якщо їх найбільший спільний дільник дорівнює 1, тобто НСД(а,b)=1.

Теорема 1: якщо натуральні числа a і b взаємно прості, добуток цих чисел ділиться на деяке натуральне число с, а НСД(а,с)=1, то другий співмножник b ділиться на це число с.

Доведення: за умовою НСД(a,c)=1, тоді за властивостями НСК і НСД НСК(а,с)=а·с. Висловлення 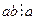істинне за теоремою про подільність добутку. Висловлення 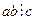істинне за умовою теореми. Тому ab – спільне кратне чисел а і с. За властивостями НСК всяке СК ділиться націло на НСК, тобто 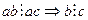. Теорема доведена.

Теорема 2: якщо натуральне число а не ділиться націло на просте число p, то ці числа взаємно прості, тобто НСД(а,p)=1.

Доведення:за умовою aєN, pєNіа p. Оскільки p – просте число, то воно має два дільники: 1 і p. Отже, числа а і p можуть мати не більше двох спільних дільників. Якщо 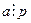, то це б суперечило умові теореми. Отже, числа а і p мають один спільний дільник, яким є одиниця. Отже, НСД(а,p)=1. Теорему доведено.

Теорема 3: якщо добуток кількох натуральних чисел ділиться на просте число p, то принаймні одне із цих чисел ділиться на p.

Доведення: для доведення теореми використаємо метод математичної індукції. Перевіримо справедливість твердження при n=2. Розглянемо добуток двох множників. Тоді за умовою теореми 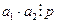. Якщо б 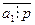, то (за теоремою 2) НСД(а₁,р)=1. Якщо б 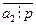, то НСД(а₂,р)=1. Тоді це б суперечило теоремі 1. Отже, наше припущення, про те, що жодне з чисел а₁, а₂ не ділиться на p, було б хибним. Отже, при n=2 теорема справедлива.

Припустимо, що теорема справедлива при n=k, тобто ( 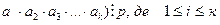. Тоді серед чисел а₁, а₂, а₃…а_к знайдеться принаймні одне число, яке ділиться на p. Нехай .

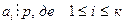Виходячи з припущення спробуємо довести справедливість теореми для n=k+1. Утворимо добуток а₁●а₂●а₃●...а_к●а_к+1. Він являє собою добуток двох співмножників а₁●а₂●а₃●...●а_к і а_к+1. За доведеним в пункті 1: або перший співмножник (а₁●а₂●а₃●...●а_к) або другий а_к+1 ділиться на p. Якщо а_к+1 р, то за теоремою про подільність добутку (а₁●а₂●а₃●...●а_к●а_к+1) р, тобто твердження справедливе при n=k+1. Якщо (а₁●а₂●а₃●...●а_к) р, то серед співмножників знайдеться принаймні один такий, що ділиться націло на просте число р. Отже, і в цьому випадку твердження справедливе при n=k+1. Таким чином, за аксіомою індукції це твердження буде справедливим для довільного натурального числа. Теорему доведено повністю.

Теорема 4: якщо натуральні числа а і b взаємно прості, то для подільності натурального числа с на добуток цих чисел необхідно і достатньо, щоб число с ділилося на кожне з чисел а і b.

Доведення: оскільки в умові теореми є слова необхідно і достатньо, то доведення теореми складатиметься з двох частин. У першій частині слід довести достатню умову: „якщо с ділиться націло на кожне з чисел а і b, то число с ділиться націло на добуток чисел аb”. За умовою с а і с b. Це означає, що число с є спільним кратним чисел а і b. Тоді за властивістю спільного кратного воно поділиться націло на НСК(а,b), тобто с НСК(а,b). Оскільки числа а і b взаємно прості, то НСК(а,b)=аb. Отже, с аb. Достатню умову доведено.

Доведемо необхідну умову: „якщо натуральне число с ділиться націло на добуток взаємно простих чисел аb, то воно ділиться націло на кожне з цих чисел а і b”. За умовою с аb, а за теоремою про подільність добутку аb а. Отже, за властивістю транзитивності відношення подільності с а. Аналогічно, з того, що с аb і аb b, випливає, що с b. Таким чином, необхідну умову доведено. Отже, теорему доведено повністю.

На основі теорем 1–4 формулюються ознаки подільності на складені числа. Щоб сформулювати ознаки подільності на складені числа 6, 12, 15, 18, 22, 36 тощо треба представити їх у вигляді добутку двох взаємно простих чисел. Так, маємо 6=2●3, 12=3●4, 15=3●5, 18=2●9, 22=2●11, 36=4●9. Тепер можна сформулювати ознаки подільності на ці складені числа, а саме:

Для того, щоб натуральне число а ділилося націло на число 6, необхідно і достатньо, щоб воно ділилося націло на кожне з чисел 2 і 3.

Для того, щоб натуральне число а ділилося націло на число 12, необхідно і достатньо, щоб воно ділилося націло на кожне з чисел 3 і 4.

Пропонуємо студентам сформулювати решту ознак самостійно. Таким чином, можна твердити, що в множині натуральних чисел операція ділення виконується не завжди, а тому розрізняють два її види: ділення націло і ділення з остачею. При діленні націло: а:b=q, тобто a=b×q. При діленні з остачею: а=bв×q+r, де r¹0 і 0≤r<b. Якщо зняти це обмеження, тобто вважати, що r може дорівнювати нулю, то обидва види ділення можна звести до одного.

Завдання для самоконтролю та самостійної роботи студентів.

1. З’ясувати, якою достатньою чи необхідною умовою є ознака подільності різниці на число.

2. Сформулювати необхідну і достатню ознаку подільності різниці на це число.

3. Довести теорему про подільність різниці на число аналогічно до теореми про подільність суми на число.

4. З’ясувати, якою ознакою (достатньою, необхідною чи необхідною і достатньою) є теорема про подільність добутку на число.

5. Самостійно довести ознаку подільності на 5.

6. Самостійно довести ознаку подільності на 9.

7. Самостійно довести ознаку подільності на 25.

8. Самостійно довести другу властивість НСК.

9. Сформулювати ознаки подільності на складені числа 15, 18, 22, 26, 36.