Дільники і кратні. Спільні дільники і спільні кратні. Найбільший спільний дільник (НСД) і найменше спільне кратне (НСК), їх властивості.

6.Розглянемо два натуральних числа а та b. Якщо а b, то говорять, що а кратне b.

Означення: якщо а b, то число а називається кратним до числа b.

Із означення відношення подільності відомо, що із а bÛa=b·c. Якщо записати за допомогою характеристичної властивості множину чисел, кратних числу а, то будемо мати множину {a, 2a, 3a, … na…}. У множині чисел, кратних даному числу а є найменше число і немає найбільшого. За допомогою терміна “кратне” задається відношення подільності. Нехай задано множини чисел, кратних числу 3 і числу 5, тобто А={3,6,9,…3n,…} і B={5,10,15,…5n,…}. Утворимо перетин цих множин AÇB={15,30,45,…15n,…}. Множина AÇB задає нам спільні кратні чисел 3 і 5.

Означення: Будь-яке число, кратне числам а₁, а_2, а₃,…,а_n називається спільним кратним цих чисел.

Означення: найменше із спільних кратних чисел а₁, а_2, а₃,…а_k називається найменшим спільним кратним цих чисел.

Найменше спільне кратне прийнято позначати так: НСК(а₁, а₂, а₃,…а_k) або К(а₁, а_2, а₃,…а_k). Розглянемо властивості НСК, сформулювавши відповідні теореми для випадку двох чисел.

Властивість 1: кожне спільне кратне даних чисел ділиться на їх найменше спільне кратне.

Доведення: для спрощення викладок доведення теореми проведемо для випадку двох чисел. Нехай НСК(a,b)=k і CK(a,b)=d. Доведемо, що d k. Доведення проведемо методом від супротивного, припустивши, що 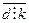, тобто, згідно означення операції ділення з остачею виконуються умови: d=kq+r і 0£r<k. Звідси r=d-kq. Оскільки d є спільним кратним (СК) чисел a і b, то 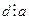. Оскільки k=НСК(a,b), то 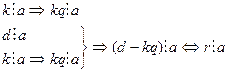. Оскільки r<k, a£ k, то r – ділиться на число, більше, ніж воно саме, тобто число r є спільним кратним чисел a і b. Отже, СК(a,b)=r. А це можливо тоді, коли d–k·q=0, r=0, а це суперечить припущенню, що 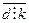. Отже, припущення хибне і теорема доведена.

Властивість 2: якщо НСК(a,b)=k, то для будь-якого сÎN НСК(ac,bc)=ck.

Ця теорема говорить, що будь-який спільний множник можна виносити за знак НСК. Ввівши в попередніх пунктах означення дільника даного числа, ми з’ясували, що кількість дільників є завжди скінченною, найменшим дільником будь-якого числа є 1, а відношення „число b є дільником числа а” є оберненим до відношення „число а кратне числу b”.

Означення: всяке число, на яке ділиться кожне із чисел а₁, а₂, а₃…а_к називається спільним дільником цих чисел.

Означення найбільший із спільних дільників чисел а₁,а₂,а₃…а_к називається найбільшим спільним дільником чисел а₁, а₂, а₃…а_к і позначається НСД(а₁,а₂,а₃…а_к) або Д(а₁,а₂,а₃…а_к).

Означення: числа а₁, а₂, а₃…а_к називаються взаємно простими, якщо їх найбільший спільний дільник дорівнює 1. .

Властивість 1: якщо 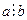, то НСК(a,b)=a, а НСД(a,b)=b.

Доведення: за умовою 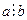і 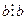, тобто СД(a,b)=b, оскільки a>b, то НСД(a,b)=b. За умовою 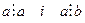, то число а є спільним кратним для чисел a і b. Оскільки a>b, то а=НСК(а, b). Теорема доведена.

Властивість 2: будь-який спільний дільник даних чисел є дільником їх спільного дільника.

Властивість 3: спільні дільники даних чисел можна виносити, як за знак найменшого спільного кратного, так і за знак найбільшого спільного дільника.

Властивість 4: найменше спільне кратне даних чисел дорівнює добутку цих чисел, поділеному на найбільший спільний дільник цих чисел, тобто: .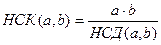

Справедливість властивостей 2-4 приймемо без доведення.