Структурные методы повышения надежности ЭВМ
Значительного повышения надежности ЭВМ достигают созданием новых элементов. Так, применение интегральных схем (ИС) для построения основных узлов ЭВМ (регистров, сумматоров и др.) привело к значительному повышению надежности машин третьего и четвертого поколений. Однако повышение надежности элементов ЭВМ методами, рассмотренными выше, не удается в настоящее время полностью решить эту проблему, что вызвано значительным опережением роста сложности вновь разрабатываемой вычислительной техники, большими затратами при получении элементов высокой надежности, а также существованием элементов, надежность которых довольно низка и трудно поддается повышению (устройства ввода и вывода информации и др.). Поэтому один из путей повышения надежности ЭВМ — введение схемной избыточности.
Разработка методов синтеза ЭВМ, обладающих заданной надежностью, сводится к нахождению оптимальной избыточности. При этом, основное — согласование метода повышения достоверности с наиболее вероятными ошибками, появляющимися в различных устройствах ЭВМ. Полные и достоверные сведения об ошибках могут быть получены при эксплуатации машин, но проведение подобных испытаний связано с большими затратами времени и не всегда возможно при эксплуатации. Кроме того, такие сведения зависят от конкретного конструктивного выполнения ЭВМ и конкретных условий ее эксплуатации, в связи с этим они частично теряют свою ценность при проектировании новых вычислительных устройств. Поэтому на практике сведения об ошибках получают приближенно по результатам специальных статистических испытаний, проводимых на установках, которые содержат испытуемое устройство (контрольное устройство работает так же, как и испытуемое, однако в нем приняты специальные меры по повышению надежности) и устройство автоматической обработки результатов.
При обработке статистических данных определяют вероятностные характеристики ошибок как функции времени работы устройств. К этим характеристикам относят вид распределения, среднее время между отказами или сбоями, кратность ошибок, наличие пачек и др. Эти характеристики являются исходными данными для выбора метода введения избыточности и расчета надежности проектируемой ЭВМ. Так как увеличение надежности отдельных элементов есть предел, обусловливающий современный уровень развития технологии их изготовления, а сложность устройств стремительно возрастает, то введение схемной избыточности имеет все большее значение при построении надежных ЭВМ.
Один из видов схемной избыточности — структурное резервирование, предполагающее включение в схему устройства дополнительных элементов, которые позволяют скомпенсировать отказы отдельных частей устройств и обеспечить его надежную работу. Но резервирование эффективно только в том случае, когда неисправности являются статистически независимыми.
В ЭВМ ввод структурной избыточности производят по следующей схеме: входные сигналы поступают на п логических схем, причем n>k где k — число логических схем в нерезервированной схеме. Выходные сигналы всех п логических схем далее подают на решающий элемент, который согласно функции решения по этим сигналам определяет значения выходных сигналов всей схемы.
Функция решения — правило отображения входных состояний решающего элемента на множество его выходных состояний. Простейший и наиболее распространенный вид функции решения — «закон большинства», или мажоритарный закон. В таком случае решающий элемент обычно называют мажоритарным элементом. Работа мажоритарного элемента состоит в следующем: на входы элемента поступают двоичные сигналы от нечетного количества идентичных элементов; выходной сигнал элемента принимает значение, равное значению, которое принимает большинство входных сигналов. Наиболее широко используют мажоритарные элементы, работающие по закону «2 из 3». В этих элементах значение выходного сигнала равно значению двух одинаковых входных сигналов. Кроме того, известны мажоритарные элементы, работающие по закону «3 из 5», «4 из 7» и т. д. Схема мажоритарного элемента, работающего по закону «2 из 3» и построенного из логических элементов И и ИЛИ, основана на выражении z = x1x2 + x2x3 + x1x3 и имеет вид, изображенный на рис. 6.4.
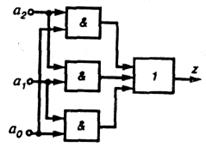
Рисунок 6.4 – Схема мажоритарного элемента «2 из 3»
Вероятность безотказной работы мажоритарной схемы «2 из 3» можно рассчитать по формуле 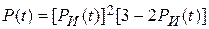 , где
, где 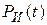 — вероятность безотказной работы схемы И. Вероятность безотказной работы мажоритарной схемы при k = (n-1)/2 определяется соотношением
— вероятность безотказной работы схемы И. Вероятность безотказной работы мажоритарной схемы при k = (n-1)/2 определяется соотношением
 ,
,
где п — число входов мажоритарного элемента;
р — вероятность безотказной работы одного элемента схемы;
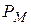 — вероятность безотказной работы мажоритарного элемента.
— вероятность безотказной работы мажоритарного элемента.
Для повышения надежности схемы могут быть введены избыточные мажоритарные элементы. В этом случае при выходе одного или нескольких мажоритарных элементов из строя схема продолжает работать безотказно за счет большинства исправно работающих мажоритарных элементов. Вероятность безотказной работы такой схемы определяется
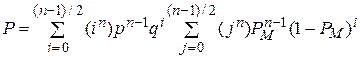 .
.
Однако, если логические схемы не идентичны, «закон большинства» неприменим. В таких случаях используют взвешенные входы решающего элемента. Работу такого решающего элемента описывают пороговой функцией. Функцию алгебры логики F(x1, …, xn) называют пороговой, если существует ряд таких действительных чисел c1, c2, …, cn и Tср для которых выполняется условие
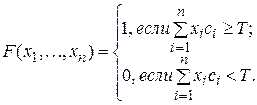
где 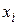 — независимые переменные, принимающие значения 0 или 1;
— независимые переменные, принимающие значения 0 или 1;
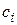 — вес (положительный или отрицательный), соответствующий
— вес (положительный или отрицательный), соответствующий 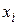 ;
;
Т — порог функции. Наиболее часто в ЭВМ используют пороговые функции, у которых с1 = с2 =…= сn = с > 0 и Т ³ 0. Следовательно,
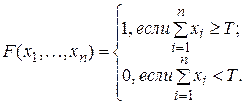
Если (k - 1) < (T/c) £ k, то
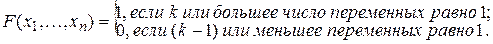
Решающий элемент, работающий согласно этим выражениям, называют пороговым элементом. Схема порогового элемента показана на рис. 6.5. Веса входов порогового элемента выбирают в зависимости от вероятности ошибок в соответствующей логической схеме. Логической схеме с большей вероятностью ошибки соответствует меньший вес, а более надежной схеме — больший вес.
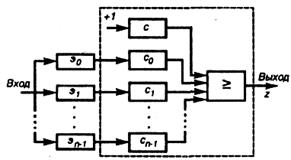
Рисунок 6.5 – Схема порогового элемента
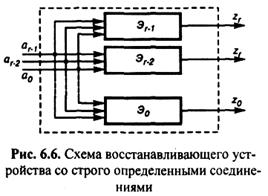
Схемы, преобразующие г избыточных входных сигналов, часть из которых может быть ошибочными, в г безошибочных сигналов, называют восстанавливающими устройствами. Простейший вид восстанавливающего устройства представлен на рис. 6.6. В таких схемах в качестве решающего элемента используют мажоритарный элемент, пороговый элемент и др. Кроме того, имеются устройства, в которых соединение входов выполнено случайным образом. Такие восстанавливающие устройства называют однослойными.
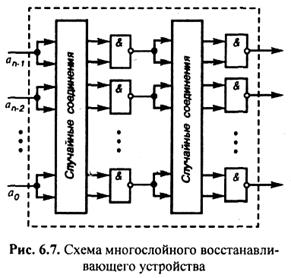
Восстанавливающие устройства могут быть построены также из двух слоев логических элементов с использованием двухвходовых элементов И—НЕ и случайных соединений входов. Схема такого устройства представлена на рис. 6.7. Здесь одиночная ошибка на входе вида  исправляется первым слоем.
исправляется первым слоем.
Одиночная ошибка вида  вызывает двойную ошибку на выходе первого слоя, которая исправляется вторым слоем. Двойная ошибка на выходе первого слоя будет исправлена всегда, когда на каждую пару входов И—НЕ второго слоя поступит хотя бы один безошибочный сигнал. Если на оба входа некоторого элемента И—НЕ поступят ошибочные сигналы, то на выходе восстанавливающего устройства соответствующий сигнал будет ошибочным. При большом г, когда в основном применяют случайные соединения входов, вероятность такого совпадения очень мала. При небольшом г эта вероятность увеличивается и поэтому вместо случайных соединений применяют соединения, соответствующие определенному закону. Законы, определяющие порядок соединения входов, исследуют избыточной логикой с переплетением. Резервирование без восстановления. По способу включения резервных элементов функциональных устройств различают три вида резервирования: постоянное, замещением и скользящее.
вызывает двойную ошибку на выходе первого слоя, которая исправляется вторым слоем. Двойная ошибка на выходе первого слоя будет исправлена всегда, когда на каждую пару входов И—НЕ второго слоя поступит хотя бы один безошибочный сигнал. Если на оба входа некоторого элемента И—НЕ поступят ошибочные сигналы, то на выходе восстанавливающего устройства соответствующий сигнал будет ошибочным. При большом г, когда в основном применяют случайные соединения входов, вероятность такого совпадения очень мала. При небольшом г эта вероятность увеличивается и поэтому вместо случайных соединений применяют соединения, соответствующие определенному закону. Законы, определяющие порядок соединения входов, исследуют избыточной логикой с переплетением. Резервирование без восстановления. По способу включения резервных элементов функциональных устройств различают три вида резервирования: постоянное, замещением и скользящее.
При постоянном резервировании предполагают, что любой отказавший элемент или узел не влияет на выходные сигналы и поэтому его прямого обнаружения не производится. Постоянное резервирование наиболее распространено в невосстанавливаемых устройствах. Кроме того, оно является единственно возможным в устройствах, где недопустим даже кратковременный перерыв в работе. Постоянное резервирование вводится или с помощью решающего блока, или в виде однотипных элементов или блоков, включенных последовательно, параллельно или, например, согласно законам к-краткой логики. В качестве решающего блока можно использовать мажоритарные элементы с постоянными или переменными весами, кодирующие — декодирующие устройства и схемы из логических элементов И, ИЛИ, НЕ.
При резервировании замещением предполагается обнаружение отказавшего элемента или узла и подключения исправного. Замещение может происходить либо автоматически, либо вручную. Резервирование замещением имеет следующие достоинства: для многих схем при включении резервного оборудования не требуется дополнительно регулировать выходные параметры, вследствие того, что электрические режимы в схеме не меняются, резервная аппаратура до момента включения в работу обычно обесточена. Это повышает общую надежность системы за счет сохранения ресурса электронных устройств, кроме того, экономится энергия источников питания, имеется возможность использования одного резервного элемента на несколько рабочих. Из-за сложности аппаратуры для автоматического включения резерва резервирование замещением целесообразно применять к крупным блокам и отдельным функциональным частям ЭВМ.
При скользящем резервировании любой резервный элемент может замещать любой основной элемент. Для осуществления этого резервирования необходимо иметь устройство, которое автоматически находит неисправный элемент и подключает вместо него резервный. Достоинство такого резервирования в том, что при идеальном автоматическом устройстве будет наибольший выигрыш в надежности по сравнению с другими методами резервирования. Однако осуществление скользящего резервирования возможно лишь при однотипности элементов.
Определим основные характеристики надежности ЭВМ при различных видах резервирования. Так как эффективность постоянного резервирования равна эффективности резервирования замещением в нагруженном режиме при идеальных переключателях, полученных характеристик надежности целесообразно провести для резервирования замещением.
Различают резервирование замещением: нагруженное — резервные элементы находятся в таком же рабочем режиме, как и основные элементы; облегченное — резервные элементы находятся в неполном рабочем режиме, непогруженные — резервные элементы находятся в нерабочем состоянии.
Так как время безотказной работы каждой ИС распределено по экспоненциальному закону, а поток отказов простейший, то основа для расчета надежности при различных видах резервирования — вероятность безотказной работы 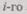 элемента
элемента 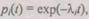 где
где 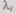 — интенсивность отказа i-го элемента. В случае нагруженного резерва элемент находится в одном и том же режиме и до, и после включения в работу. Поэтому надежность каждого элемента не зависит от моментов отказа других элементов. Можно считать, что время, в течение которого отказавший элемент заменяется резервным, равно нулю.
— интенсивность отказа i-го элемента. В случае нагруженного резерва элемент находится в одном и том же режиме и до, и после включения в работу. Поэтому надежность каждого элемента не зависит от моментов отказа других элементов. Можно считать, что время, в течение которого отказавший элемент заменяется резервным, равно нулю.
Рассмотрим систему из одного основного и т-\ резервных элементов. Введем обозначения:  — вероятности безотказной работы соответствующих элементов в течение времени
— вероятности безотказной работы соответствующих элементов в течение времени 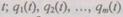 — вероятности отказа;
— вероятности отказа; 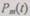 — вероятность безотказной работы всей системы из т элементов;
— вероятность безотказной работы всей системы из т элементов; 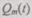 — вероятность отказа всей системы из т элементов. Так как все отказы независимы, то, по теореме умножения вероятностей,
— вероятность отказа всей системы из т элементов. Так как все отказы независимы, то, по теореме умножения вероятностей,

Выражение для надежности имеет следующий вид:
 (6.14)
(6.14)
Если все элементы имеют одинаковую надежность 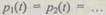
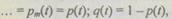 то
то
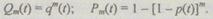 (6.15)
(6.15)
Эти формулы позволяют найти число резервных элементов, при котором  не будет превосходить заданной величины
не будет превосходить заданной величины  Отсюда
Отсюда 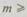
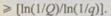 Среднее время наработки на отказ системы
Среднее время наработки на отказ системы
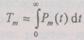
или
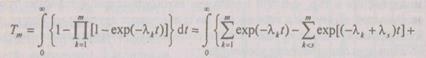
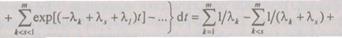
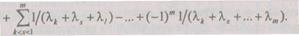 (6.16)
(6.16)
Для случая равных надежностей,  среднее время наработки на отказ системы
среднее время наработки на отказ системы
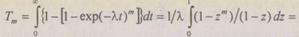
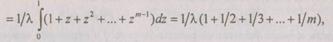 (6.17)
(6.17)
где  Так как среднее время работы одного элемента равно
Так как среднее время работы одного элемента равно  то
то 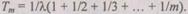
Выражения (6.14) — (6.17) действительны для общего резервирования, когда резервируются блоки, отдельные устройства или целиком ЭВМ. В этом случае под 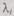 и
и 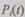 принимается соответственно интенсивность отказов и вероятность безотказной работы
принимается соответственно интенсивность отказов и вероятность безотказной работы 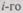 резервированного блока (устройства, ЭВМ). Для случая нагруженного резерва с поэлементным резервированием (рис. 6.8), когда в основном устройстве (блоке, ЭВМ) имеется п элементов, каждый из которых резервируется т - 1 аналогичными элементами, вероятность безотказной работы рассчитывается по формуле
резервированного блока (устройства, ЭВМ). Для случая нагруженного резерва с поэлементным резервированием (рис. 6.8), когда в основном устройстве (блоке, ЭВМ) имеется п элементов, каждый из которых резервируется т - 1 аналогичными элементами, вероятность безотказной работы рассчитывается по формуле
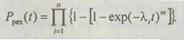 (6.18)
(6.18)
При равнонадежных элементах
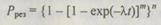
и

где  С точки зрения повышения надежности более эффективно поэлементное резервирование. Параметр т называют кратностью резервирования. Если речь идет, например, о четырехкратном резервировании, то это означает, что в системе имеется один основной элемент и три резервных. При т - 2 наблюдается случай дублирования, а при т = 3 будет тройное резервирование системы.
С точки зрения повышения надежности более эффективно поэлементное резервирование. Параметр т называют кратностью резервирования. Если речь идет, например, о четырехкратном резервировании, то это означает, что в системе имеется один основной элемент и три резервных. При т - 2 наблюдается случай дублирования, а при т = 3 будет тройное резервирование системы.

Пример. Пусть ЭВМ состоит из пяти устройств, отказ любого из которых приводит к отказу всей ЭВМ. Известно, что в данный момент времени 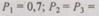
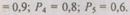 Определить вероятность безотказной работы ЭВМ для случаев: без резерва, с общим резервированием раздельным резервированием. Кратность резервирования т = 3.
Определить вероятность безотказной работы ЭВМ для случаев: без резерва, с общим резервированием раздельным резервированием. Кратность резервирования т = 3.
Для случая без резерва
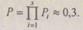
Для случая общего резервирования из (6.15) получим
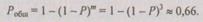
(вероятность времени безотказной работы основного и резервного времени в системе с облегченным резервом).
Для случая раздельного резервирования из (6.18) получим
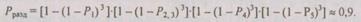
Таким образом, раздельное резервирование в данном примере привело к увеличению параметра надежности почти в три раза, в то время как общее резервирование при тех же аппаратурных затратах увеличило параметр надежности только в два раза.
Рассмотрим случай, когда резервные элементы находятся в неполном рабочем режиме. Пусть система состоит из двух параллельных элементов. Резервный элемент до момента отказа основного элемента находится в облегченных условиях. Плотность распределения времени безотказной работы основного и резервного элементов показана на рис. 6.9.
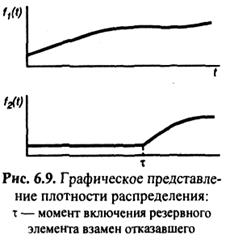
Предполагается, что переключающее устройство действует безотказно. Найдем вероятность безотказной работы системы за время  Обозначим:
Обозначим: 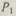 — вероятность безотказной работы основного элемента; kt — интенсивность отказа основного элемента;
— вероятность безотказной работы основного элемента; kt — интенсивность отказа основного элемента;  — вероятность безотказной работы резервного элемента в рабочем режиме;
— вероятность безотказной работы резервного элемента в рабочем режиме; 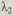 — интенсивность отказа резервного элемента в рабочем режиме;
— интенсивность отказа резервного элемента в рабочем режиме; 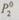 — вероятность безотказной работы резервного элемента в облегченном режиме;
— вероятность безотказной работы резервного элемента в облегченном режиме;  — интенсивность отказа резервного элемента в облегченном режиме.
— интенсивность отказа резервного элемента в облегченном режиме.
Очевидно, что основной элемент имеет два состояния, а резервный — четыре, т. е. общее число всевозможных состояний системы равно восьми. Из этих состояний наиболее благоприятными являются следующие:
а) оба элемента работают безотказно;
б) первый элемент работает безотказно, а второй отказал в интервале времени от 0 до 
в) первый элемент отказал в интервале времени от 0 до  а второй работает безотказно в интервале времени от 0 до
а второй работает безотказно в интервале времени от 0 до  (в облегченном режиме) и в интервале времени от
(в облегченном режиме) и в интервале времени от  до
до  (в рабочем режиме). Вероятность безотказной работы резервированной системы:
(в рабочем режиме). Вероятность безотказной работы резервированной системы:
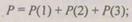

Предположим, что отказ основного элемента в случае (е) произошел на участке от  до
до  Тогда на участке
Тогда на участке 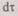 вероятность отказа основного элемента будет
вероятность отказа основного элемента будет  — плотность распределения наработки до отказа основного элемента.
— плотность распределения наработки до отказа основного элемента.
Вероятность Р(3) находят так:
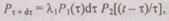
где 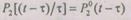 — условная вероятность того, что резервный элемент безотказно проработает время
— условная вероятность того, что резервный элемент безотказно проработает время  при условии, что за время
при условии, что за время  он не отказал. Отказ основного элемента может произойти на любом участке времени Ьт 0 до
он не отказал. Отказ основного элемента может произойти на любом участке времени Ьт 0 до  , поэтому
, поэтому
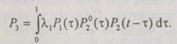
Окончательно
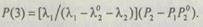
Следовательно, вероятность безотказной работы резервированной системы, состоящей из двух элементов, при условии, что резервный элемент работает в облегченном режиме, равна

Если один элемент основной, а (/и - 1)-е элементы резервные, то вероятность безотказной работы системы, резервированной по способу замещения, равна
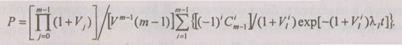
Когда основных элементов к и элементов резервных т - 1, то вероятность безотказной работы системы

При нагруженном режиме плотности распределения времени безотказной работы основного и резервного элементов принимают одинаковыми. В этом случае 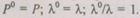 Здесь, если один элемент основной, а
Здесь, если один элемент основной, а  элементы — резервные, то вероятность безотказной работы системы
элементы — резервные, то вероятность безотказной работы системы
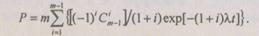
Для  основных элементов и т - 1 элементов резервных
основных элементов и т - 1 элементов резервных
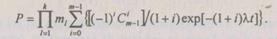
При ненагруженном режиме 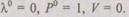 Тогда вероятности безотказной работы систем с резервированием соответственно для случая одного и к основных элементов и т — 1 элементов резервных имеют вид
Тогда вероятности безотказной работы систем с резервированием соответственно для случая одного и к основных элементов и т — 1 элементов резервных имеют вид
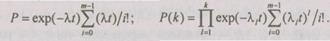
Из трех рассмотренных способов резервирования наибольший выигрыш в надежности получают в ненагруженном режиме. Сравнительный анализ существующих методов и способов резервирования позволяет выбрать лучшие из них. Однако при этом увеличиваются масса, габаритные размеры и стоимость аппаратуры. Поэтому на практике возникает задача резервирования системы, чтобы ее вес, габаритные размеры и стоимость были не выше допустимых значений, а надежность — максимальной или чтобы вероятность безотказной работы была не ниже требуемой, а масса, габаритные размеры и стоимость системы были минимальными. Аналитическое решение этой задачи практически можно получить только для случая поэлементного постоянного резервирования при одном ограничении (при нескольких ограничениях может быть построен алгоритм решения задачи на ЭВМ).
Рассмотрим оптимальное резервирование при ограничении массу аппаратуры (или какой-нибудь одной величины). Пусть имеется нерезервированная система из п последовательных элементов, причем 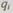 — вероятность отказа
— вероятность отказа  элемента, а
элемента, а  — масса
— масса  элемента. Требуется произвести поэлементное резервирование этой системы так, чтобы ее масса не превышала заданной, а надежность была максимальной. Масса нерезервированной системы и вероятность ее безотказной работы соответственно
элемента. Требуется произвести поэлементное резервирование этой системы так, чтобы ее масса не превышала заданной, а надежность была максимальной. Масса нерезервированной системы и вероятность ее безотказной работы соответственно
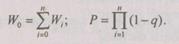 (6.19)
(6.19)
Если каждый элемент зарезервировать т - 1 раз, то масса резервированной системы
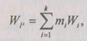
а вероятность исправной работы

Задача сводится к нахождению таких целых чисел  , при которых
, при которых  и масса системы не превышает допустимого значения:
и масса системы не превышает допустимого значения:
 (6.20)
(6.20)
Решая поставленную задачу, первоначально принимаем, что  — любые числа, удовлетворяющие выражению (6.19). Пусть
— любые числа, удовлетворяющие выражению (6.19). Пусть  — набор чисел, удовлетворяющих (6.20) и дающих
— набор чисел, удовлетворяющих (6.20) и дающих 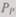 в (6.20) максимальное значение. Так как
в (6.20) максимальное значение. Так как 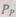 увеличивается с ростом каждого
увеличивается с ростом каждого  должны удовлетворять уравнению
должны удовлетворять уравнению
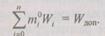 (6.21)
(6.21)
Точка  является точкой условного экстремума функции (6.19) при условии (6.21). На основании теории условного экстремума можно утверждать, что в точке экстремума справедливо следующее равенство:
является точкой условного экстремума функции (6.19) при условии (6.21). На основании теории условного экстремума можно утверждать, что в точке экстремума справедливо следующее равенство:

Подставив в это уравнение значение 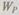 и
и  и, преобразовав его после логарифмирования, определяем
и, преобразовав его после логарифмирования, определяем
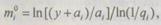
где 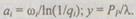 Подставим
Подставим  в (6.21) и будем считать, что единственным корнем уравнения является
в (6.21) и будем считать, что единственным корнем уравнения является 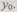 Тогда получим
Тогда получим
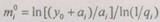 или
или 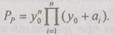
Таким образом, зная вероятность отказа элементов 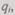 составляющих систему, и их массу W, можно произвести поэлементное резервирование так, что масса резервированной системы не будет превышать допустимого, а вероятность безотказной работы будет максимальной. Аналогично решается и обратная задача.
составляющих систему, и их массу W, можно произвести поэлементное резервирование так, что масса резервированной системы не будет превышать допустимого, а вероятность безотказной работы будет максимальной. Аналогично решается и обратная задача.
Резервирование с восстановлением. Значительный эффект повышения надежности ЭВМ путем резервирования достигается в системах с восстановлением. Основные задачи, рассматриваемые при расчете надежности восстанавливаемых ЭВМ, возникают при следующей ситуации. Исправная ЭВМ начинает эксплуатироваться в момент времени  = 0 и, проработав случайное время
= 0 и, проработав случайное время  выходит из строя. На ремонт требуется случайное время
выходит из строя. На ремонт требуется случайное время 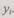
Этот процесс продолжается в течение всего срока службы ЭВМ, причем величины  и
и  (/=1,2,...) независимы. В случайные или заранее установленные моменты времени
(/=1,2,...) независимы. В случайные или заранее установленные моменты времени  (/ = 1,2, ...) могут проводиться профилактические работы случайной или постоянной длительности zt. Процесс усложняется в основном по следующим причинам:
(/ = 1,2, ...) могут проводиться профилактические работы случайной или постоянной длительности zt. Процесс усложняется в основном по следующим причинам:
1) наличие резервных устройств и, как следствие этого, наличие переходов из одного уровня избыточности на другой;
2) дискретность работы устройства с заранее запланированными или случайными моментами начала и окончания работы;
3) ограниченность числа восстановлений (восстановление заключается в простой замене, а запасных устройств конечное число);
4) очередь на обслуживание;
5) ложные восстановления исправных устройств из-за отказа схемы контроля;
6) невозможность начать восстановление устройства или ЭВМ сразу же после его отказа из-за неполноты схемы контроля.
Рассмотрим два наиболее распространенных способа восстановления резервированных систем:
· устранение отказов за время  сразу после их возникновения;
сразу после их возникновения;
· устранение отказов во время профилактики с интервалом 
Определим среднее время  между отказами обобщенной избыточной структуры, если известны закон надежности
между отказами обобщенной избыточной структуры, если известны закон надежности  и функция распределения времени восстановления
и функция распределения времени восстановления 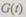 одного устройства. При работе ЭВМ обычно считают, что функции
одного устройства. При работе ЭВМ обычно считают, что функции  и
и 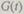 имеют экспоненциальное распределение:
имеют экспоненциальное распределение: 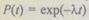 и
и 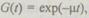 где
где  и
и  — параметры распределений. В этом случае модель надежности избыточной структуры можно свести к однородному марковскому процессу с конечным числом состояний. Пусть
— параметры распределений. В этом случае модель надежности избыточной структуры можно свести к однородному марковскому процессу с конечным числом состояний. Пусть  состоянием избыточной структуры, состоящей из
состоянием избыточной структуры, состоящей из  устройств, будет такое состояние, когда отказало ровно к устройств и
устройств, будет такое состояние, когда отказало ровно к устройств и 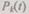 — вероятность этого события.
— вероятность этого события.
Так как при экспоненциальных законах распределения времени безотказной работы и восстановления вероятность изменения состояния ЭВМ на участке  не зависит от момента времени
не зависит от момента времени  то
то
 (6.22)
(6.22)
 (6.23)
(6.23)
Если в избыточной структуре отказало к каналов, то из этого состояния она может перейти в 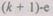 состояние (т. е. откажет еще один из оставшихся
состояние (т. е. откажет еще один из оставшихся  каналов) с вероятностью
каналов) с вероятностью  или с вероятностью
или с вероятностью  перейти в
перейти в  состояние (отремонтируется один из к отказавших каналов). При этом учитывают, что процесс, описываемый исходными уравнениями (6.22) и (6.23), ординарный и вероятностью изменения состояния избыточной структуры за время
состояние (отремонтируется один из к отказавших каналов). При этом учитывают, что процесс, описываемый исходными уравнениями (6.22) и (6.23), ординарный и вероятностью изменения состояния избыточной структуры за время  более одного раза можно пренебречь. Кроме того, полагают, что интенсивность восстановления каждого отказавшего канала не зависит от числа других отказавших каналоа. Составим для этого случая уравнение вероятности
более одного раза можно пренебречь. Кроме того, полагают, что интенсивность восстановления каждого отказавшего канала не зависит от числа других отказавших каналоа. Составим для этого случая уравнение вероятности  состояния резервной структуры в момент времени (t + At), если известны вероятности состояний в момент
состояния резервной структуры в момент времени (t + At), если известны вероятности состояний в момент  По формуле полных вероятностей,
По формуле полных вероятностей,
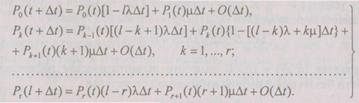 (6.24)
(6.24)
От системы разностных уравнений можно перейти к дифференциальным уравнениям, если члены  перенести в левую часть, правые и левые части разделить на
перенести в левую часть, правые и левые части разделить на 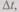 тогда при
тогда при 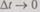 получим
получим
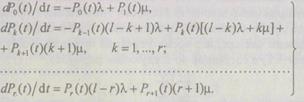 (6.25)
(6.25)
Определим 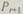 — вероятность отказа избыточной структуры за время / и среднее время безотказной работы резервной группы
— вероятность отказа избыточной структуры за время / и среднее время безотказной работы резервной группы 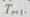 Для решения системы (6.25) относительно
Для решения системы (6.25) относительно  применим преобразование Лапласа:
применим преобразование Лапласа:
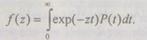 (6.26)
(6.26)
В результате получим систему уравнений относительно функции 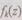 :
:
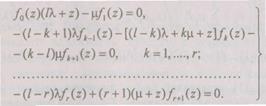 (6.27)
(6.27)
Функцию  найдем по правилу Крамера:где
найдем по правилу Крамера:где 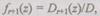 —
— 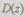 определитель системы (6.27);
определитель системы (6.27); 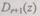 — определитель, полученный исключением столбца коэффициентов при неизвестной
— определитель, полученный исключением столбца коэффициентов при неизвестной 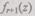 в матрице определителя
в матрице определителя  Искомая вероятность безотказной работы определится
Искомая вероятность безотказной работы определится  по формуле обращения интегрированием по контуру:
по формуле обращения интегрированием по контуру:
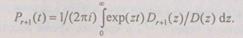 (6.28)
(6.28)
Определение вероятности 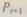 по (6.28) в общем случае связано с громоздкими вычислениями. На практике же представляет интерес случай, когда отказы избыточной структуры являются редкими событиями, т. е. выполняется условие
по (6.28) в общем случае связано с громоздкими вычислениями. На практике же представляет интерес случай, когда отказы избыточной структуры являются редкими событиями, т. е. выполняется условие  Если отношение
Если отношение 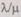 стремится к нулю, то предел отношений определителей Z)r+I(z)/D(z) системы (6.27) равен
стремится к нулю, то предел отношений определителей Z)r+I(z)/D(z) системы (6.27) равен
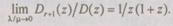 (6.29)
(6.29)
Подставляя (6.29) в (6.28), получим асимптотическое распределение вероятности безотказной работы избыточной структуры:
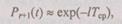 (6.30)
(6.30)
где 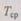 — постоянная величина, имеющая смысл среднего времени безотказной работы избыточной структуры. Формула (6.30) является очень важной в теории избыточных систем с восстановлением, так как все расчеты при экспоненциальном законе надежности значительно упрощаются. При этом среднее время безотказной работы избыточной структуры
— постоянная величина, имеющая смысл среднего времени безотказной работы избыточной структуры. Формула (6.30) является очень важной в теории избыточных систем с восстановлением, так как все расчеты при экспоненциальном законе надежности значительно упрощаются. При этом среднее время безотказной работы избыточной структуры  может быть определено как среднее время перехода процесса (6.24) из нулевого состояния в
может быть определено как среднее время перехода процесса (6.24) из нулевого состояния в 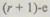 состояние по следующей формуле:
состояние по следующей формуле:
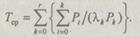 (6.31)
(6.31)
где 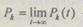 — вероятности, получаемые решением (6.25) путем предельного перехода при
— вероятности, получаемые решением (6.25) путем предельного перехода при  Вероятности
Вероятности 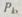 в свою очередь, равны
в свою очередь, равны
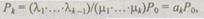 (6.32)
(6.32)
где 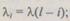 1
1  — вероятность того, что все устройства резервной струк-
— вероятность того, что все устройства резервной струк-
туры исправны, т. е.  Подставляя (6.31) в (6.32), получим
Подставляя (6.31) в (6.32), получим
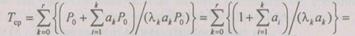
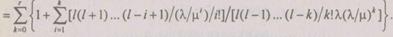 (6.33)
(6.33)
Формула (6.33) определяет точное значение среднего времени безотказной работы избыточной структуры. Ее можно значительно упростить, если воспользоваться допущением, которое было принято при выводе (6.30) для вероятности безотказной работы. В этом случае сумма в числителе выражения (6.33) много меньше единицы и ею можно пренебречь, а общая сумма определяется только слагаемым с малым знаменателем, т. е. при 
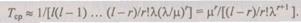 (6.34)
(6.34)
Обозначив в соответствии с (6.22) и (6.33) через  среднее время безотказной работы и через
среднее время безотказной работы и через  среднее время восстановления одного устройства, получим приближенную формулу для определения среднего времени безотказной работы избыточной структуры с восстановлением:
среднее время восстановления одного устройства, получим приближенную формулу для определения среднего времени безотказной работы избыточной структуры с восстановлением:
 (6.35)
(6.35)
В частном случае для систем, когда  получаемт.
получаемт.  т.е. квадратичную зависимость времени
т.е. квадратичную зависимость времени 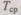 от времени Т.
от времени Т.
Приведем для сравнения среднее время безотказной работы той же избыточной структуры в невосстанавливаемом режиме, когда отказы не устраняются, а накапливаются и при отказе  наступает отказ избыточной структуры:
наступает отказ избыточной структуры:
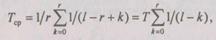 (6.36)
(6.36)
где Т— среднее время безотказной работы одного канала. Из (6.36) видно, что для систем без восстановления среднее время безотказной работы с введением избыточности растет очень медленно. Если сравнить формулу (6.35), определяющую среднее время безотказной работы избыточной структуры с восстановлением, с формулой (6.36) для структуры без восстановления, то значительный выигрыш очевиден.
Пример. Пусть имеется дублированная система. Требуется определить величину Т системы с восстановлением и без восстановления работоспособности при 1=2, г=\,Т= 2000,  При вычислениях будем пользоваться приближенными формулами.
При вычислениях будем пользоваться приближенными формулами.
Для случая резервирования без восстановления из уравнения (6.36) получим Тб.юст = 3000 ч. При резервировании с восстановлением 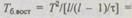 = 2 000 000 ч. Таким образом, эффективность вводимой избыточности при наличии восстановления значительно повышается. И наоборот, избыточность без восстановления для систем длительного пользования малоэффективна и практически очень часто неоправданна.
= 2 000 000 ч. Таким образом, эффективность вводимой избыточности при наличии восстановления значительно повышается. И наоборот, избыточность без восстановления для систем длительного пользования малоэффективна и практически очень часто неоправданна.
Профилактика ЭВМ. Профилактика также принадлежит к способам, позволяющим повысить надежность ЭВМ. Но в отличие от способа, описанного выше, здесь коррекция закона надежности 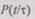 производится не в случайное время, связанное с возникновением отказа и со скачкообразным изменением вида функции
производится не в случайное время, связанное с возникновением отказа и со скачкообразным изменением вида функции 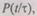 а в заранее запланированные моменты времени. Рассмотрим случай, когда профилактика осуществляется через равные интервалы времени
а в заранее запланированные моменты времени. Рассмотрим случай, когда профилактика осуществляется через равные интервалы времени 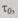 причем время, затрачиваемое на профилактику, мало по сравнению с временем
причем время, затрачиваемое на профилактику, мало по сравнению с временем 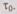 Будем считать также, что во время профилактики происходит полное восстановление свойств надежности ЭВМ. Обозначим вероятность безотказной работы системы в исходном состоянии через
Будем считать также, что во время профилактики происходит полное восстановление свойств надежности ЭВМ. Обозначим вероятность безотказной работы системы в исходном состоянии через 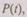 т. е.
т. е. 
Полное восстановление свойств надежности во времени профилактики означает, что для такой системы выполняется равенство
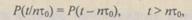 (6.37)
(6.37)
где 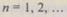 — число профилактик до момента времени
— число профилактик до момента времени  Условие (6.37) показывает влияние профилактики с полным восстановлением на надежность системы.
Условие (6.37) показывает влияние профилактики с полным восстановлением на надежность системы.
Определим надежность систем с профилактикой. Найдем функцию надежности системы 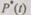 как вероятность того, что система не откажет на интервале времени (0, t), если за это время будет проведено
как вероятность того, что система не откажет на интервале времени (0, t), если за это время будет проведено 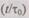 профилактик. Обозначим через
профилактик. Обозначим через  событие, состоящее в том, что система исправно проработает на интервале времени
событие, состоящее в том, что система исправно проработает на интервале времени 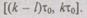 Событие А есть произведение событий Ак, когда система не откажет на интервале времени (0, t) и она не откажет ни на одном из интервалов
Событие А есть произведение событий Ак, когда система не откажет на интервале времени (0, t) и она не откажет ни на одном из интервалов 
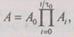 (6.38)
(6.38)
где .  — событие, состоящее в том, что система не откажет на интервале времени
— событие, состоящее в том, что система не откажет на интервале времени 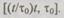 Для вероятности
Для вероятности 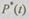 в общем случае
в общем случае
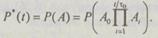
Вероятность произведения событий
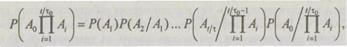
где согласно условию вероятность
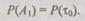
Условные вероятности
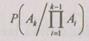
могут быть определены как
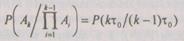 (6.39)
(6.39)
и на основе (6.37) равны
 (6.40)
(6.40)
С учетом (6.41) и (6.42) выражение (6.39) определится как
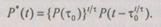 (6.41)
(6.41)
Выражение (6.41) представляет собой искомый закон надежности системы с профилактикой. Через вероятность 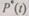 могут быть определены все остальные характеристики системы. Среднее время безотказной работы системы с профилактикой может быть найдено, как
могут быть определены все остальные характеристики системы. Среднее время безотказной работы системы с профилактикой может быть найдено, как
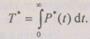 (6.42)
(6.42)
Подставляя значение вероятности 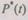 из (6.41) в (6.42), получим
из (6.41) в (6.42), получим
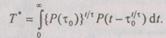
Разобьем интервал интегрирования  функции на
функции на  участки
участки  Тогда
Тогда
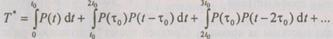
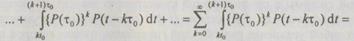
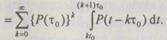 (6.43)
(6.43)
В (6.43) применим подстановку вида 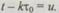 Тогда
Тогда
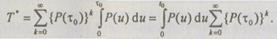 (6.44)
(6.44)
Сумма в (6.44) представляет собой геометрическую прогрессию с первым членом, равным единице, и знаменателем 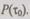 Свертывая сумму, получим
Свертывая сумму, получим
 (6.45)
(6.45)
Выражение (6.45) представляет собой среднее время безотказной работы системы с профилактикой, определяемое через исходный закон надежности 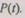 Нахождение точного времени по (6.45) предполагает вычисление определенного интеграла. Можно получить практически более удобную формулу, если принять, что вероятность безотказной работы системы за время профилактики
Нахождение точного времени по (6.45) предполагает вычисление определенного интеграла. Можно получить практически более удобную формулу, если принять, что вероятность безотказной работы системы за время профилактики 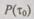 близка к единице. Так как на интервале профилактики вероятность безотказной работы удовлетворяет соотношению
близка к единице. Так как на интервале профилактики вероятность безотказной работы удовлетворяет соотношению 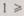
 то получим неравенство
то получим неравенство
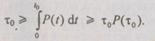
Если вероятность 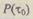 близка к единице, то значение интеграла
близка к единице, то значение интеграла  практически равно интервалу времени профилактики
практически равно интервалу времени профилактики 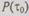 и тогда для среднего времени безотказной работы системы с профилактикой
и тогда для среднего времени безотказной работы системы с профилактикой
 (6.46)
(6.46)

При этом относительная ошибка не превосходит значения вероятности 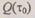 отказа системы за время
отказа системы за время  Среднее время безотказной работы
Среднее время безотказной работы 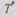 избыточной системы с профилактикой существенно зависит от интервала
избыточной системы с профилактикой существенно зависит от интервала 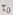 времени профилактики. Выражение (6.46) относительно аргумента представляет собой уравнение равнобочной гиперболы, график которой показан на рис. 6.10. Из рисунка видно, что эффективность профилактики различна на различных участках интервала
времени профилактики. Выражение (6.46) относительно аргумента представляет собой уравнение равнобочной гиперболы, график которой показан на рис. 6.10. Из рисунка видно, что эффективность профилактики различна на различных участках интервала 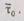 Так, при
Так, при  влияние профилактики на надежность системы слабое, а при
влияние профилактики на надежность системы слабое, а при  — очень сильное. Следовательно,
— очень сильное. Следовательно,  интервал времени профилактики следует выбирать из соотношения
интервал времени профилактики следует выбирать из соотношения
Восстановление во время профилактики упрощает эксплуатацию избыточных систем, так как сразу после возникновения корректируемого отказа требуются сложные и громоздкие системы аппаратурного контроля и специальные конструкции систем, позволяющие без нарушения функционирования выводить в ремонт отказавшее оборудование. В связи с этим восстановление в момент возникновения отказа возможно лишь при высоких уровнях введения избыточности.
Дата добавления: 2015-10-29; просмотров: 2834;
