Информационные методы повышения надежности ЭВМ

Один из наиболее удобных и гибких методов повышения надежности ЭВМ — применение корректирующих кодов. В некоторых условиях, например при кратковременных сеансах работы, когда ресурсы надежности почти не расходуются, коррекция сбоев, вызванных различного рода помехами, имеет решающее значение для обеспечения нормального функционирования систем. Достоинства корректирующих кодов следующие:

а) исправление ошибок без перерывов в работе;

б) способ кодирования и применяемый код выбирают в зависимости от алгоритма функционирования данного цифрового устройства, что дает возможность согласования корректирующей способности кода со статическими характеристиками потока ошибок устройства и уменьшения избыточности, требуемой для коррекции ошибок;

в) использование корректирующих кодов позволяет учесть необходимость устранения влияния ошибок в устройстве, последовательно на всех этапах проектирования, начиная с алгоритма функционирования.

Избыточность может быть либо временной, либо пространственной. Временная избыточность связана с увеличением времени решения задачи (в частном случае задача может быть решена, например, дважды) и вводится программным путем, являясь основой программного способа обнаружения и исправления ошибок. Пространственная избыточность заключается в удлинении кодов чисел, в которые вводят дополнительные (контрольные) разряды.

Идея обнаружения и исправления ошибок с использованием избыточности состоит в следующем. Все множество 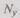выходных слов устройства разбивают на подмножество 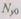разрешенных кодовых слов, т. е. таких слов, которые могут появиться в результате правильного выполнения логических и арифметических операций, и подмножество запрещенных кодовых слов, т. е. таких слов, которые могут появиться только в результате ошибки. 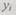Появившееся на выходе устройства слово подвергают анализу: если слово относится к подмножеству разрешенных слов, то оно считается правильным результатом и декодирующее устройство переводит его в соответствующее выходное слово 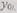если же слово оказывается элементом подмножества запрещенных слов, то это свидетельствует о наличии ошибки. Для исправления обнаруженных ошибок запрещенные кодовые слова разбиваются на группы: каждому разрешенному кодовому слову соответствует одна такая группа.

При декодировании обнаруженное на выходе устройства запрещенное кодовое слово заменяется разрешенным словом, в группу которого оно входит. Тем самым ошибка исправляется. При этом работа декодирующего устройства усложняется. Процесс построения корректирующего кода состоит из следующих этапов:

Этап 1 — выявление наиболее вероятных ошибок для заданного способа функционирования устройства или наиболее опасных в условиях его использования.

Этап 2 — формирование избыточного множества выходных слов, разделение этого множества на подмножества разрешенных и запрещенных кодовых слов и образование декодировочных групп.

Этап 3 — разработка рационального способа декодирования выходных слов, позволяющего реализовать относительно несложными техническими средствами обнаружение и исправление обусловленных ошибок.

Этап 4 — организация множества входных слов так, чтобы заданное преобразование, выполненное над любым словом этого множества, дало на выходе автомата слово, принадлежащее к подмножеству разрешенных кодовых слов.

При построении ЭВМ, предназначенной для решения определенного класса задач, важным вопросом является рациональный выбор уровня, на котором следует применять корректирующий код. Вычислительная машина состоит из отдельных устройств: запоминающего, арифметического, внешнего и т. п. В каждом устройстве информация претерпевает определенные изменения. Эти устройства состоят из отдельных блоков — сумматоров, регистров и т. п., которые набраны из простейших логических элементов (триггеров, схем И, ИЛИ, НЕ и т. п.). Корректирующие коды применяют на любом из этих уровней структуры машины. Однако результаты при этом получают различные. Может оказаться, например, что корректировать ошибки в работе отдельных логических схем значительно труднее, чем в работе сумматора в целом. Далее, если контроль правильности и исправления ошибок в работе отдельных блоков и устройств машины осуществить сложно, то в некоторых случаях прохождение всей задачи легко контролируется применением простейших принципов, например путем повторного счета.

Коды с повторениями. Среди корректирующих кодов особое место занимают коды с повторениями. Использование этих кодов дает возможность обнаруживать и исправлять ошибки. Их можно применять во всех без исключения случаях. При этом алгоритм функционирования устройства может быть задан любым способом и используется для реализации произволь­ного преобразования информации. Применяя код с повторениями необхо­димая избыточность создается многократным повторением одного и того же слова на входе. При правильной работе устройства слово на его выходе представляет собой кратное повторение слова являющегося результатом правильного преобразования слова При отсутствии ошибок любая из к частей слова может быть взята в качестве результата. Задача декодирующего устройства в этом случае сводится к выведению одной части слова у,.

При наличии случайных ошибок некоторые из к частных результатов, входящих в слово 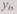отличаются от слова Сравнивая между собой к частей слова у,, можно выявить ошибки, если число одинаковых ошибок меньше к. Сравнение к частных результатов и выработку сигнала ошибки (при несовпадении их) выполняет декодирующее устройство. Если вероятность ошибки в одном частном преобразовании невелика и есть основания предполагать, что большая часть из к частных результатов верна, то ошибки мо­гут быть исправлены. Для этого достаточно принять в качестве правильного результата то частное решение, которое встречается в словах 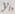большее количество раз. Если определить полезный эффект от применения кода с повторениями при получении неверных частных результатов в слове 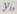при котором ошибка обнаруживается или исправляется, то можно убедиться в справедливости следующих соотношений:

для обнаружения всех ошибок кратности необходимо, чтобы повторений было

для исправления всех ошибок кратности необходимо число повторений

Зададимся вопросом. Какой выигрыш в надежности дает применение кодов с повторениями? Общего ответа на этот вопрос дать нельзя. Лишь для одного частного случая вероятностных свойств автомата можно сделать заключение об эффективности применения кодов с повторениями. Пусть вероятностные свойства автомата описываются таким образом:

вероятность получения правильного результата равна Р независимо от конкретного значения входного слова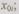

при подаче на вход автомата входного слова на его выходе с равной вероятностью может быть получено любое ошибочное выходное слово, соответственно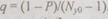

Применим А-кратное ( - нечетное) повторение слов , на входе устройства. Декодирование слов получаемых на выходе, будем выполнять по принципу большинства, полагая правильным тот частный результат который в слове появился большее число раз. Количество правильных частных результатов в к повторениях обозначим S. При декодировании по большинству правильный результат преобразования на выходе схемы (т. е. после декодирующего устройства) получается, если:

1) (при этом любой неверный частный результат может появиться не более раз, так что при декодировании не может быть выдан ложный результат);

2) (при этом ни один из возможных неверных результатов в остальных к - S повторениях не появился S - 1 раз).

Вероятность появления правильного частного результата точно S раз в к повторениях будет

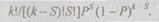
Вероятность появления правильного частного результата не менее раз равна

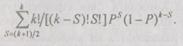
Вероятность появления в оставшихся к - S повторениях какого-либо одного вероятного частного результата точно t раз равна

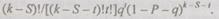
Вероятность появления в оставшихся повторениях какого-либо одного неверного частного результата не более 5- 1 раз будет

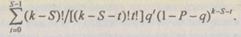
Вероятность того, что ни один из возможных неверных решений не появится в к - S повторениях более S - 1 раз, равна

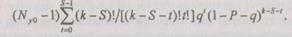
Таким образом, для вероятности 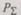получения правильного результата после декодирования можно записать:

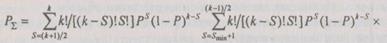
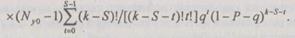
Анализ этого выражения показывает, что при вероятность 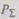монотонно возрастает с ростом числа повторений к и при Это

означает, что, выбирая достаточно большое значение к, можно получить сколь угодно высокую надежность преобразования информации. Кроме положительных свойств коды с повторениями имеют два существенных недостатка:

1) повышение надежности достигается введением относительно очень большой информационной избыточности;

2) коды с повторениями корректируют только случайные ошибки (сбои) в работе устройства.

Если устройство дает систематическую ошибку (отказ) при преобразовании входного слова то никаким количеством повторений эта ошибка не может быть обнаружена или тем более исправлена. Во многих случаях можно построить корректирующие коды, обеспечивающие тот же эффект коррекции при значительно меньшей избыточности, чем коды с повторе­ниями. Это относится к классу преобразований, но в этих случаях выигрыш в избыточности получается очень существенным.

Коды Хэмминга. Более просто выполняются процессы кодирования и декодирования в кодах Хэмминга. Они характеризуются следующими основными чертами: все кодовые слова имеют равную длину; все символы кодового слова четко разделяются на информационные (переносящие информацию и совпадающие с символами не избыточного слова) и проверочные (предназначенные для целей контроля и исправления); те и другие символы занимают вполне определенные фиксированные позиции кодовых слов. Выбор проверочных символов (процесс кодирования), а также обнаружение и исправление ошибок (процесс декодирования) осуществляются с помощью проверок на четность, т. е. подсчетом по модулю 2.

В ЭВМ параллельного действия более вероятны одиночные ошибки, обнаружение и исправление которых обычно осуществляют с помощью кодов Хэмминга. Код с обнаружением однократной ошибки можно получить, прибавив к неизбыточному кодовому слову один проверочный разряд. Символ (0 или 1) в этом разряде выбирают из условия четности числа единиц в полном (избыточном) кодовом слове. Это означает, что сумма всех символов кодового слова по модулю 2 должна быть равна нулю. Если позиции кодового слова пронумеровать по порядку справа налево, а символы, стоящие в этих позициях, обозначить то сформулированное выше условие можно записать так:

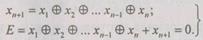(6.47)

В этом случае подмножества разрешенных и запрещенных кодовых слов делят полное множество слов на две равные части. Переход между ними осуществляют изменением значения одного символа. Поэтому эти множества можно поменять местами, т. е. формировать разрешенные кодовые слова по принципу нечетности количества единиц в слове.

Если в процессе преобразования информации возникает любая однократная ошибка (в информационных или проверочных символах), то условие (6.47) нарушается и ошибка обнаруживается при проверке. Обнаруживаются ошибки и более высокой кратности, если кратность эта нечетна. Размещение проверочного символа в кодовом слове роли не играет. Обычно его ставят в конце слова после всех информационных символов. Для построения кода, исправляющего одиночные ошибки, необходимо организовать проверки на четность так, чтобы непосредственно получить число, указывающее номер позиции искаженного символа. Достигается это тем, что контрольные суммы Е по модулю 2, получаемые в результате проверок ("являющиеся двоичными символами), записывают одну за другой: 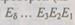и рассматривают как 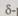разрядное двоичное число, обозначающее номер искаженной позиции. Это число называют контрольным.

Пусть не избыточное кодовое слово состоит из 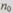(информационных) символов. Для построения кода с коррекцией к ним добавляют к проверочных символов, тогда кодовое слово в корректирующем коде имеет 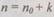позиций. Разрядность контрольного числа, указывающего номер позиции искаженного символа, должна быть достаточной, чтобы отобразить число, равное п. Поэтому необходимое количество проверок 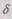определяется нера­венством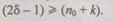

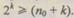
Число проверок на четность не может быть больше числа проверочных символов к, поскольку в противном случае эти проверки не будут независимыми; следовательно, Итак, количество необходимых добавочных символов кодового слова к и одновременно количество необходимых проверок на четность можно найти из неравенства или

Определим позиции кодового слова, символы которых должны принимать участие в каждой из к проверок. Если кодовое слово не содержит ошибок, то контрольное двоичное число должно изображать нуль. Если в младшем разряде контрольного числа стоит единица, то это означает ошибку в одной из тех позиций слов, номера которых в двоичной системе счисления имеют единицу в младшем разряде. А это все нечетные номера. Следовательно, первая проверка должна охватывать все символы, стоящие на нечетных позициях:

(6.48)

Единица во втором разряде контрольного числа означает ошибку в одной из тех позиций, двоичные номера которых (2, 3, 6, 7, 10, 11, 14, 15 и т. д.) имеют единицу во втором разряде. Рассуждая подобным образом, можно записать для второй, третьей, четвертой и проверок, начинающихся с символа, стоящего в 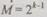позиции,

(6.49) (6.50) (6.51)

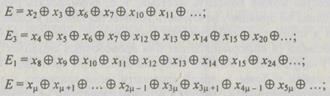(6.52)

Далее остается выбрать в кодовом слове длиной 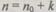символов позиции, отводимые для информационных и проверочных символов. Для проверочных символов позиции следует выбирать так, чтобы кодирование выполнялось, возможно, более просто. Выделим в формулах (6.48)—(6.52) позиции, встречающиеся только в одной проверке: 1, 2, 4, 6, 8, 16, ..., т. е. позиции с номерами, являющимися целыми степенями двойки. Если разместить проверочные символы в этих позициях, то, приняв выражения (6.48)—(6.52) равными нулю, получим соотношения, реализуемые в процессе кодирования:

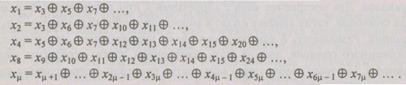
Для практической реализации кодов Хэмминга необходимо разработать кодирующее устройство, определяющее значения проверочных символов и размещающее их в соответствующих позициях кодового слова, и декодирующее устройство, подсчитывающее контрольные суммы, выявляющее наличие ошибки, определяющее номер позиции искаженного символа, автоматически исправляющее ошибку и выделяющее информационные символы кодового слова. Построение кодирующего и декодирующего устройств существенно облегчается тем, что суммирование ведется по модулю 2, номер позиции искаженного символа получается непосредственно в двоичном коде и исправление ошибки в этой позиции сводится к замене символа на обратный. Рассмотренные выше коды целесообразно применять в логических устройствах и устройствах управления.

Арифметические коды. Для коррекции ошибок в устройствах, выполняющих математические операции вычитания, сложения и умножения, наиболее эффективными являются арифметические коды, которые можно подразделить на коды:

а) обнаруживающие ошибки;

б) исправляющие ошибки.

Идея построения арифметических кодов состоит в том, что в их контрольных разрядах записывают остаток от деления исходного кодируемого числа на некоторое заранее заданное целое число А. При этом все машинные числа можно условно рассматривать как целые. Эти коды обнаружат все ошибки, за исключением тех, которые кратны выбранному модулю. Арифметичность кодов основана на том, что остаток от деления на А суммы (произведения) должен быть равен сумме (произведению) остатков от деления на А исходных чисел, т. е. в этом случае есть прямая связь между контрольными разрядами операндов и результатом операции. Существует три способа кодирования чисел в арифметических кодах.

Первый способ заключается в нахождении остатка /?# от деления заданного числа N на выбранный модуль А. Например, N = 1010, А = 3, R(N) = 01, код 101001. Этот способ кодирования используют, когда контрольные и информационные разряды обрабатываются отдельно. Второй способ состоит в выполнении следующих последовательных операций:

задать число контрольных разрядов С;

умножить заданное число N на ;

вычислить I

сложить 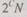с числом (в полученном результате С младших разрядов являются контрольными). Например, N= 1010, Л = 3, С = 01, код 101010. Этот способ применяют, когда сами числа должны обладать свойствами самоконтролируемости.

Максимальное значение N для кодов, полученных первым и вторым способами, определяется формулой 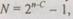где п — число разрядов в кодовом слове, включая контрольные.

Третий способ заключается в умножении заданного числа N на модуль А. Это более эффективный способ кодирования слов, в нем

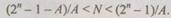
В отличие от способов 1 и 2 кодирования способ 3 не имеет отдельно расположенных информационных и контрольных разрядов. При этом способе кодирования получение информационных разрядов возможно лишь после деления кодового слова на модуль А. Необходимо отметить, что при построении арифметических устройств, использующих способ 3 кодирования, избегают постоянного умножения и деления чисел на модуль А по мере прохождения их через сумматор. Только при выводе данных из арифметических устройств производят деление результатов на модуль А для получения информационных символов. Для организации контроля арифметических операций (сложения или умножения) в машинах помимо обычного арифметического устройства для операндов необходимо иметь дополнительное оборудование:

а) сумматоры (умножители) для остатков операндов;

б) схему быстрого определения остатка от деления суммы (произведения) на модуль А,

в) схему сравнения суммы (произведения) остатков операндов с остатком их суммы (произведения).

Для характеристики ошибок, возникающих в арифметических операциях, удобно ввести понятие числового значения ошибки 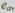равного числу, на которое изменяется правильный результат при возникновении данной ошибки. Параметр 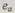может быть положительным и отрицательным и зависит от вектора ошибки е, который использовался для описания ошибок при передаче или логических преобразованиях информации.

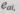Выбор параметра А в соответствии с числовым значением тех ошибок, которые должны быть обнаружены, определяется выражением (6.53) для всех из перечня обнаруживаемых ошибок.

Выражению (6.53) могут соответствовать несколько значений параметра А. Поэтому на практике целесообразно выбрать наименьший из них. Определение минимального значения параметра А обычно достигается простым перебором всех целых чисел. Наибольшее практическое значение имеет обнаружение однократных ошибок, не связанное с введением большой избыточности. Экономичность преобразователя с обнаружением однократных ошибок тем выше, чем больше разрядность участвующих в операции двоичных чисел. Анализ (6.53) показывает, что при обнаружении всех однократных ошибок в арифметических операциях сложения, вычитания и умножения оптимальное значение параметра А равно трем, т. е. достаточно двух проверочных двоичных символов независимо от разрядности участвующих в операции чисел.

Коды Брауна. При реализации способа обнаружения однократных ошибок большие трудности возникают при создании устройств, определяющих остатки по модулю 3: деление двоичных чисел на 3 приводит к существенному недостатку — правильность выполнения операций сложения, вычитания или умножения контролируется с помощью значительно более сложной операции деления. Устранить этот недостаток можно использованием кодов Брауна, с помощью которых обосновывается легко реализуемый аппаратно способ определения остатков от деления чисел, представленных в двоичной системе счисления, на 3.

Идея кодов Брауна основана на положении, что остаток от деления на 3 целого числа представленного в двоичной системе счисления кодовым словом д:, равен разности числа единиц в нечетных позициях числа х, и числа единиц в четных позициях:

где — вес кодового слова, составленного из нечетных символов х; — вес кодового слова, образованного четными символами.

Схема контроля по модулю 3 для 4-разрядного кодового слова приведена на рис. 6.11.

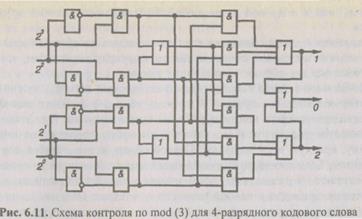
Определить значения при обнаружении двойных ошибок можно следующим образом:

При выборе значения модуля А необходимо также учитывать стоимость схем контроля; увеличение длины чисел; увеличение времени, необходимого для выполнения арифметических операций. Если при выполнении арифметических операций произошла ошибка, то для ее исправления необходимо выполнение двух условий:

1) для всех из перечня ошибок, подлежащих исправлению;

2) для любой пары неравных ошибок из общего перечня.

Параметр А для исправления всех однократных ошибок выбирают точно так же, как и в случае обнаружения всех двукратных ошибок, в частности приемлемы все данные, приведенные выше.

Чтобы можно было исправить арифметическую ошибку, нужно иметь корректирующий код с проверкой по модулю Этого можно достичь, если производить контроль по нескольким модулям. При этом не об­наруживаются только ошибки, которые изменяют проверяемое число на величину, кратную всем модулям. Способ обнаружения ошибок состоит в следующем. Если ожидаемый и найденный сверткой остатки не совпадают, то определяют их разность со своим знаком и находят те разряды, искажение которых приводит к данной разности в остатках. Обычно таких разрядов по одному модулю получают несколько. Затем такую же процедуру производят и с остатками по второму модулю. Далее все «подозрительные» разряды анализируют. Если найдут разряд, «подозрительный» по первому и второму модулю, то, очевидно, он и является ошибочным. Исправление производят сложением по модулю 2 содержимого ошибочного разряда с единицей.

Равновесные коды. При передаче данных внутри устройств ЭВМ, а также по каналам связи, в которых наблюдаются асимметричные ошибки, большое распространение получили равновесные коды (при асимметричных ошибках имеют место только переходы либо ). В равновесном

коде используют слова, имеющие некоторое фиксированное число единиц т в и-разрядном слове, поэтому они обнаруживают асимметричные ошибки любой кратности. Существует большое количество равновесных кодов т из п, в которых общее число разрешенных кодовых слов N определяется как 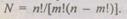Наибольшее распространение получили равновесные

коды «2 из 5», «4 из 8», «2 из 7». Рассмотрим применение кода «2 из 5» для контроля работы различных устройств ЭВМ:

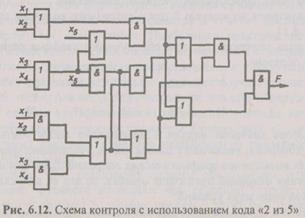
Анализ данных показывает, что все двоичные слова равновесного кода содержат две 1 и три 0. Следовательно, работа схемы контроля может быть описана с помощью функций алгебры логики: 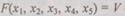(3, 5, 6, 9,10, 12, 17, 18,20,24). На рис. 6.12 показана схема контроля для кода «2 из 5», построенная с использованием схем И и ИЛИ на два входа. Недостаток рав­новесных кодов в том, что они не обнаруживают ошибки, приводящие к одинаковому количеству переходов 0 -> 1 и 1 -> 0. Но на практике вероятность появления таких ошибок чрезвычайно мала.

Введение структурной и информационной избыточности для повышения надежности ЭВМ будет иметь низкую эффективность, если при проек­тировании вычислительных машин нерационально решены вопросы конст­руирования различных узлов. Так, при резервировании ограничения в габа­ритных размерах и весе могут привести к схемам (или другим функциональным устройствам), в которых используются малогабаритные, менее надежные элементы, размещаемые в располагаемом объеме. При этих условиях надежность резервированной системы может оказаться меньше, чем надежность нерезервированной системы. Кроме того, вибрация или изменения температуры могут вызвать отказ резервированных систем. При этих условиях необходимо направить усилия конструктора на защиту от перегрева, ослабление вибраций и ударов или на другую защиту схемы или системы от воздействия окружающих условий.

Конструктор, стремящийся обеспечить высокую надежность ЭВМ, должен помнить, что чем проще конструкция, тем выше надежность; стан­дартизация элементов также повышает надежность ЭВМ, поскольку стан­дартные элементы и схемы обычно проходят тщательную приработку и ве­роятность появления каких-либо неприятных неожиданностей при их ис­пользовании очень мала. Конструктор должен также проявлять интерес к факторам инженерной психологии. Следует заботиться о том, чтобы непра­вильная сборка или неправильное использование созданной конструкции были практически невозможны. Длина кабелей должна выбираться такой, чтобы можно было соединить соответствующим разъемом необходимый кабель; разъемы должны отличаться по размерам, чтобы подходил разъем только соответствующего кабеля. Если поставлено условие замены функционального узла, то проблемы, связанные с удалением и заменой его малоквалифицированным персоналом в эксплуатационных условиях, должны быть решены оптимальным образом.

Важное значение для повышения надежности ЭВМ имеют обеспечиваемые конструкцией возможности проведения профилактики и контроля. Разработчик функциональной схемы по возможности должен так выбирать принцип действия и схему устройства и его узлов, чтобы они могли быть подвергнуты полной неразрушающей функциональной проверке.

Один из методов повышения надежности ЭВМ — это создание облегченных условий эксплуатации. Этого можно добиться путём обеспечения термостатирования или температурного контроля, ослабления ударных нагрузок с помощью амортизации, уменьшения влажности при транспортировке, хранении и эксплуатации, применения в замкнутом объеме влагопоглотителей и т. п. Несмотря на то, что изменение окружающих условий (обычно путем применения специальных контейнеров, в которых поддерживаются требуемые условия) обходится очень дорого и связано с дополнительными трудностями, тем не менее оно представляет собой выход из положения в тех случаях, когда невозможно найти приемлемое конструктивное решение для обеспечения надежности при работе во всем диапазоне предельных условий.

Другой метод конструирования, направленный на повышение надежности, заключается в преднамеренном решении конструктора не рассчитывать конструкцию на самые худшие рабочие условия. Приняв такое решение, конструктор имеет возможность использовать менее сложную конструкцию, обладающую более высокой надежностью при всех, кроме наихудших сочетаний, условиях. Вероятность столкнуться с худшими сочетаниями окружающих условий при этом статистически весьма мала.

Эффективный метод повышения надежности — проявление внимания ко всем случаям отказов и неувязкам в конструкции, сведения о которых поступают из отчетов о разработке, конструктивного анализа, формальных программ испытаний, отчетов о неисправностях и отказах при эксплуатации и материалов исследований причин отказов. Оперативные корректировочные меры могут в значительной степени повысить надежность.