Собственные частоты контактной подвески и резонансные скорости
Контактная подвеска является колебательной системой со многими степенями свободы и характеризуется спектром собственных частот.
По данным отечественных исследований (В.А. Вологин, ВНИИЖТ) основная частота собственных колебаний с достаточной точностью определяется выражением
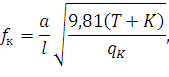
| (190) |
где a – коэффициент, зависящий от конструктивного исполнения опорного узла подвески и принимаемый равным 0,435 при рессорных и 0,5 при простых опорных струнах;
qк – распределенная линейная нагрузка для КП, Н/м;
l – длина пролета, м.
На основании частотных характеристик подвески определяют так называемую резонансную (или критическую) скорость, которая имеет место при равенстве частот собственных и вынужденных колебаний контактной подвески и определяется формулой (в км/ч)
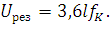
| (191) |
Для скоростных подвесок эта скорость обычно лежит ниже конструктивной скорости. Желательно, чтобы резонансная скорость не совпадала с теми скоростями, при которых планируется эксплуатация контактной подвески.
5.2.7. Значения статических и динамических характеристик для скоростных контактных подвесок
Для скоростных контактных подвесок зарубежными
экспериментальными исследованиями (а также математи- ческим моделированием) при различных скоростях движе- ния установлены допускаемые значения для статических и динамических характеристик контактной подвески. Если характеристики подвески «укладываются» в эти значения для заданной скорости, то с большой вероятностью мож- но говорить о том, что контактная подвеска годится для движения при этой скорости с приемлемым качеством то- косъема. Окончательные выводы делаются на основании математического моделирования или натурных испытаний.
Требования к статическим и динамическим характеристикам приведены в международных нормативных документах. Приведем, некоторые из них для скоростных подвесок переменного тока, согласно UIC 799 и TSI Energy.
Таблица 10 – Требования к статическим и динамическим характеристикам контактной подвески согласно UIC 799 и TSI Energy
| Параметры | 200<V≤230 км/ч | 230<V≤300 км/ч | V>300 км/ч |
| Максимальная эластичность (в середине пролета), мм/даН | |||
| Относительная неравномерность эластичности, ℅ | <20 (<40) | <10 (<40) | <10(<25) |
| Скорость распространения волны, км/ч | >396 | >432 | >Vmax+144 |
| Коэффициент Доплера | >0,26 | >0,18 | >0,17 |
| Коэффициент отражения | <0,5 | <0,4 | <0,4 |
| Коэффициент усиления | <1,9 | <2,2 | <2,3 |
Примечание: 1 – в скобках приведены значения для подвесок без рессорного троса; 2 – параметры эластичности определяются при контактном нажатии 100 Н
6. Ветроустойчивость контактных подвесок
6.1. Основные положения
Надежная работа системы «контактная подвеска – токоприемник» в условиях ветровых воздействий на нее обеспечивается в том случае, если наибольшее отклонение контактного провода по горизонтали от оси токоприемника не превышает максимально допустимого bкдоп, установленного нормативными документами:
bкдоп = 0, 5 м на прямых;
bкдоп = 0, 45 м на кривых.
Длина пролета, при которой под действием ветровой нагрузки КП отклоняется на максимально допустимую величину bкдоп является максимально допускаемой по условию обеспечения необходимой ветроустойчивости подвески (lmax).
Наибольшее отклонение контактный провод может иметь в одном из двух режимов: в РВmaxили в РГВ. Поэтому lmax определяется для двух этих режимов. Режим в котором lmax имеет наименьшее значение является наиболее тяжелым и эта наименьшая длина пролета и принимается в качестве максимально допускаемой по ветроустойчивости (если она не должна быть снижена по другим критериям).
В общем случае имеется три критерия, по которым ограничивают длину пролета:
1. Ограничение по условию обеспечения необходимой ветроустойчивости.
2. Ограничение по условию обеспечения надежного токосъема. Для скоростей движения до 160 км/ч lmax по этому условию принимается 70 м (для скоростных подвесок – меньше, например в КС-200 lmax = 65 м).
3. Ограничение по условию соблюдения вертикальных габаритов КП от УГР. Для компенсированных подвесок lmax определяется с учетом понижения контактного провода при гололеде, для полукомпенсированных – с учетом изменения положения КП при изменении температуры и при гололеде.
lmax рассчитывают по этим трем критериям, сравнивают полученные значения и окончательно принимают равной меньшей из трех.
Т.к. от длины пролетов зависит в значительной степени стоимость сооружения контактной сети, то при проектировании стараются сделать длины пролетов по-возможности большими, но не более окончательно принятой lmax
6.2. Определение lmax по условию обеспечения ветроустойчивости для обычных одинарных контактных подвесок
Определение ветровых отклонений проводов, максимально допускаемых длин пролетов может осуществляться по двум методикам:
– динамической, учитывающей динамические процессы, возникающие при действии на провода фактически неравномерной ветровой нагрузки;
– статической, основанной на учете статической равномерной ветровой нагрузки на провода с учетом коэффициентов, характеризующих конкретные условия трассы с точки зрения защищенности от ветра.
Более совершенной является динамическая методика. Но мы для понимания смысла расчетов, начнем с рассмотрения статической методики, причем упрощенной.
На рисунке 107 рассмотрен контактный провод в пролете контактной подвески на прямом участке пути, на который действует равномерно распределенная ветровая нагрузка pк. Пусть на первой опоре зигзаг контактного провода направлен от опоры и по величине равен a, а на второй опоре зигзаг направлен к опоре и по величине также равен a.
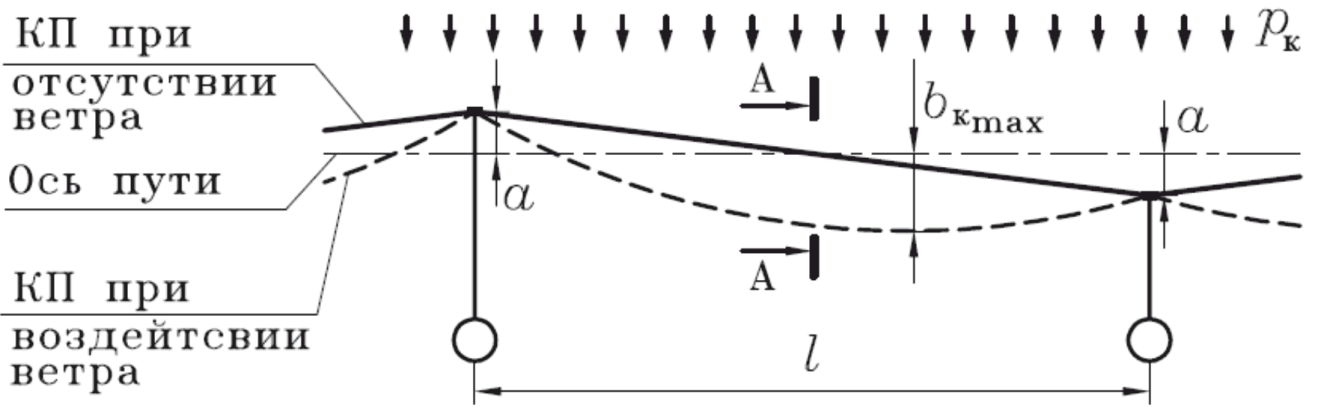
Рисунок 107 – Выдувание КП
Найдем максимальное ветровое отклонение провода в пролете относительно оси пути bкmax. Для расчета мы можем воспользоваться формулой для свободно подвешенного провода формула. Соответствующая расчетная схема приведена на рисунке 108.
Наша ситуация полностью эквивалентна рассмотрению свободно подвешенного провода с равномерно распределенной нагрузкой от веса при точках подвеса, расположенных на разных уровнях, которое мы проводили в разделе 3.1.7 на стр. 16. Вся разница в том, что данном случае мы рассматриваем не вертикальную, а горизонтальную плоскость, а вместо равномерно распределенной нагрузки от веса у нас равномерно распределенная нагрузка от ветра. В разделе 3.1.7 на стр. 16 мы выводили уравнение для стрелы провеса провода относительно верхней точки подвеса (формула (3.54) на стр. 16):

Рисунок 108 – Расчетная схема для нахождения bкmax
Подставим значения: H=K, h=2a, g = pк. С учетом того, что bкmax=fA−a, формула примет вид
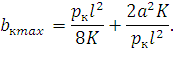
| (192) |
Наибольшее допустимое значение длины пролета будет в том случае, когда наибольшее отклонение провода bкmax получится равным наибольшему допустимому отклонению провода от оси токоприемника bкдоп. Поэтому, приняв в уравнении (6.2) bкmax = bкдоп необходимо решить его относительно l, и получить выражение для максимально допускаемой длины пролета lmax.
Уравнение является биквадратным (т.е. квадратным относительно l2), решение его не представляет трудностей. Опуская выкладки, запишем результат
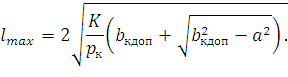
| (193) |
Заметим, что максимально допускаемая длина пролета увеличивается с увеличением натяжения КП, допустимого отклонения bкдоп, и уменьшается с увеличением ветровой нагрузки и зигзага.
Наше рассмотрение было упрощенным: мы не учитывали прогиб опоры при воздействии ветра и влияние несущего троса на отклонение контактного провода. Учтем эти факторы при рассмотрении более совершенной динамической методики, которая дополнительно учитывает динамические процессы при воздействии ветра.
Выражение (193) перепишется:
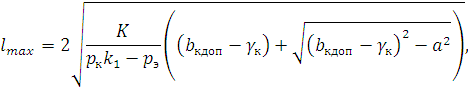
| (194) |
где k1 – коэффициент, учитывающий динамические процессы при воздействии ветровой нагрузки;
pэ – эквивалентная нагрузка, характеризующая влияние НТ на отклонение КП, Н/м;
γk – прогиб опоры на уровне КП под действием ветровой нагрузки, м.
Коэффициент k1 находится по формуле
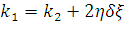
| (195) |
где k2 – коэффициент, учитывающий упругие деформации провода при его отклонении;
η – коэффициент, учитывающий пульсацию ветра и зависящий от длины пролета lmax;
δ – коэффициент, учитывающий пульсацию ветра и зависящий от скорости ветра
ξ – коэффициент динамичности, зависящий от веса КП с учетом гололеда.
Коэффициенты являются справочными данными [2].
Коэффициент k2 определяется по формуле:
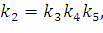
| (196) |
где k3 – коэффициент, определяемый в зависимости от длины пролета lmax;
k4 – коэффициент, зависящий от скорости ветра;
k5 – коэффициент, зависящий от веса КП с учетом гололеда.
Эквивалентная нагрузка pэ определяется по формуле

| (197) |
где T – натяжение НТ, Н;
pн – нормативная ветровая нагрузка на НТ, Н/м;
hи – длина гирлянды изоляторов, м;
qн – результирующая нагрузка на НТ, Н/м;
γк – изменение прогиба опоры на уровне НТ под действием ветровой нагрузки, м;
eср – средняя длина струн в средней части пролета lmax, м;
gк – нагрузка от веса одного КП (в режиме гололеда – вместе с гололедом), Н/м;
nк – число контактных проводов;
Значения величин в приведенных формулах должны соответствовать режиму, для которого определяется lmax.
Средняя длина струн в средней части пролета lmax определяется по формуле:
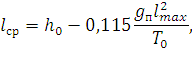
| (198) |
где h0 – конструктивная высота подвески, м;
gп – нагрузка от веса всех проводов подвески на НТ (в данном случае при отсутствии гололеда и ветра), Н/м.
Для пролетов длиной более 70 м значение eср принимается таким же, как и для пролетов длиной 70 м.
Влияние отклонения несущего троса на отклонение контактного провода и значение параметров, входящих в выражение для pэ поясним на разрезе по плоскости, поперечной оси пути, в середине пролета, приведенном на рисунках 109 и 110.
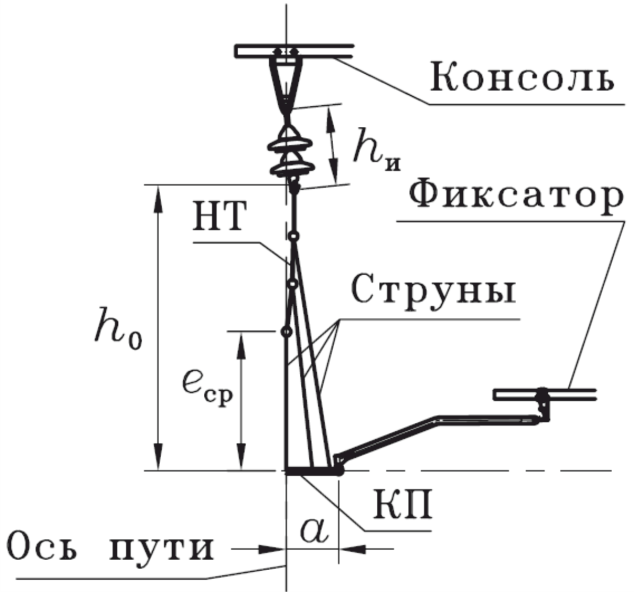
Рисунок 109 – Положение элементов полукосой КП при отсутствии ветра
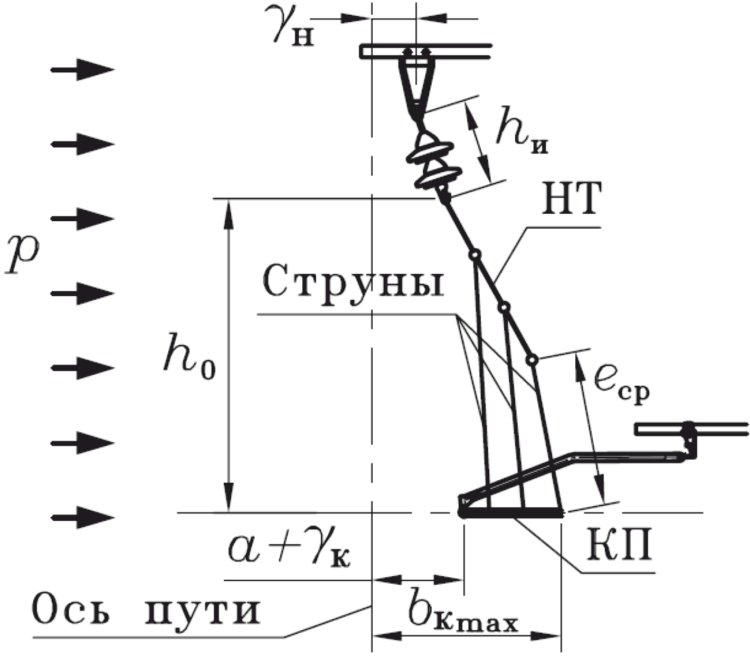
Рисунок 110 – Положение элементов полукосой КП при ветре
В выражение для lmax входят коэффициент k1 и нагрузка pэ, которые зависят от lmax. Поэтому определение максимально допускаемой длины пролета осуществляется методом последовательных приближений в следующем порядке:
1. При k1=1 и нагрузке pэ=0 определяется предварительное значение lmax.
2. Для найденной lmax определяются значения 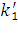 и
и 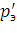 .
.
3. С учетом найденных 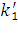 и
и 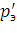 определяется уточненное
определяется уточненное 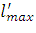 .
.
4. Если lmax и 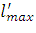 отличаются менее чем на 5%, то расчет заканчивается и значение
отличаются менее чем на 5%, то расчет заканчивается и значение 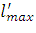 принимается в качестве окончательного, в противном случае расчет продолжается в той же последовательности до тех пор, пока это отличие не станет равным 5% и менее (при этом последнее значение длины пролета принимается в качестве окончательного).
принимается в качестве окончательного, в противном случае расчет продолжается в той же последовательности до тех пор, пока это отличие не станет равным 5% и менее (при этом последнее значение длины пролета принимается в качестве окончательного).
Точность расчета 5% рекомендуется для ручных расчетов. При расчетах на компьютерах лучше принять большую точность.
Напомним, что расчет максимально допускаемой длины пролета должен выполняться в двух режимах: РВmaxи в РГВ.
Итак, мы научились определять lmax с учетом динамических факторов на прямых участках пути при разносторонних зигзагах КП на смежных опорах, равных по величине a. Обычно зигзаги на прямых выполняются именно таким образом, a = 0.3 м (за исключением воздушных стрелок, «переходов через ноль», изолирующих сопряжений и некоторых других случаев).
Теперь рассмотрим, как определить lmax на кривых участках пути, однако вначале обсудим принципы выбора зигзагов на кривых.
Дата добавления: 2015-10-22; просмотров: 1736;
