Суммарные и результирующие нагрузки

Суммарные вертикальные и горизонтальные нагрузки в основных расчетных режимах определятся суммированием соответствующих составляющих. Например, суммарная вертикальная нагрузка на несущий трос контактной подвески от веса всех проводов с гололедом в режиме РГВ равна:

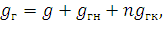
(31)

где g – вес подвески (20);

g_гн – вес гололеда на несущем тросе;

g_гк – вес гололеда на одном контактном проводе;

n – число контактных проводов.

Результирующие нагрузки определяются как векторная сумма суммарных вертикальных и горизонтальных нагрузок (см. рисунок 22 и (18)).

2.3.3. Температурные воздействия

РФ районирована на климатические зоны, по которым определяется минимальная, максимальная температуры воздуха заданной повторяемости. Максимальные температуры при расчете проводов КС и ЛЭП необходимо рассчитывать с учетом нагрева солнечной радиацией (+10..14^оC) и токами нагрузки. Допустимые температуры нагрева проводов регламентированы ПУТЭКС [5].

2.3.4. Нагрузки от проводов, передаваемые на поддерживающие и фиксирующие конструкции

На рисунке 25 приведена расчетная схема для нахождения вертикальных нагрузок, передаваемых на поддерживающие устройства.

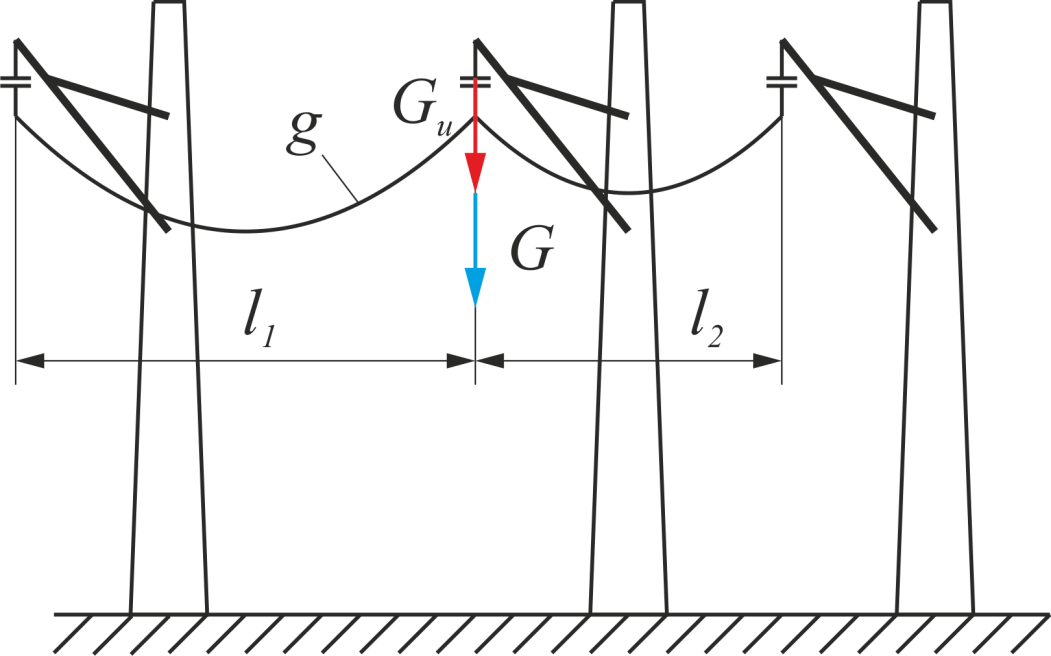
Рисунок 25 – Расчетная схема для нахождения вертикальных нагрузок; g – распределенная нагрузка на провод в соответствующем расчетном режиме, Н/м; l₁, l₂ – длины смежных пролетов, м; G_и – вес изолятора и арматуры, Н; G_и – суммарная вертикальная нагрузка, Н

Величина суммарной вертикальной нагрузки, передаваемой на поддерживающие устройства, при одинаковой высоте подвеса провода определяется по формуле

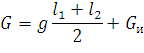
(32)

Нормативная горизонтальная нагрузка находится по формуле:

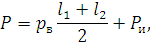
(33)

где p_в – распределенная ветровая нагрузка на провод в соответствующем расчетном режиме, Н/м;

P_и – нескомпенсированная составляющая натяжения провода при изменении его направления, Н.

На рисунке 26 приведена расчетная схема для определения P_и.

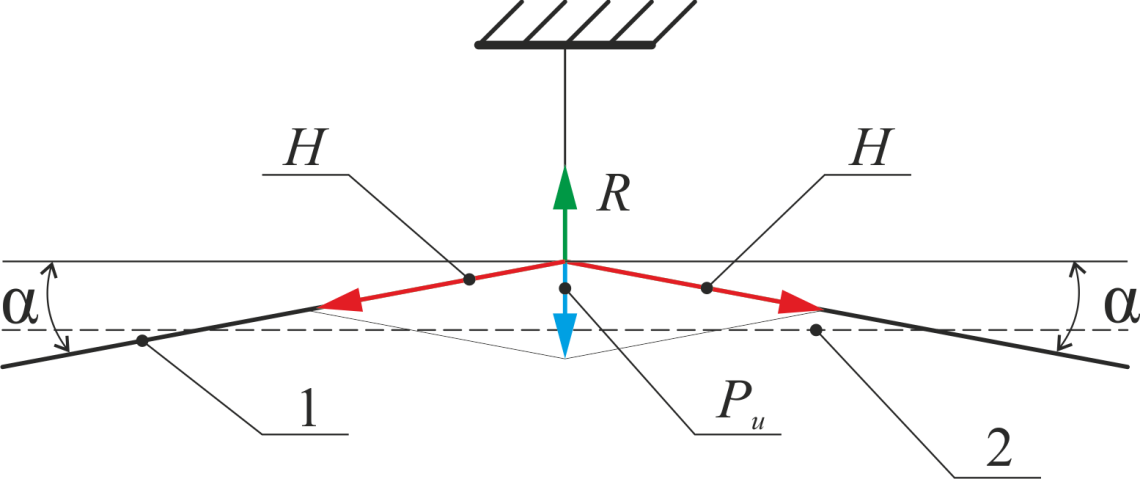
Рисунок 26 – Расчетная схема для определения P_и; 1 – КП, 2 – ось пути, α – угол наклона провода к оси пути в плане, ^оС, R – реакция фиксирующего устройства, Н

P_и определяется по формуле:

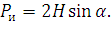
(34)

Для малых углов 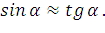В случае, когда изгиб провода вызван зигзагом на прямом участке пути можно записать

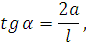
(35)

где а – зигзаг, м;

l – длина пролета, м.

Оценим величину нескомпенсированной составляющей натяжения провода, вызванную изменением его направления на прямом участке пути. Примем натяжение Н=10000 Н, зигзаг а=0,3 м, длину пролета l=60 м. Тогда:

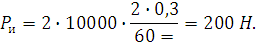
Если изгиб вызван радиусом кривой пути:

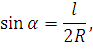
(36)

где R – радиус кривой пути, м.

Найдем P_и для кривой R=600 м, зигзага а=0,4 м, длины пролета l=60 м:

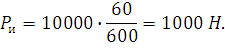
3. Расчет свободно подвешенного провода

Любой провод представляет собой растянутый стержень, опирающийся на несколько точек опор и изгибающийся под действием равномерно распределенной нагрузки от силы тяжести (собственного веса), а при ветре и гололеде – под действием соответствующих дополнительных временных нагрузок.

Расчет этого стержня будет иметь принципиально разный характер в зависимости от его жесткости и расстояния между точками, на которые он опирается.

Если длина провода незначительна, а жесткость достаточно велика, то он представляет собой балку и его расчет выполняется методами строительной механики.

При увеличении расстояния между точками опирания (длины пролета) влияние жесткости стержня на форму кривой его провисания уменьшается. В КС и ЛЭП длины пролетов, как правило, достаточно велики, жесткость стержня не оказывает существенного влияния. И в статических расчетах принимается модель проводов в виде гибкой нити, т.е. такой нити, в любом сечении которой изгибающий момент равен нулю. Такой модели также соответствует цепь с пренебрежимо малыми размерами звеньев.

3.1. Уравнение провисания провода

3.1.1. Точное уравнение провисания провода

На рисунках 27 и 28 приведены расчетные схемы для определения точного уравнения провисания провода.

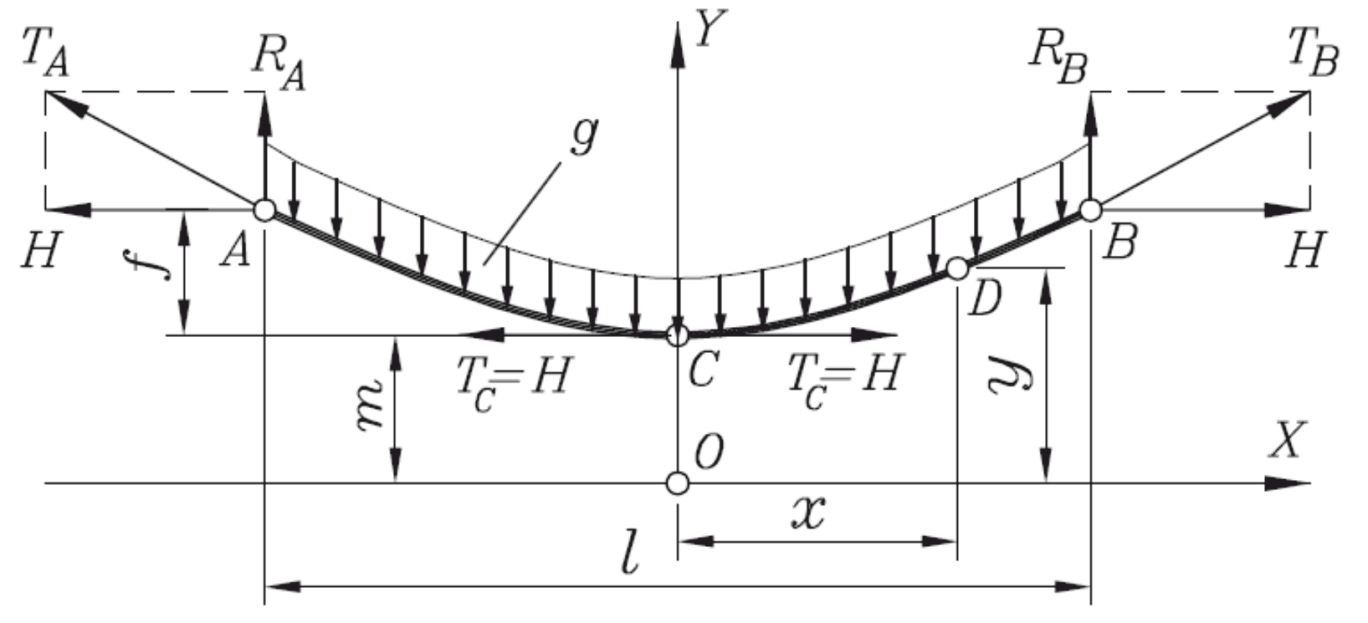
Рисунок 27 – Расчетная схема для расчета провисания гибкой линии

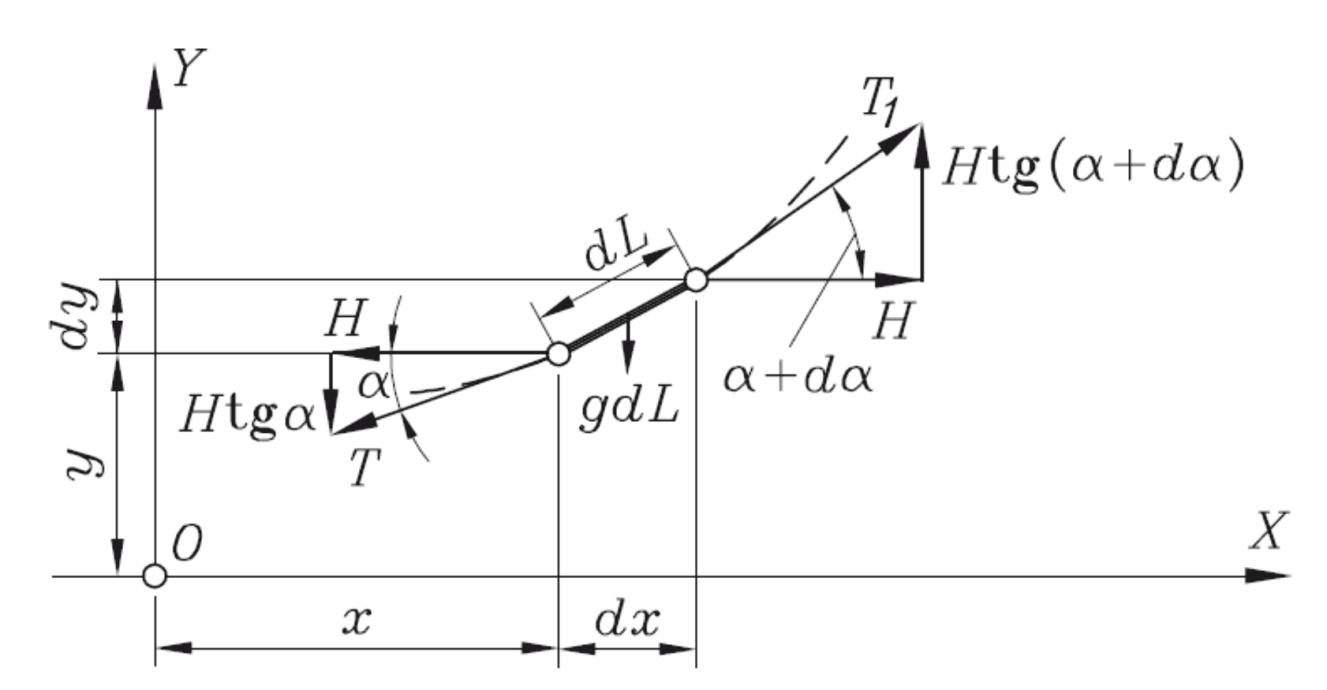
Рисунок 28 – Силы, действующие на элемент гибкой нити

Из условия равновесия элемента гибкой линии, по теореме статики, следует, что сумма всех проекций сил на оси равна нулю. Тогда из условия равенства нулю проекций сил на ось х можно записать:

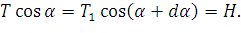
Горизонтальная составляющая натяжения по длине пролета не изменяется. Изменение полного натяжения происходит за счет вертикальной составляющей.

Т.к. сумма вертикальных проекций всех сил на ось y равна нулю, то:

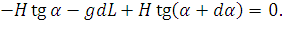
(37)

Так как 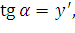то

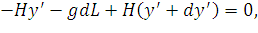
(38)

или

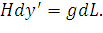
(39)

Так как

= =

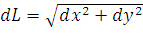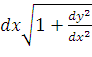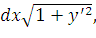
(40)

то

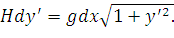
(41)

Разделив переменные, найдем:

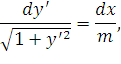
(42)

где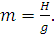

Проинтегрируем формулу (42):

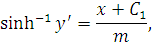
(43)

откуда

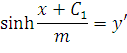
(44)

или

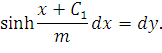
(45)

Проинтегрируем выражение (45)

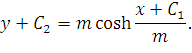
(46)

Если поместить начало координат в точку (–С₁; –С₂), уравнение (46) перепишется в виде:

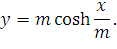
(47)

Кривая, соответствующая уравнению (47) называется цепной линией.

В новой системе координат ось ординат является осью симметрии, т.к. равные по модулю положительные и отрицательные значения x дают одно и то же значение y (cosh – четная функция).

Приняв в уравнении (47) x = 0, получим y = m т.е. y равен отрезку между началом координат и низшей точкой провисания провода.

Иногда бывает удобнее располагать начало координат в точке наибольшего провисания провода, как это показано на рисунке 29.

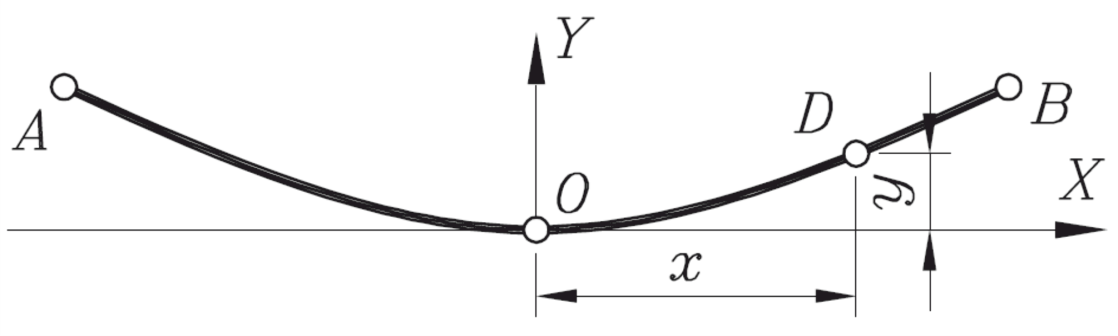
Рисунок 29 – Схема провисания гибкой нити с расположением точки начала координат в месте наибольшего провисания провода

Тогда при x = 0 и y = 0 будем иметь y’ = 0. Подставляя x = 0 в выражения (45) и (46) находим, что C₁ = 0 и C₂ = m. Подставляя эти значения в (46), получаем:

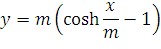
(48)

3.1.2. Приближенное уравнение провисания провода

Правую часть уравнения (48) можно разложить в ряд Маклорена:

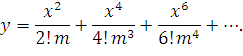
(49)

Когда пролет во много раз больше стрелы провеса, ее подсчитывают приближенно, оставляя в уравнении (49) один член. Такое упрощение позволяет представить кривую провисания провода уравнением параболы.

Подставляя m = H/g в формулу (49) получаем приближенное уравнение провисания провода:

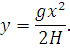
(50)

Если точки А и Б расположены на одном уровне, подставляя x = l/2 в (50), находим стрелу провеса f

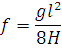
(51)

В некоторых случаях необходимо иметь уравнение провисания в системе координат с центром в точке подвеса провода, на рисунке 30 – система 01X1Y1:

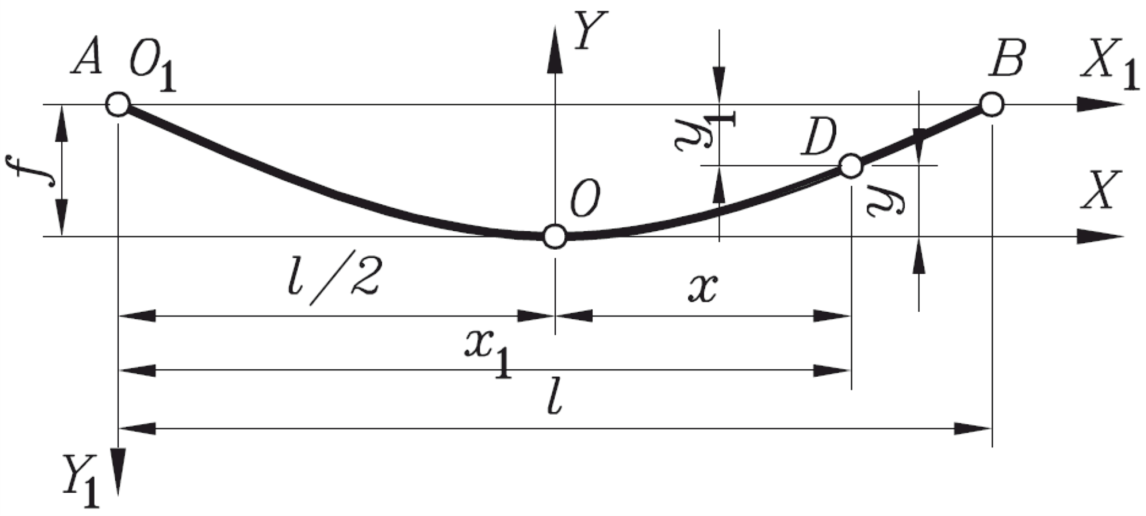
Рисунок 30 – Схема провисания гибкой нити с расположением точки начала координат в месте подвеса провода

Выполнив подстановку преобразования координат x = x₁ − l/2 и y = f − y₁ в уравнении (50), получим:

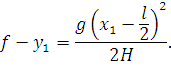
(52)

Подставив вместо f формулу (51) и упростив выражение, получим искомое уравнение провисания в системе координат 01X1Y1:

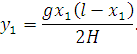
(53)

Упрощенные уравнения провисания провода по параболе обеспечивают очень хорошую точность для практических расчетов, а нередко даже оказываются ближе к реальной кривой провисания проводов, чем уравнения цепной линии (в связи с наличием у реальных проводов изгибной жесткости).

3.1.3. Упрощенный вывод приближенного уравнения провисания провода

Приближенное уравнение провисания провода может быть выведено из рассмотрения условий равновесия провода при допущении, что нагрузка пропорциональна не длине элемента, а его проекции на горизонтальную ось.

Рассмотрим отрезок нити OD, расположив начало координат в точке наибольшего провисания (см. рисунок 31).

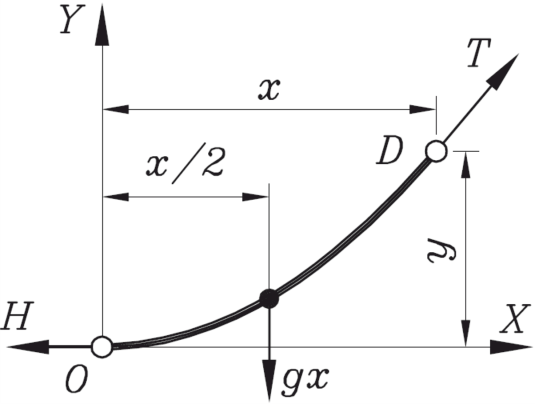
Рисунок 31 – Расчетная схема для упрощенного вывода приближенного уравнения провисания провода

Согласно нашему допущению, равнодействующая весовая нагрузка g_x прикладывается на половине отрезка x. Возьмем относительно точки D сумму моментов всех сил, приложенных к отрезку провода OD, и приравняем ее нулю (по условию равновесия)

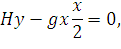
(54)

откуда

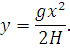
(55)

По-существу это и определяет разницу в подходах при выводе уравнения провисания гибкой нити в точной форме (цепная линия) или в приближенной (парабола). Уравнение цепной линии выводится исходя из того, что провод нагружен распределенной нагрузкой от собственного веса равномерно по длине провода, а уравнение параболы – исходя из того, что провод нагружен равномерно по длине пролета (т.е. вдоль проекции провода на горизонтальную ось). На рисунке 32 изображены кривые провисания провода для обоих случаев.

Рисунок 32 – Кривые провисания провода в точном и приближенном виде

3.1.4. Длина пролета и длина провода в пролете

На рисунке 33 изображена расчетная схема для определения длины провода в пролете.

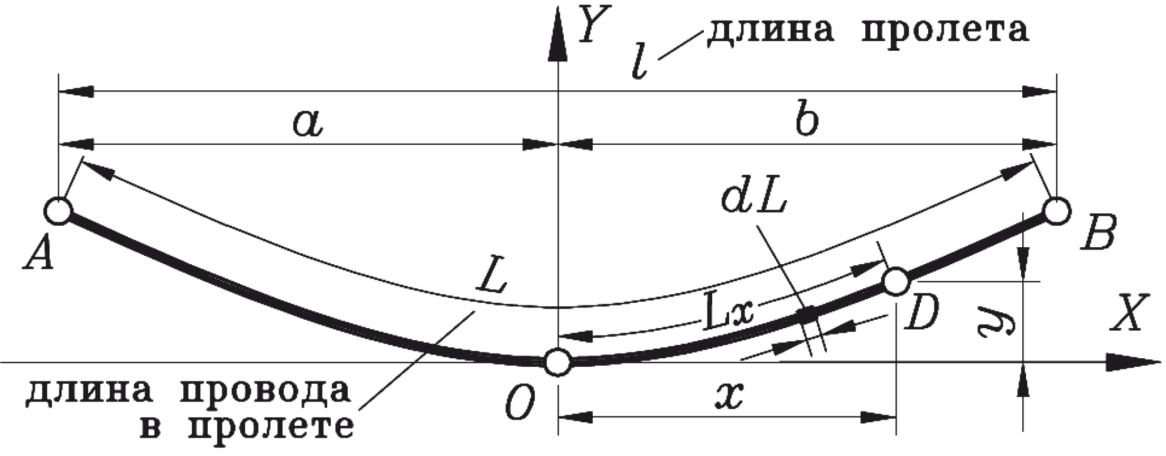
Рисунок 33 – Схема расчета длины провода в пролете

Проинтегрировав выражение (40), найдем длину провода на участке от точки O до точки D

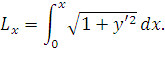
(56)

Если подставить в это выражение формулу (44) и учесть что в нашей системе координат с началом в точке наибольшего провисания C₁=0, получим:

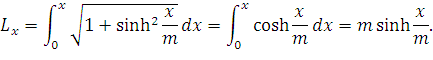
(57)

Длину между точками подвеса можно получить, заменив x один раз расстоянием от точки наибольшего провеса O до точки B, а второй раз – до точки A и сложив эти длины:

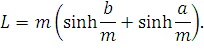
(58)

Если точки подвеса расположены на одном уровне по высоте, то a=b=l/2. Отсюда получаем уравнение для длины провода:

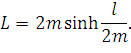
(59)

Мы получили точную формулу длины провода, провисающего по закону цепной линии при расположении точек подвеса на одном уровне.

Получим также приближенную формулу (для кривой провисания, описываемой параболой). Рассуждаем аналогично: чтобы найти длину провода, надо проинтегрировать выражение для dL. Для определения общей длины провода L при расположении точек подвеса на одном уровне возьмем интеграл с пределами интегрирования от 0 до l/2, умноженный на 2:

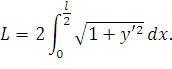
(60)

Взяв производную от (55) и подставив значение 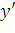в (60) получим:

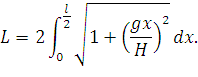
(61)

Воспользуемся тем, что 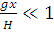, и представим подкоренное выражение в виде:

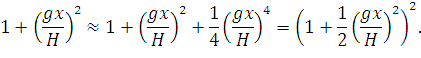
(62)

Здесь мы «произвольно» добавили к правой части малую величину. Это нам понадобилось для того, чтобы избавиться от корня. Теперь формула (61) перепишется в виде:

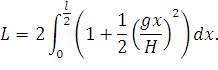
(63)

Взяв интеграл от выражения (63), получим искомую приближенную фор-

мулу для определения длины провода:

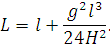
(64)

3.1.5. Приближенное уравнение провисания провода при точках подвеса, расположенных на разных уровнях

На рисунке 34 изображена расчетная схема для определения длины провода в пролете при точках подвеса, расположенных на разных уровнях.

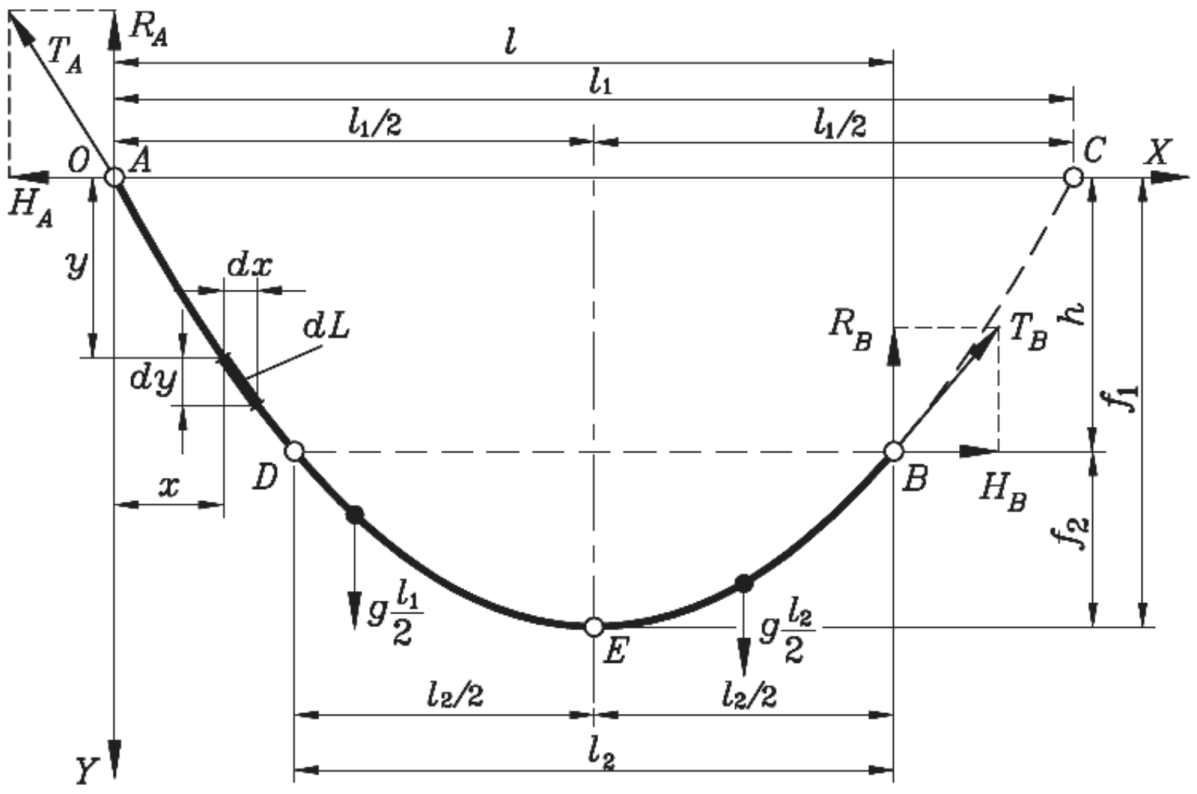
Рисунок 34 – Расчетная схема для определения длины провода в пролете при точках подвеса, расположенных на разных уровнях

Разложим на вертикальные и горизонтальные составляющие опорные реакции T_A и T_B , равные натяжению провода в точках крепления. Вертикальные и горизонтальные составляющие натяжения в точках A и B определяются из условий равновесия отрезков провода AE и BE. Заменим действие второй части провода ее реакцией. На рисунке 35 изображена схема замещения.

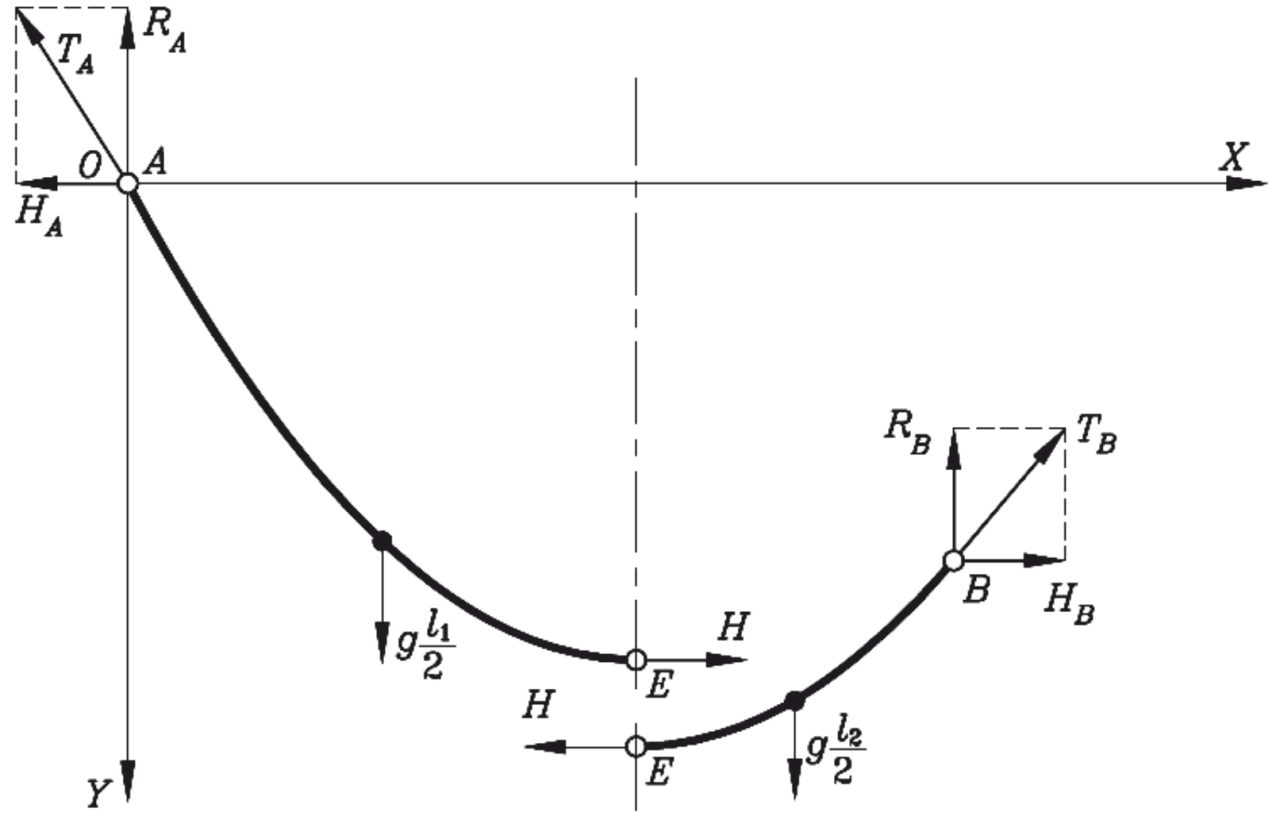
Рисунок 35 – Расчетная схема для определения длины провода в пролете при точках подвеса, расположенных на разных уровнях с заменой действия второй части провода ее реакцией

Из условия равновесия сумма проекций сил, действующих на неподвижное тело, на оси координат равна нулю. Поэтому и равенства нулю суммы проекций сил на ось х можно записать:

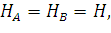
(65)

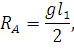
(66)

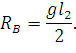
(67)

Натяжения провода в точках крепления равны:

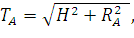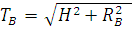
(68)

Т.е. натяжение провода в точках крепления, расположенных в разных уровнях, не одинаковое. При одинаковой величине горизонтальных составляющих оно больше в той точке, где большую величину имеет вертикальная составляющая (верхняя точка).

Продолжим кривую ADEB до пересечения с осью OX, получим точку C, расположенную на одном уровне с точкой A. Длину пролета AC обозначим l₁, а пролет DB (точка D расположена на одном уровне с точкой B) обозначим l₂. Пролеты l₁ и l₂ называются фиктивными, они дают возможность привести рассматриваемую схему к схеме расположения точек подвеса на одном уровне.

Для фиктивных пролетов, у которых точки подвеса расположены на одном уровне, справедливо выражение (51), поэтому можно записать:

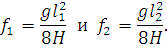
При этом:

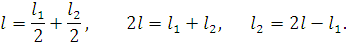
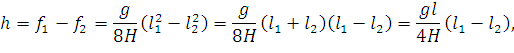
откуда:

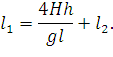
В полученное выражение подставим значение l₂ = 2l − l₁ и выразим l₁:

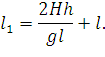
(69)

При данном расположении осей координат и точках подвеса провода, расположенных на одном уровне, уравнение кривой провисания имеет вид (53). Для пролета l₁ (кривой ADEBC) можно записать:

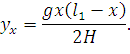
(70)

Подставим в это уравнение выражение (69).

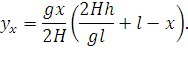
(71)

В этом выражении уже нет фиктивных длин пролетов l₁ и l₂, а есть только реальная длина пролета l. Проведя соответствующие преобразования, получим:

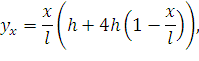
(72)

где f – провес провода в середине пролета длиной l при точках подвеса, расположенных на одном уровне, м;

x – расстояние от более высокой точки подвеса до того места, где определяется провес y_x.

Определим расстояние от более высокой точки подвеса до места, где провод занимает самое низкое положение (точка E). Для этого найдем первую производную от y_x, приравняем ее нулю и выразим х:

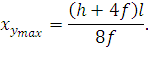
(73)

3.1.6. Длина провода в пролете при точках подвеса, расположенных на разных уровнях

Чтобы найти длину провода в пролете проинтегрируем выражение (40).

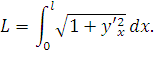
(74)

Подставим в (74) производную от (72):

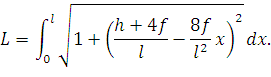
(75)

Аналогично (62) представим подкоренное выражение в виде:

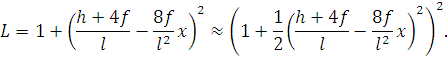
(76)

Тогда

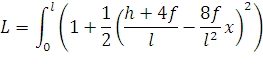
(77)

После соответствующих преобразований, имеем:

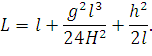
(78)

Отметим, что при h = 0 это выражение превращается в выведенное ранее выражение (64) для провода с точками подвеса, находящимися на одном уровне.

3.1.7. Стрела провеса провода при точках подвеса, расположенных на разных уровнях

Рассмотрим расчетную схему для провода с точками подвеса, расположенными на разных уровнях, в системе координат с началом в точке с максимальным провесом, приведенную на рисунке 36.

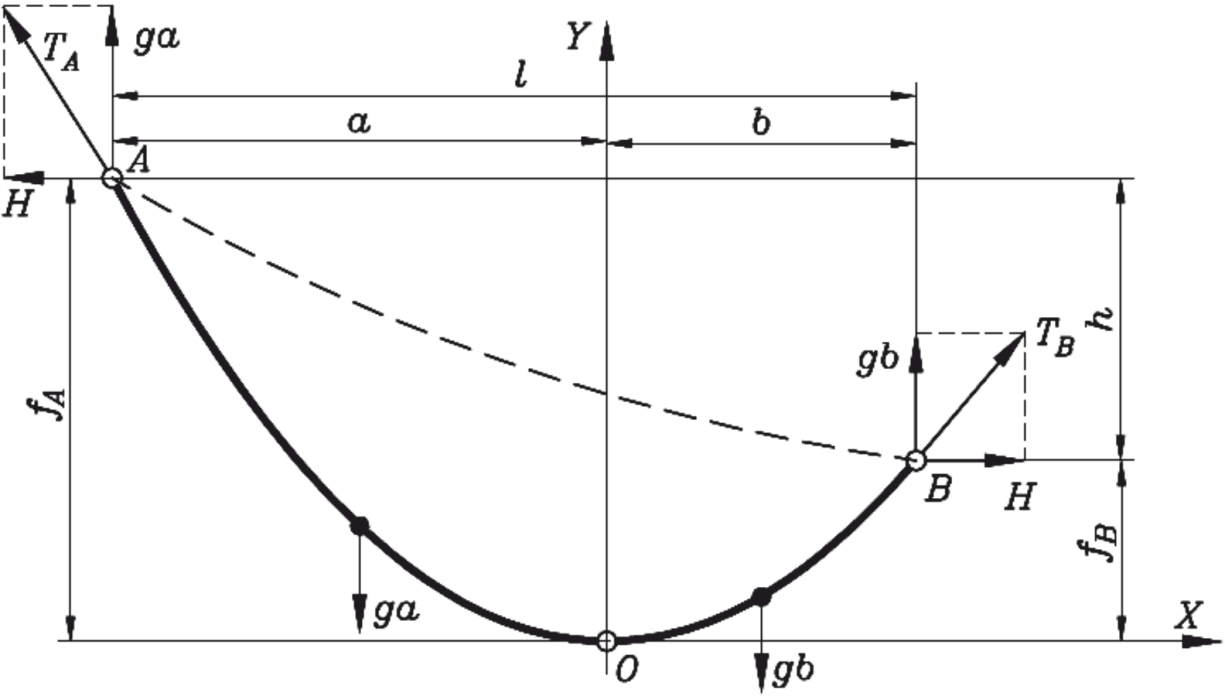
Рисунок 36 – Расчетная схема для определения стрелы провеса провода с точками подвеса, расположенными на разных уровнях

Обозначим через a и b расстояния по горизонтали от точек подвеса до точки с максимальным провесом.

Принимая нагрузку пропорциональной длине проекции провода, найдем, что равнодействующие частей AO и OB соответственно равны ga и gb.

Возьмем сумму моментов сил относительно точки B и приравняем ее нулю по условию равновесия:

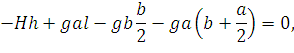
(79)

откуда:

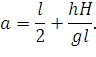
(80)

Т.к. a + b = l, то

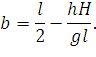
(81)

Из (80) и (81) видно, что a и b положительны и наибольший провес находится между точками подвеса, когда

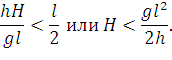
(82)

Если

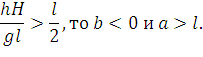
(83)

Это соответствует случаю, когда растягивающее усилие так велико, что вершина кривой провисания находится справа от точки B (штриховая линия).

Если в уравнение (3.16) подставить x = −a , а затемx = b, то соответственно:

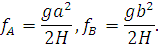
(84)

Заменим a и b их значениями из выражений (80) и (81) получим искомые выражения для стрелы провеса:

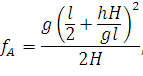
(85)

3.2. Уравнение состояния провода

При изменении температуры или изменении нагрузки на провод (например, при воздействии гололеда, ветра) изменяется его длина, и как следствие, изменяется натяжение и стрела провеса. Зная натяжение или стрелу провеса, соответствующие одному расчетному режиму необходимо иметь возможность определять натяжение или стрелу провеса, соответствующие другому расчетному режиму. Это нужно, например, для того, чтобы задавшись максимально допустимым натяжением в проводе при наиболее тяжелых для него условиях, можно было определить натяжение для всех иных режимов работы. Таким образом можно будет рассчитать натяжение и стрелу провеса при монтаже так, чтобы гарантировать, что в наиболее тяжелых условиях работы натяжение не превысит максимально допускаемое.

Уравнение, которое устанавливает зависимость между натяжениями или стрелами провеса провода в двух различных режимах называется уравнением состояния.

Будем обозначать параметры провода, соответствующие первому, исходному режиму индексами «1»:

t₁ – температура в исходном режиме (⁰C);

q₁ – распределенная линейная нагрузка на провод в исходном режиме (Н/м);

H₁ – натяжение провода в исходном режиме (Н);

f₁ – стрела провеса провода в исходном режиме (м);

L₁ – длина провода в пролете в исходном режиме (м).

Те же параметры провода, во втором, определяемом режиме будем обозначать индексами «i»: t_i, q_i, H_i, f_i, L_i.

Если считать натяжение провода неизменным, то при температуре t_i длина провода будет равна

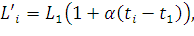
(86)

где α – температурный коэффициент линейного расширения материала провода (⁰C⁻¹).

Однако, изменение длины провода приведет к изменению стрелы провеса, а следовательно, и к изменению натяжения. Изменение натяжения изменит начальную длину L_i согласно закону Гука:

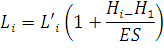
(87)

где E – модуль упругости провода, Н/мм²;

S – площадь поперечного сечения провода, мм².

В результате одновременного изменения температуры и нагрузки длина провода будет равна

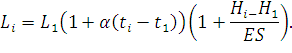
(88)

Раскроем скобки:

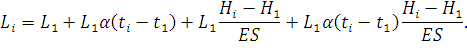
(89)

Пренебрегая последним членом уравнения как малой величиной второго порядка (произведение двух малых величин) и вычитая из обеих частей уравнения L₁, найдем удлинение провода:

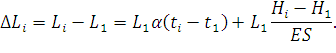
(90)

Учитывая, что длина провода незначительно отличается от длины пролета, примем для определения приращения L₁ ≈ l. Тогда

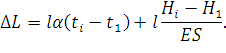
(91)

С другой стороны, приращение ∆L может быть представлено как разность между конечной и начальной длиной провода, определенными по выражению (64) (или (78) при разных высотах подвешивания):

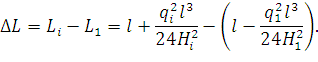
(92)

Приравняв правые части выражений (91) и (92), получим уравнение состояния провода:

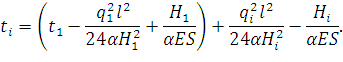
(93)

Если известно натяжение провода для какого-либо одного режима, уравнение состояния позволяет определить значение этого натяжения для любого другого режима с заданной температурой и нагрузкой.

Если в уравнении (93) заменить H_i и H₁ их значениями из выражения (51) (f=ql²/(8H)), после преобразований можно получить зависимость между стрелами провеса в двух разных режимах:

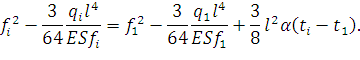
(94)

3.3. Расчеты свободно подвешенного провода при изменениях климатических условий

Основные задачи расчетов:

1. Разработка монтажных кривых и монтажных таблиц для производства монтажа и регулировки проводов при различной температуре. На рисунке 37 приведены пример монтажной кривой и монтажной таблицы.

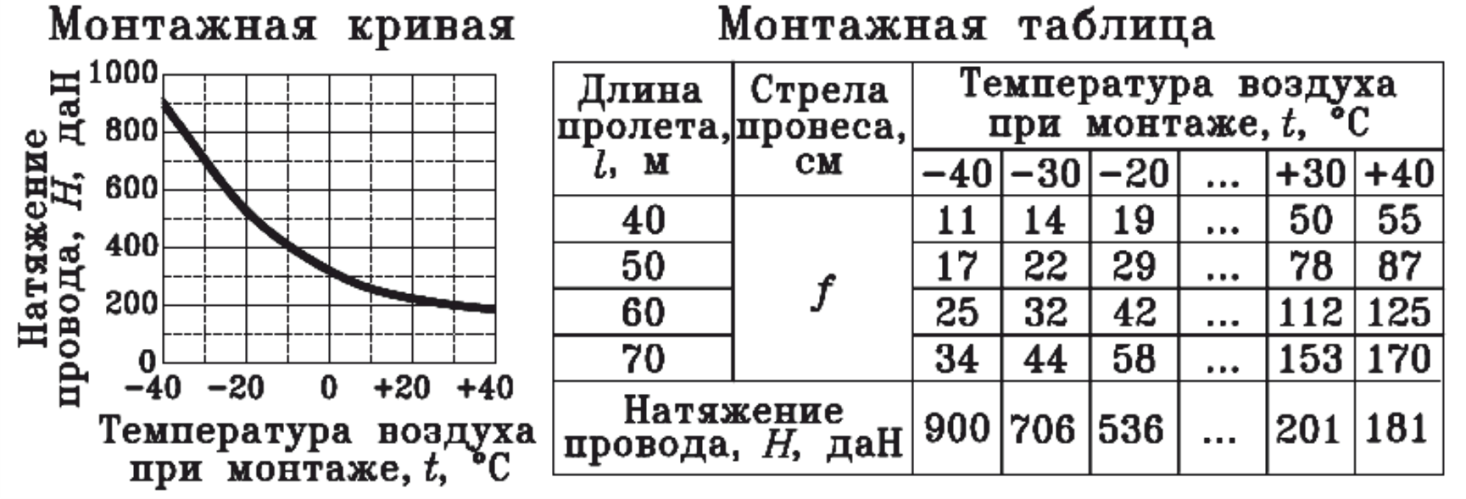
Рисунок 37 – Пример монтажной кривой и монтажной таблицы

2. Проверка соблюдения вертикальных и горизонтальных габаритных расстояний во всех условиях эксплуатации (как правило, расчеты проводят в расчетных режимах Р_tmin, Р_tmax, РГВ, РВ_max).

Например, должны контролироваться:

– расстояние до земли в точке с максимальным провесом;

– расстояние между проводами в местах их пересечения и т.д.

3. Определение натяжений провода в различных режимах. Например, это нужно для расчета нагрузок, передаваемых от проводов на поддерживающие конструкции для подбора поддерживающих конструкций и опор.

Для решения этих задач используются уравнения состояния провода и уравнения провисания.

Уравнение состояния позволяет нам определить натяжение провода в любом расчетном режиме и построить зависимость натяжения от температуры, если известны H₁, q₁ и t₁ в исходном режиме. На рисунке 38 приведен график зависимости натяжения провода от температуры в различных режимах.

Рисунок 38 – График зависимости натяжения провода от температуры в различных режимах

Отметим, что относительно Hi уравнение состояния является кубическим. Аналитическое решение его очень громоздко, поэтому обычно его решают «наоборот» – строят зависимость t_i(H_i) или решают методом «подбора» или итераций.

В качестве исходного можно принять любой режим, для которого известны H₁, q₁ и t₁. На практике в качестве исходного режима принимают такой, в котором провод будет иметь заданное проектировщиком наибольшее допускаемое натяжение H_max. В качестве H_max чаще всего принимают максимально возможное натяжение провода по прочности (с учетом коэффициентов запаса).

Однако, провод может иметь наибольшее натяжение в одном из трех расчетных режимов. На рисунке 39 изображены монтажные кривые для этих режимов.

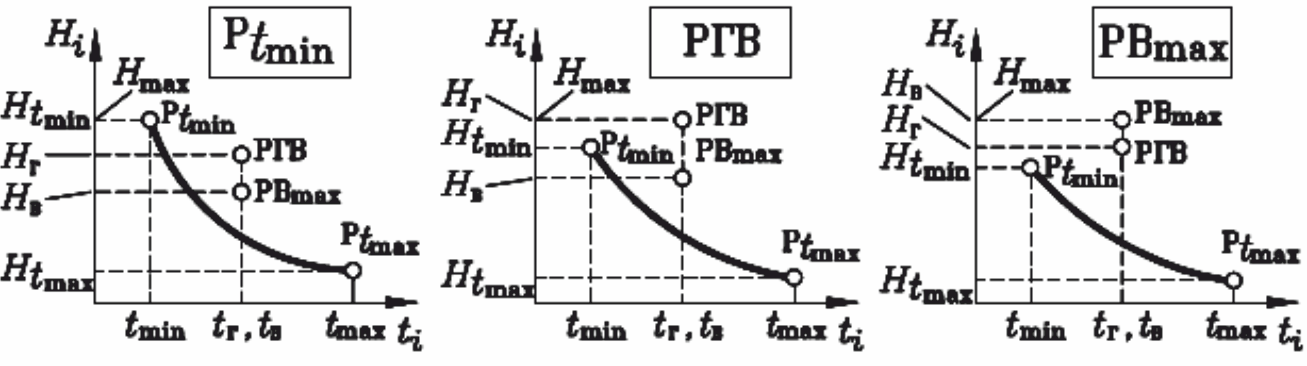
Рисунок 39 – Монтажные кривые для расчетных режимов P_tmin, РГВ, PВmax

3.3.1. Определение наиболее тяжелого (исходного) режима. Критический пролет и критическая нагрузка

В процессе эксплуатации провод может иметь наибольшее натяжение в одном из трех режимов: Р_tmin, РГВ и РВ_max.

Можно, конечно, произвольно принять один из режимов наиболее тяжелым (в этом случае натяжение провода принимается максимально допускаемым) и по уравнению состояния определить натяжение провода в двух других режимах. Затем, сравнив полученные натяжения, определить наиболее тяжелый режим.

Существует другие, более простые способы, но для этого необходимо определить критический пролет или критическую нагрузку.

Критический пролет

Критическим пролетом называется такой пролет, в котором натяжение провода как в режиме Р_tmin, так и в режиме наибольшей добавочной нагрузки (РГВ или РВmax) одинаково и равно максимально допускаемому.

То, какой режим будет наиболее тяжелым: Р_tmin или один из режимов добавочной нагрузки (РГВ и РВ_max), зависит от длины пролета. Покажем это.

Запишем уравнение состояния провода, приняв в качестве исходного режима Р_tmin, а в качестве определяемого – один из режимов добавочной нагрузки, например РГВ.

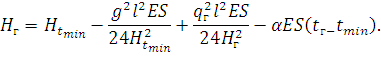
(95)

При l → 0:

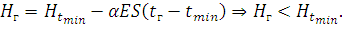
(96)

Домножим (95) на 1/l₂. При l → ∞:

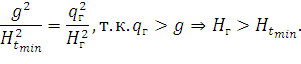
(97)

Это значит, что в коротких пролетах наибольшее натяжение провода будет в Р_tmin, а в длинных – в режиме добавочной нагрузки (данном случае – РГВ).

Следовательно, существует такой пролет, при котором H_г = H_tmin. Такой пролет называется критическим (в данном случае при совместном рассмотрении режимов Р_tmin и РГВ).

Поясним понятие критического пролета. Возьмем n пролетов разной длины. В каждом из этих пролетов при одной и той же температуре монтажа зададим одно и то же натяжение. Затем, по уравнению состояния для каждого пролета определим натяжение провода в Р_tmin, РГВ и РВ_max, и построим зависимости H_tmin(l), H_г(l), H_в(l) (см. рисунок 40).

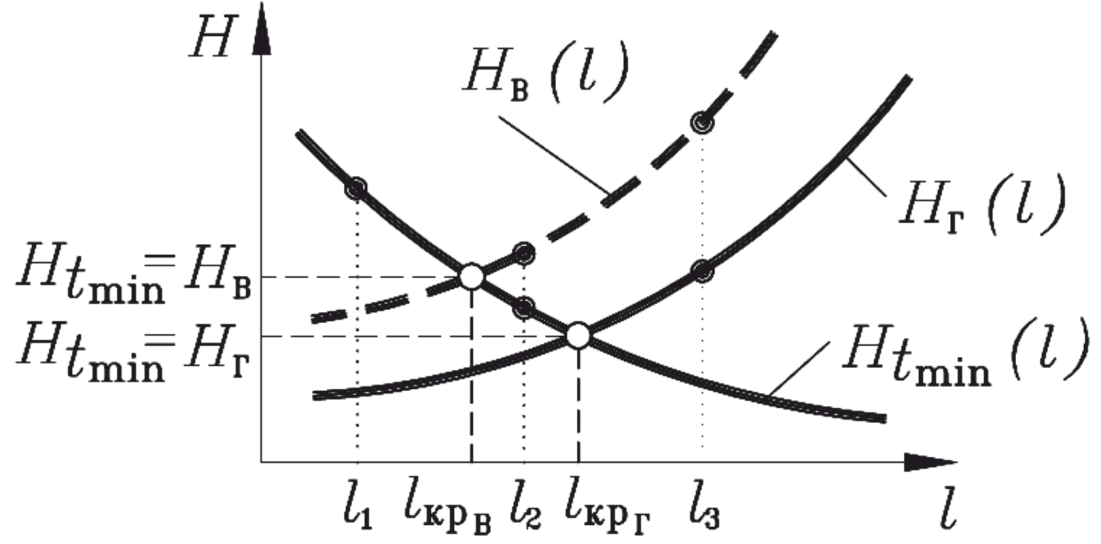
Рисунок 40 – Определение длины критического пролета

Точке пересечения кривых H_tmin(l) и H_г(l) соответствует пролет, в котором натяжения провода в Р_tmin и в РГВ одинаковы. Это и есть критический пролет при совместном рассмотрении режимов Р_tmin и РГВ.

Если известна длина критического пролета l_кр , то, сравнивая с ней длину расчетного пролета l, можно определить в каком из двух режимов Р_tmin или РГВ натяжение будет больше:

для l₁ < l₂ < l_кр наибольшее натяжение в Р_tmin,

для l₃ > l_кр наибольшее натяжение в РГВ.

Аналогично, совместно рассматриваются и режимы Р_tmin и РВ_max. Появится второй критический пролет l_кр при совместном рассмотрении режимов Р^tmin и РВ_max.

Сравнивая с l_кр длину расчетного пролета l, можно определить в каком из двух режимов Р_tmin или РВ_max будет наибольшее натяжение:

для l₁ < l_кр наибольшее натяжение в Р_tmin,

для l₃ > l₂ > l_кр наибольшее натяжение в РВ_max.

Для того чтобы определить, в каком из трехрежимов Р_tmin, РГВ или РВ_max будет наибольшее натяжение, т.е. чтобы определить наиболее тяжелый режим для провода, необходимо определить два критических пролета l_крг и l_крв и сравнить расчетный пролет с меньшим из них.

Для критического пролета при совместном рассмотрении режимов Р_tmin и РГВ l_крг натяжение в Р_tmin и РГВ равны. Если они равны максимально допускаемому, то H_г = H_tmin = H_max. Подставим H_max вместо H_г и H_tmin в (95) и получим:

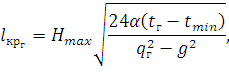
(98)

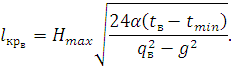
(99)