Швидкість звуку у газах

З визначенням швидкості звуку у повітрі зв'язана відома помилка Ньютона. Ньютон був упевнений, що хвильовий рух є ізотермічним процесом. Тому він вважав, що зв'язок між тиском і об'ємом повітря визначається за законом 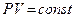, і отримав формулу

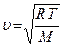. (4.4)

В цій формулі

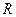- універсальна газова стала ;

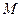- молярна маса газу;

- термодинамічна температура.

Цю помилку виправив в 1816 р. французький фізик П.Лаплас , коли встановив, що в дійсності поширення звуку є адіабатичним процесом. Це означає, що стискання й розрідження змінюються так часто, що суміжні ділянки середовища не встигають обмінюватись теплотою.

При адіабатичному процесі зв'язок між тиском і об'ємом даної маси газу дається рівнянням Пуассона:

де - показник адіабати, який показує у скільки разів молярна теплоємность газу при сталому тиску ( ) більша за молярну теплоємность при сталому об'ємі ( ).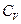

Можна теоретично довести, що тоді швидкість звуку у газах визначається за формулою:

. (4.5)

З формули (4.5 ) випливає, що швидкість поширення звуку у данному газу залежить тільки від температури.

Стоячі хвилі

Якщо в середовищі поширюються одночасно декілька хвиль, то коливання частинок середовища є геометричною сумою коливань, які здійснювали б частинки при поширенні кожної з хвиль окремо. В результаті накладання хвиль створюється деякий новий хвильовий процес. Таким процесом є, наприклад, звучання оркестру.

При накладанні хвиль можуть виникати особливі явища. Найбільш важливим із них є інтерференція хвиль. Інтерференція–це явище стійкого перерозподілу коливань у просторі, в результаті якого в одних точках коливання підсилюються, а в інших зменшуються. Інтерференція виникає коли накладаються хвилі однакових частот з незмінною різницею фаз. Такі хвилі називають когерентними.

Ми розглянемо один важливий інтерференційний ефект, який полягає в утворенні стоячих хвиль.

Стояча хвилявиникає в результаті накладання двох зустрічних когерентних плоских хвиль з однаковою амплітудою та частотою.

Практично забезпечити когерентність (узгодженість) двох джерел хвиль дуже важко. Але відомо, що при відбиванні від перешкоди виникає хвиля зустрічного напрямку поширення з такою ж самою амплітудою та частотою.

Таким чином, можна, використовуючи одне джерело плоскої монохроматичної хвилі, забезпечити когерентність хвиль, які поширюються в прямому й оберненому напрямках. Отже, практично, стоячі хвилі виникають при накладанні біжучої та відбитої хвиль.

Явища такого роду зустрічаються дуже часто. Так кожен тон звучання будь-якого музикального інструменту збуджується стоячою хвилею. Вона виникає або в струні (струнні інструменти), або в стовпі повітря (духові інструменти). Відбиваючими границями в цих випадках є точки закріплення струни та поверхні всередині духових інструментів.

Нехай дві плоскі хвилі, однакової амплітуди та частоти, поширюються назустріч одна одній. Відмінність у напрямку поширення враховується в знаках перед координатою 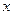в рівнянні хвилі (рис. 4.8).

Рис. 4.8

Результуюче зміщення частинок :

.

Результат виявляється дуже цікавим. Сума двох біжучих хвиль не дає хвильового руху, хоча рівняння 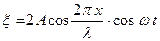називають рівнянням стоячої хвилі. Множник 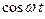показує, що в точках середовища виникають коливання з тією ж частотою 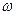, що й коливання зустрічних хвиль. Множник 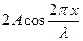, який не залежить від часу, визначає амплітуду результуючого коливання. Але амплітуда величина додатна, тому точніше амплітуда -дорівнює абсолютному значенню цього множника 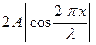. Зрозуміло, що амплітуда залежить від координати 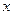, і тому в різних точках простору різна. Ця обставина є ознакою інтерференції.

Стояча хвиля не є хвилею в повному розумінні цього слова. Коли відбувається поширення біжучої хвилі, то всі частинки середовища коливаються з однаковою амплітудою і спостерігається поступова передача енергії від однієї точки простору до інших. Біжуча хвиля може рухатись праворуч, або ліворуч, але у стоячій хвилі нема напрямку поширення та передачі енергії. Назва “стояча хвиля“ характеризує просто коливальний стан середовища. Важливішою особливістю цього стану є те, що коливаються не всі частинки середовища. Це точки, координати 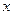яких задовольняють умові .

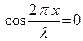Розв'язуючі це рівняння знаходимо координати нерухомих точок:

, де .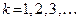

Таким чином, в точках простору, де 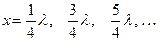коливання відсутні.

В точках простору, для яких 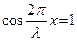амплітуда коливань максимальна.

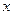Рис. 4.9

Точки простору, у яких коливання відсутні називаються вузлами стоячої хвилі, а точки, у яких амплітуда максимальна - пучностями.

На рис. 4.10 показана відмінність між поведінкою біжучої та стоячої хвилі для трьох послідовних моментів часу , , .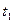

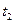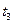Рис. 4.10

визначення коефіцієнта в’язкості біологічної рідини