Рівняння біжучої хвилі

Розглянемо простіший випадок одномірних гармонічних звукових хвиль, які збуджуються мембраною на одному з кінців довгої труби (рис. 4.4).

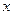Система відліку вибрана так, щоб джерело хвилі (мембрана) знаходилось в точці О, а поширення хвилі у трубі відбувалось у напрямку осі Оx. Частинки повітря позначені цифрами 1,2,3… 7. Наприклад, частинки 1 мають координату , а частинки 3 знаходяться на відстані від джерела хвилі. На рис. 4.4 показано положення частинок повітря у фіксований момент часу при відхиленні мембрани праворуч. Найбільш відхилені від положення рівноваги частинки 1, потім частинки 2 і.т.д.

Рис. 4.4

Нехай мембрана й частинки 1 коливаються за законом

,

де 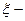зміщення від положення рівноваги;

- амплітуда коливань;

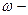частота коливань джерела хвилі (мембрани).

Якщо хвиля поширюється праворуч із швидкістю 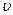, то коливання частинок 3, що розташовані на відстані 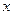будуть такими самими, але виникнуть трохи пізніше. Час запізнювання . Тому, коливання частинок, що мають координату 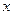, будуть здійснюватись за законом

. (4.1)

Звернемо увагу, що функція (2.1) є функцією двох змінних 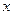і , тобто

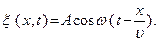(4.2)

Рівняння (4.2) називається рівнянням плоскої монохроматичної біжучої хвилі.

Ознакою монохроматичності хвилі є те, що всі частинки коливаються з однаковою частотою 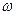. Термін - плоска хвиля означає, що всі частинки, які лежать у площині, перпендикулярній напрямку поширення хвилі (осі Ох), коливаються однаково (мають однакову фазу).

Рівняння біжучої хвилі можна подати у вигляді:

,

оскільки відомо, що 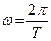, де 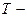період коливань. Величина дорівнює шляху, який проходить хвиля за час (час одного повного коливання). Цю величину позначають 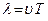, називають довжиною хвилі, а рівняння хвилі записують у вигляді

.

Величина у рівнянні є періодом коливань за часом, а величину - можна вважати своєрідним періодом у просторі. Тобто довжина хвилі - це відстань між найближчими точками у просторі, які коливаються в однаковій фазі.

Оскільки то, по аналогії, вводиться позначення 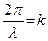. Величина 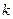-називається хвильовим числом, а рівняння біжучої хвилі набуває вигляду:

. (4.3)

Рівняння (4.2), або (4.3) визначають закон руху частинок у кожній точці простору у будь-який момент часу. Якщо у рівнянні (4.3) зафіксувати час 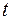(нехай, наприклад, 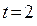), тоді функція залежить тільки від змінної . Графік цієї функції показує миттєву картину зміщень усіх частинок - як би миттєву “фотографію” хвилі (рис. 4.5)

 

 

 

Рис. 4.5

 

Важливо звернути увагу, що графік хвилі має періодичність у просторі, а періодом, дійсно, є довжина хвилі .

Поширення хвилі можна уявити, якщо переміщати цю “заморожену“ синусоїду зі швидкістю 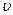вздовж осі Оx (рис. 4.6).

Дві послідовні “миттєві фотографії” хвилі у момент часу 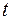і 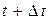показані на рис. 4.6.

 

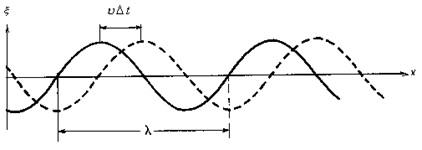Рис. 4.6

 

Рівнянням (3.3) описується не тільки відхилення положень частинок повітря від рівноваги, але і будь-яка інша величина, що аналогічно змінюється при поширенні хвилі в трубі. Наприклад, коливання тиску повітря у трубі може бути зображено у вигляді біжучої хвилі. В цьому випадку під змінною у рівнянні (4.3) слід розуміти тиск, або густину повітря (рис. 4.7).

 

Рис. 4.7