Закон сохранения количества движения (импульса)
Определение: 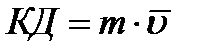 - количество движения определяет инерцию системы.
- количество движения определяет инерцию системы.
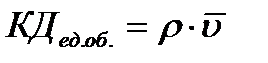
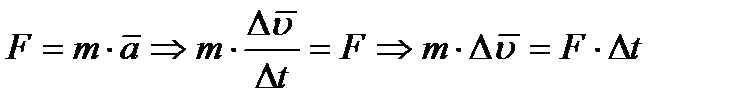
Второй закон Ньютона можно записать в форме:
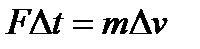 (если масса не меняется)
(если масса не меняется)
Или в более общем случае: 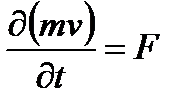
F – скорость генерации субстанции.
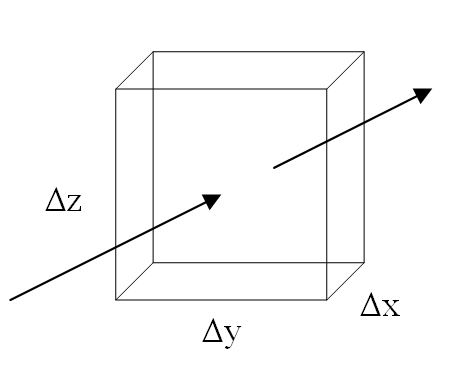
Рассмотрим движение жидкости (газа).
В общем случае изменение количества движения (КД) в элементарном объеме может происходить за счет 2-х причин:
1) разности входящего и выходящего потока количества движения, которая рассчитывается с помощью 1-го и 2-го слагаемых уравнения (1.1);
2) генерации КД, вызванной действием сил, приложенных к жидкости в элементарном объеме.
Рассмотрим действие первой причины.
КД можно считать видом субстанции. Поток субстанции через площадку S можно записать в виде:

Поток КД через площадку 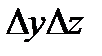 вдоль оси ОХ:
вдоль оси ОХ:
входящий:
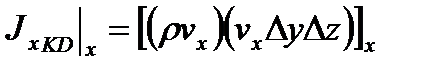
| KD в расчете на единицу объема ж-ти |
| Объем жидкости, входящий в элементарный объем |
выходящий:
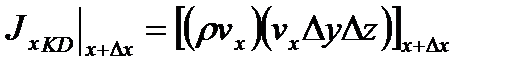
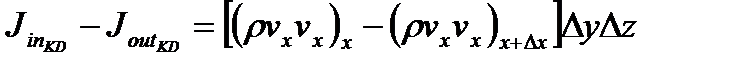
Рассмотрим вторую причину изменения КД – действие сил.
Существует два типа сил: объемные силы и поверхностные силы.
Объемные силы приложены ко всему объему: сила гравитации (ρg), электрическая сила, если объем заряжен (qE).
Поверхностные силы действуют на поверхность тела: сила давления 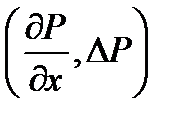 , силы трения или внутреннего напряжения.
, силы трения или внутреннего напряжения.
В общем случае к разным поверхностям, ограничивающим тело, могут быть приложены разные напряжения.
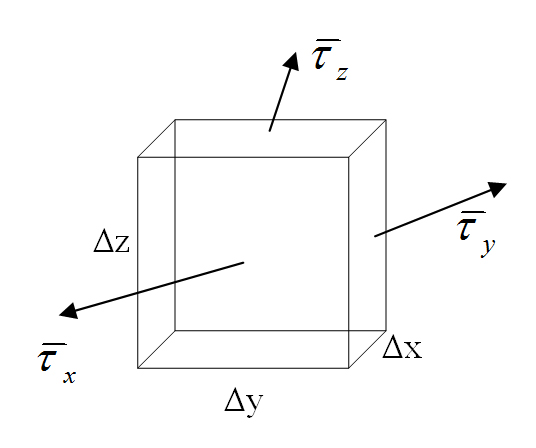
Напряжение – это вектор. Он имеет свои составляющие, направленные по осям Оx, Оy и Оz. Например, напряжение, приложенное к плоскости, перпендикулярной оси Ох:
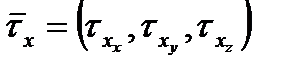
имеет координаты 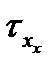 ,
, 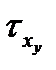 и
и 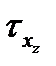 . Совокупность трех векторов, описывающих напряжения, приложенные к трем плоскостям, ограничивающим элементарный объем, называется тензором. Для того, чтобы описать тензор, надо задать 3 вектора, или 9 скалярных чисел:
. Совокупность трех векторов, описывающих напряжения, приложенные к трем плоскостям, ограничивающим элементарный объем, называется тензором. Для того, чтобы описать тензор, надо задать 3 вектора, или 9 скалярных чисел:
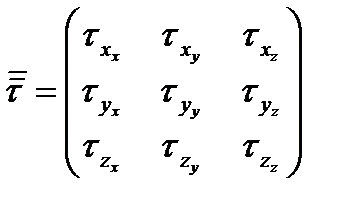
Первый индекс обозначает площадку, а второй – ось, на которой берется проекция вектора.
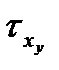 - рассматривается площадка, перпендикулярная оси Ox и берется проекция вектора, приложенного к этой площадке, на ось Oy.
- рассматривается площадка, перпендикулярная оси Ox и берется проекция вектора, приложенного к этой площадке, на ось Oy.
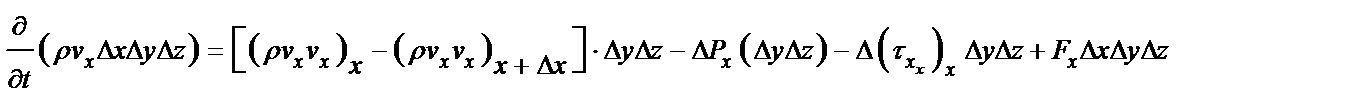
| Ск-ть прироста KD в расчете на единицу объема |
| Прирост KD за счет изменение давления на длине Δx |
| Прирост KD за счет внутренних сил трения или напряжения |
| Прирост KD за счет объемных сил |
| Прирост KD за счет конвективного переноса |
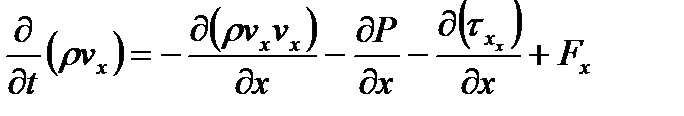
В общем случае можно получить следующее уравнение, при условии, что жидкость несжимаема ( 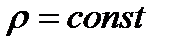 →
→ 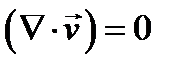 ):
):
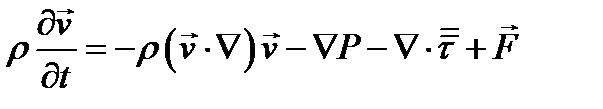
| (1.7) |
Уравнение (1.7) называется уравнением динамики сплошной среды в напряжениях.
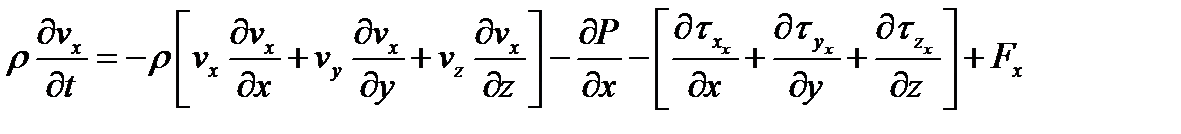
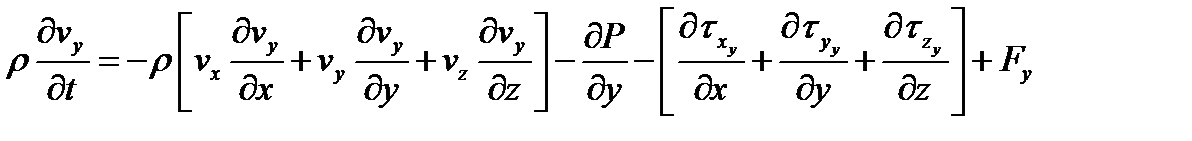
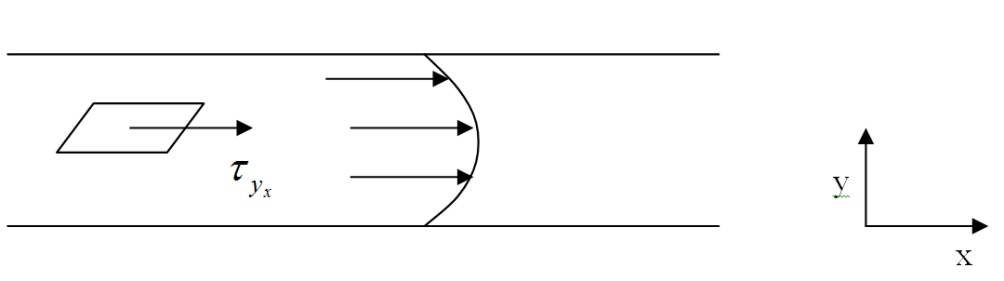
Рассмотрим плоскость вдоль оси Ox. Для ньютоновских жидкостей справедливо следующее реологическое уравнение:
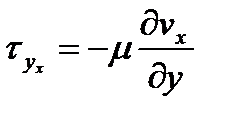
| (1.8) |
где μ – динамическая вязкость жидкости. (Ур.(1.8) можно интерпретировать т.о.: сила трения между двумя параллельно движущимися слоями жидкости пропорциональна разности скоростей движения этих слоев и обратно пропорциональна толщине прослойки между ними.)
Подставим (1.8) в(1.7):
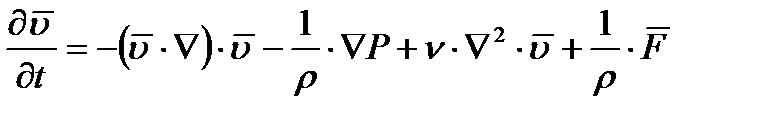 , ,
| (1.9) |
где 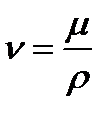 - кинематическая вязкость
- кинематическая вязкость
(1.9)- уравнение Навье – Стокса.
Задача 1: выписать уравнение Навье - Стокса в проекциях на оси x, y, z.
Уравнение Навье-Стокса в векторной форме:
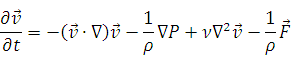
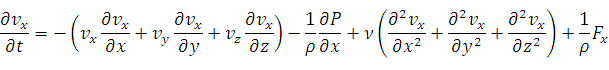
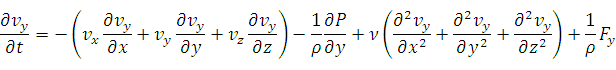
Задача. Вывести уравнение Пуазеля – распределение скоростей течения жидкости между двумя параллельными пластинами.
Принять, что течение является стационарным, установившимся, ламинарным, и на поверхности стенки выполняется условие прилипания. Объемными силами пренебречь.
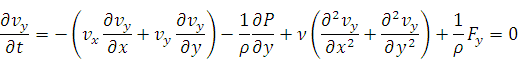
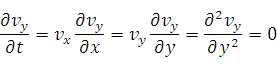
1. Стационарность течения дает условие:
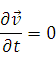
2. Ламинарное течение: 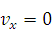 . Жидкость течет параллельно стенкам, слоями.
. Жидкость течет параллельно стенкам, слоями.
3. Установившееся течение:
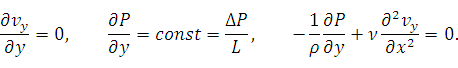
Давление – является линейной функцией от продольной координаты.
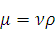
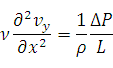
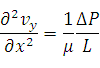
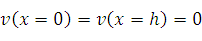 – условие прилипания.
– условие прилипания.
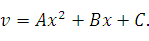
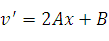
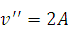
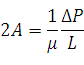
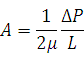
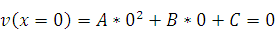
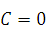
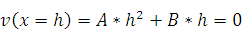
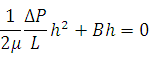
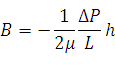
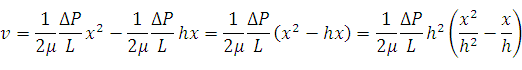
Введем безразмерную координату: 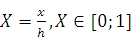 .
.
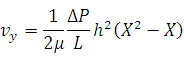
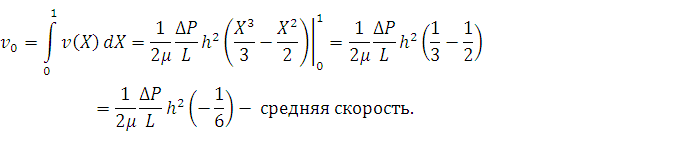
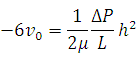
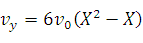
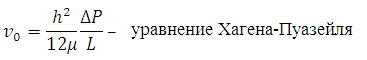
Для круглой трубы с радиусом a
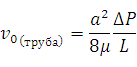
Задача
Дачник собирается купить шланг для полива. Давление воды в водопроводе равно 3 бар. Максимальная длина шланга 30 м. Дачник хочет иметь такой расход, чтобы ведро воды (10 л) наполнялось за 10 с. Какой радиус должен иметь шланг?
(Кинематическая вязкость воды)
Дано:
Давление воды на входе шланга: p = 3 бар.
Давление воды на выходе = 1 атмосфера ≈ 1 бар = 1  105
105 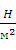 = 105
= 105  = 105
= 105 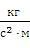
Δp = 3 бар – 1 бар = 2 бар.
L = 30 м
V = 10 л = 10  10-3 м2
10-3 м2
Кинематическая вязкость воды 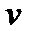 = 0,01
= 0,01 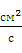 = 10-2
= 10-2  10-4
10-4 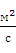
Плотность воды ρ = 103 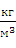
Решение:
Воспользуемся уравнением Хагена-Пуазейля для круглой трубы:
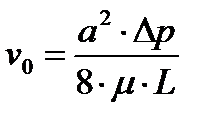 , где
, где 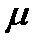 - динамический коэффициент вязкости. Выразим
- динамический коэффициент вязкости. Выразим 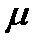 - из уравнения:
- из уравнения: 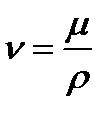 , где ν – кинематический коэффициент. Получим:
, где ν – кинематический коэффициент. Получим: 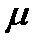 = ν
= ν  ρ = 10-3
ρ = 10-3 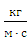
По условию, расход воды: Q = 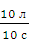 =
= 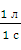 .
.
Расход воды выражается формулой: Q = 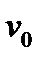
 S =
S = 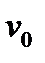

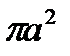 , где
, где 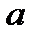 - радиус сечения шланга; S – площадь поперечного сечения шланга.
- радиус сечения шланга; S – площадь поперечного сечения шланга.
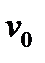 =
= 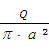 =
= 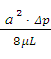 . Выразим Q, получим: Q =
. Выразим Q, получим: Q = 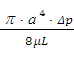 . Выразим
. Выразим 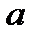 :
:
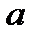 4 =
4 = 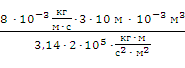 =
=  =
= 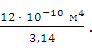
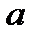 =
= 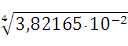

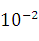 м ≈ 0,44
м ≈ 0,44 
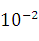 м = 0,44 см.
м = 0,44 см.
Ответ: 0,044м
Дата добавления: 2015-10-21; просмотров: 1376;
