Гидродинамическое сопротивление движению жидкости

При движении жидкости или газа в канале или при обтекании препятствия поток жидкости или газа испытывает сопротивление своему движению за счет сил трения или вязкостных сил.

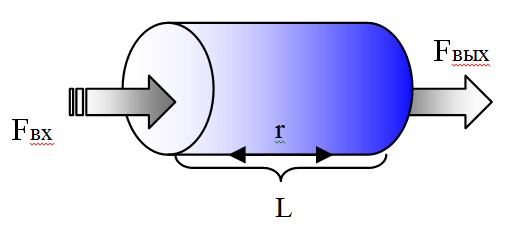
Пусть разность давлений на входе и выходе из трубы длиной L равна 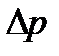. Тогда внешняя сила, действующая на жидкость и вызывающая ее течение по трубе:

,

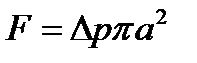где а – радиус трубы, а 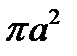– ее поперечное сечение.

Сила, действующая на единицу поверхности тела, носит название касательного напряжения 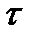(Н/м²). Полное сопротивление течению, обусловленное внутренними силами трения, равно:

,

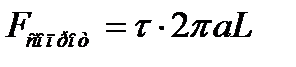где 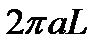– площадь внутренней поверхности трубы.

Если течение стационарное (жидкость течет без ускорения), то сила сопротивления равна действующей силе и

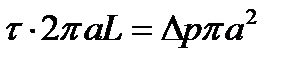
откуда ,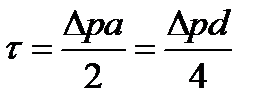

где d – диаметр трубы.

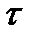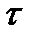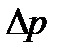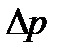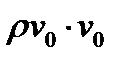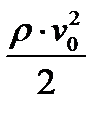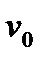Касательное напряжение характеризует силу сопротивления течению в расчете на единицу внутренней поверхности. тем больше, чем больше перепад давления . Но вместе с ростом растет и скорость переноса жидкости, которую в гидродинамике характеризуют плотностью потока количества движения или скоростным напором набегающего потока , где - средняя скорость (иначе, 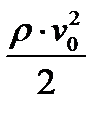есть кинетическая энергия единицы объема жидкости).

Отношение учетверенной удельной силы сопротивления (касательного напряжения 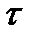) к скоростному напору набегающего потока называется коэффициентом сопротивления :

,

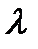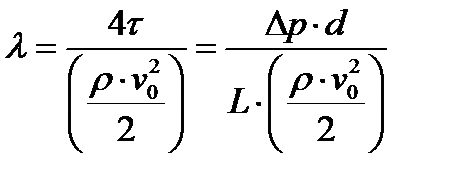(1.10)

Согласно уравнению Хагена-Пуазейля для круглой трубы,

,

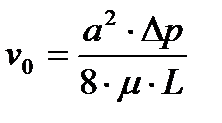(1.11)

где 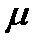- динамический коэффициент вязкости, который связан с кинематическим коэффициентом 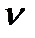уравнением: .

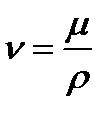Из уравнения (1.11) можно выразить 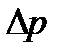и подставить в уравнение (1.10):

,

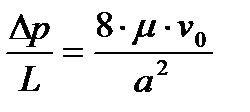
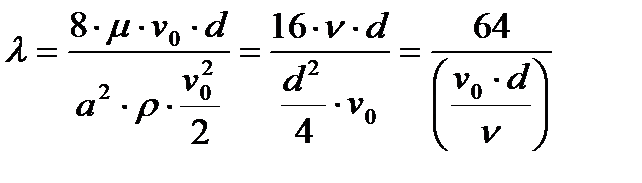
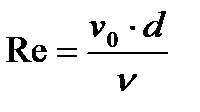(1.12)

число Рейнольдса для трубы.

Тогда 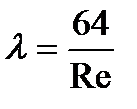- коэффициент сопротивления для трубы.

Рассмотрим плоскую щель: две пластины, между которыми течет жидкость, расстояние между ними .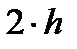

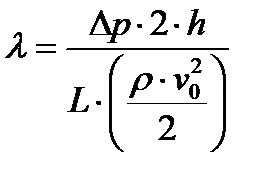,	(1.13)
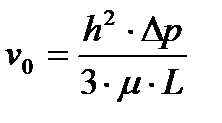,	(1.14)

Из (1.14) выражаем 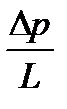и подставляем в (1.13), получим:

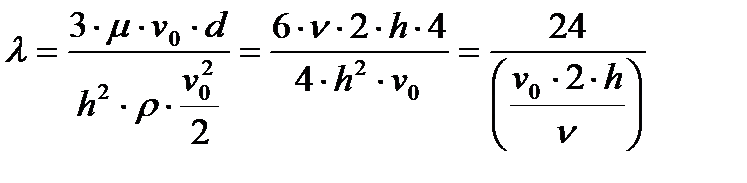
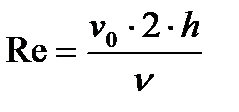, - число Рейнольдса для плоской щели

(1.15)

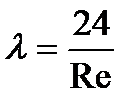- коэффициент сопротивления для плоской щели.

В общем виде коэффициент сопротивления .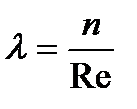

Замечание:формулы (1.11) и (1.14), (1.12) и (1.15) справедливы для ламинарного течения жидкости.

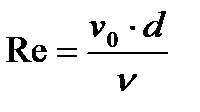, это число можно интерпретировать как отношение сил инерции к вязкостным силам.