Уравнение сохранения массы (уравнение непрерывности среды)

Пусть 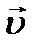- скорость центра масс, 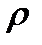- плотность жидкости, тогда плотность потока:

.

,

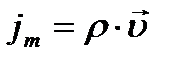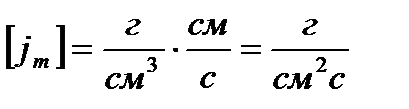
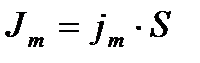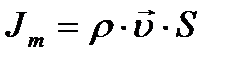- полный поток через всю поверхность.

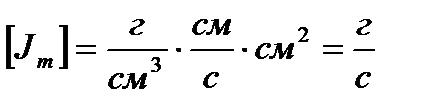
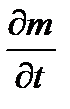- скорость прироста массы в элементарном объеме.

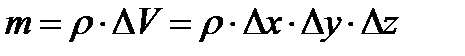- масса частиц в объеме .

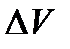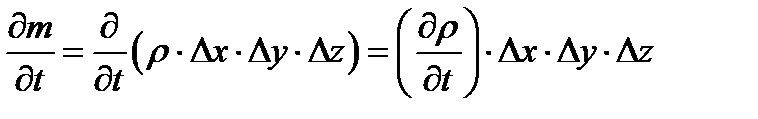- это левая часть уравнения (1.1)

(1.2)

Потоки вдоль оси Ох:

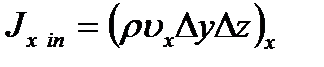суммарный входящий поток	(1.3)
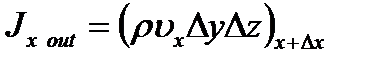суммарный выходящий поток	(1.4)

Возникновение или исчезновение массы происходит только в процессе ядерных реакций. В данном курсе мы не будем рассматривать такие реакции, поэтому в правой части уравнения (1.1) второе и третье слагаемые будут равны нулю.

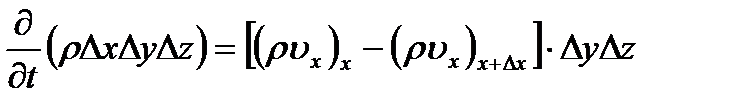
Разделим обе части уравнения на :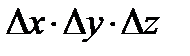

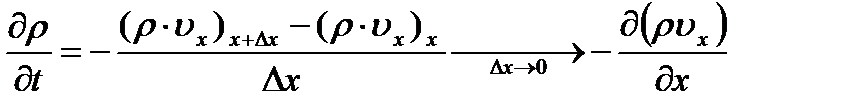- движение вещества вдоль оси Ох, 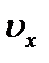- проекция скорости на ось Ох.

В общем случае

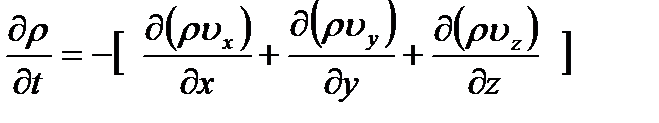
Определение дивергенции вектора : .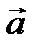

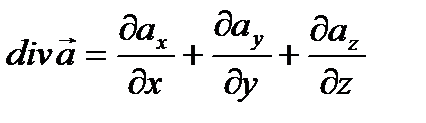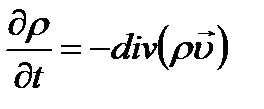
Другая запись:

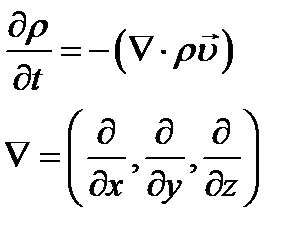
В случае несжимаемой жидкости 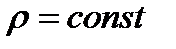, тогда 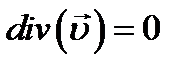или

,

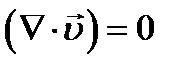(1.5)

Это уравнение непрерывности (неразрывности) сплошной среды.

Дивергенция вектора скорости или скалярное произведение оператора набла и скорости равны нулю.