Инерционные звенья второго порядка
Его уравнение: T12p2y + T2py + y = ku.
Передаточная функция:W(p) = 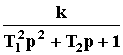 .
.
Решение уравнения зависит от соотношения постоянных времени T1 и T2, которое определяет коэффициент затуханияr = 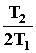 . Можно записать W(p) =
. Можно записать W(p) = 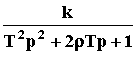 , где T = T1.
, где T = T1.
Если r 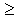 1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается на два сомножителя:
1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается на два сомножителя:
T2p2 + 2rTp + 1 = T2 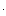 (p - p1).(p - p2).
(p - p1).(p - p2).
Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.
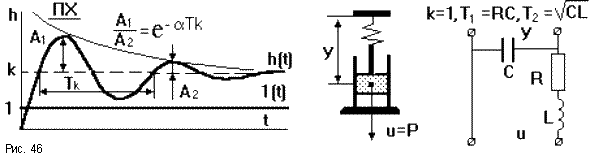
При r<1 корни полинома знаменателя W(p) комплексно сопряженные: p1,2 = 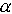 ± j
± j  . Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с затуханием
. Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с затуханием 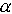 и частотой
и частотой  (рис.46). Такое звено называется колебательным. При r = 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называется консервативным. Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство, электрический колебательный контур с активным сопротивлением и т.п. Зная характеристики реального устройства можно определить его параметры как колебательного звена. Передаточный коэффициентk равен установившемуся значению переходной функции.
(рис.46). Такое звено называется колебательным. При r = 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называется консервативным. Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство, электрический колебательный контур с активным сопротивлением и т.п. Зная характеристики реального устройства можно определить его параметры как колебательного звена. Передаточный коэффициентk равен установившемуся значению переходной функции.
Дата добавления: 2015-10-19; просмотров: 707;
