Инерционное звено первого порядка (апериодическое)

Уравнение динамики: 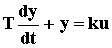, или Tpy + y = ku.

Передаточная функция: W(p) = .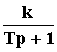

Переходная характеристика может быть получена с помощью формулы Хевисайда:

,

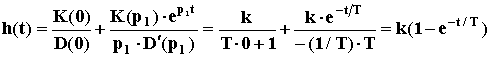где p₁ = - 1/T - корень уравнения D(p) = Tp + 1 = 0; D’(p₁) = T.

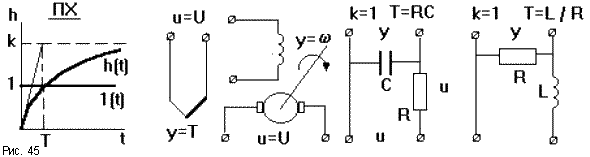
Переходная характеристика имеет вид экспоненты (рис.45), по которой можно определить передаточный коэффициент k, равный установившемуся значениюh(t), и постоянную времени Т по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно больших Т звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное. Примеры апериодического звена: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.