Безинерционные (усилительные или статические) звенья.
К безинерционным звеньям относят элементы, которые в динамике описываются дифференциальным уравнением нулевого порядка вида
yвых(t) = kхвх(t), (1)
где k-статический коэффициент передачи звена.
Для получения выражения передаточной функции запишем уравнение (1) в операторной форме (на основании основного свойства преобразования Лапласа: 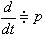 )
)
yвых(p) = kxвх(p)
По определению передаточная функция находится как отношение выхода ко входу в операторной форме при нулевых начальных условиях:
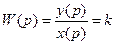 (2)
(2)
Из передаточной функции найдем статический коэффициент передачи звена (в статике все производные равны 0)
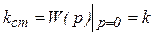
Выражение передаточной функции совпадает со статическим коэффициентом передачи, поэтому звено называют статическим.
Из передаточной функции находят переходную и весовую функции в операторной форме:
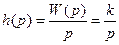 (3)
(3)
Оригинал переходной характеристики находят из таблиц преобразования Лапласа.

Переходная характеристика безинерционного звена имеет вид:
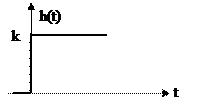 |
 |
Весовая функция в операторной форме
ω(p)=W(p) (4)
Оригинал весовой функции
ω(t) = L-1 {k } = k d(t)
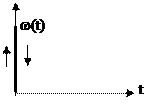 | |||
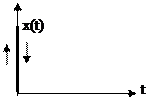 | |||
δ(t)- дельта-функция импульс бесконечно малой длительности и бесконечно большой амплитуды, площадь которого равно 1.
Частотные характеристики звена найдем из выражения комплексной передаточной функции:
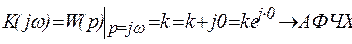 (5)
(5)
Амплитудно-частотная и фазо-частотная характеристики звена имеют вид:
АЧХ: 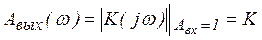
ФЧХ: 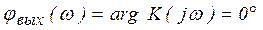
Графическое изображение частотных характеристик представлено на рисунках:
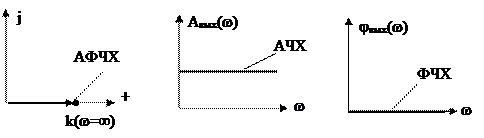 |
АФЧХ- годограф вектора K(jw) в комплексной плоскости при изменении частоты от 0 до 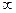 .
.
Дата добавления: 2015-09-28; просмотров: 1235;
