Модели статики. Понятие о линейных элементах. Линеаризация реальных элементов САР, её способы и предпосылки.

Статикой называется установившийся режим звена или системы, при котором входной и выходной сигналы звена (или системы) постоянны во времени.

Поведение звена (системы) в статике наглядно отражается его статическойхарактеристикой, под которой понимается зависимость между установившимися значениями выходной и входной величин.

yвых. уст. = f(xвх. уст.)

По виду статической характеристики различают линейные и нелинейные звенья. Статическая характеристика линейного звена представляет собой уравнение прямой линии:

yвых= kxвх+ yo ,

где k= tgα

Звенья, статические характеристики которых не являются прямыми линиями, называются нелинейными.

В основном все звенья в природе являются нелинейными.

Вопрос линейности статических характеристик имеет чрезвычайно важное значение. Дело в том, что в динамике САР описываются дифференциальными уравнениями. И если в САР входит нелинейное звено, дифференциальное уравнение получается нелинейным. Решение нелинейных дифференциальных уравнений – процесс трудоёмкий и сложный. Поэтому на практике нелинейные элементы заменяют их линейными моделями для облегчения их описания. Этот процесс называется линеаризацией. Итак, линеаризация нелинейного звена – замена его линейной моделью с сохранением основных свойств нелинейного звена. Простейшими методами линеаризации являются метод касательной, метод секущей и кусочно–линейная линеаризация.

При линеаризации касательной полагают, что в процессе работы объекта рабочая точка статической характеристики будет совершать лишь незначительные колебания вокруг номинального режима и, следовательно, характеристику можно заменить касательной к характеристике в точке А (системы стабилизации).

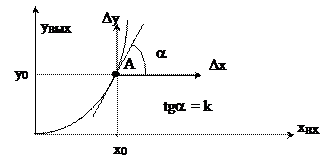
Для получения уравнения касательной перенесем начало координат в точку А и запишем уравнение касательной в отклонениях от точки номинального режима:

Dу = kDх

Величина 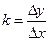- отношение выходной величины к входной – статический коэффициент передачи. Для нелинейных звеньев “к” – величина не постоянная и зависит от положения рабочей точки А.

Метод секущей, может быть, применим к объектам, имеющим нелинейную статическую характеристику, кососимметричную относительно начала координат.

Характеристику такого типа можно заменить линейной секущей АА, причём провести её нужно так, чтобы ошибки ∆ _1, ∆ _2, ∆ _3, ∆ ₄были минимальными.

Метод кусочно-линейной линеаризации применим для нелинейных объектов, статические характеристики которых могут быть представлены в виде отдельных отрезков прямой линии (1, 2, 3, 4, 5).

Для каждого отрезка характеристики справедливо линейное дифференциальное уравнение. Переход от одного участка к другому осуществляется «припасовыванием» отдельных решений. При этом решение для конца одного участка является начальным условием для следующего и т.д.

В статике все звенья можно разделить на два больших класса: статические и астатические. Статические звенья – звенья, поведение которых в статике описывается статической характеристикой типа y_вых= kx_вх

Существует большой класс звеньев, для которых статическую характеристику не удается получить, т.е. в зависимость y_вых = f (x_вх) входит время. Такие объекты называются астатическими. Условно в качестве статической характеристики для астатических звеньев считают зависимость: 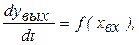т.е. в астатических объектах каждому значению входного сигнала соответствует определенная скорость входного сигнала.