Основные определения и геометрические трактовки
Комплексным числом zназывается выражение следующего вида
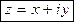
где x, y Î 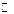 , i — это мнимая единица, определяемая равенством
, i — это мнимая единица, определяемая равенством 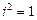 .
.
Основные термины:
x = Re z — действительная часть комплексного числа z;
y = Im z — мнимая часть комплексного числа z;
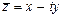 — комплексно сопряженное число числу z;
— комплексно сопряженное число числу z;
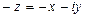 — противоположное число числу z;
— противоположное число числу z;
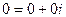 — комплексный ноль;
— комплексный ноль;
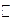 – так обозначается множество комплексных чисел.
– так обозначается множество комплексных чисел.
Примеры (комплексные числа)
1) z = 1 + i Þ Re z = 1, Im z = 1, 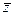 = 1 – i,
= 1 – i, 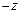 = –1 – i;
= –1 – i;
2) z = –1 + 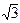 i Þ Re z = –1, Im z =
i Þ Re z = –1, Im z = 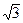 ,
, 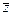 = –1 –
= –1 – 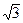 i,
i, 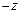 = –1 –
= –1 – 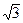 i;
i;
3) z = 5 + 0i = 5 Þ Re z = 5, Im z = 0, 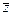 = 5 – 0i = 5,
= 5 – 0i = 5, 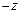 = –5 – 0i = –5
= –5 – 0i = –5
Þ если Im z = 0, то z = x — действительное число;
4) z = 0 + 3i = 3i Þ Re z = 0, Im z = 3, 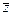 = 0 – 3i = –3i,
= 0 – 3i = –3i, 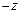 = –0 – 3i = – 3i
= –0 – 3i = – 3i
Þ если Re z = 0, то z = iy — чисто мнимое число.
Комплексные равенства
Равенство двух комплексных чиселозначает равенство дейсствительных частей и равенство мнимых частей этих чисел; равенство комплексного числа нулюозначает, что действительная и мнимая части этого числа равны нулю.
1)  2)
2) 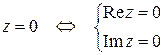
Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства процедурой, которая называется разделением действительных и мнимых частей в комплексном равенстве.
Например, 1) 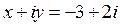
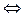
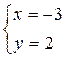 ;
;
2) 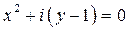
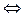
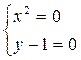
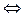
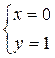 .
.
Геометрическое изображение комплексных чисел
Любое комплексное число z изображается на комплексной плоскости точкой 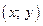 или радиус-вектором этой точки, (рис.79).
или радиус-вектором этой точки, (рис.79).
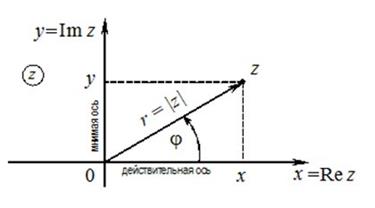 Рис. 79
Рис. 79
| 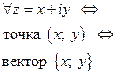
|
 Знак z во второй четверти означает, что система декартовых координат
Знак z во второй четверти означает, что система декартовых координат 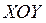 будет использоваться как комплексная плоскость. При этом ось абсцисс OX называется действительной осью, ось ординат OY называется мнимой осью.
будет использоваться как комплексная плоскость. При этом ось абсцисс OX называется действительной осью, ось ординат OY называется мнимой осью.
Дата добавления: 2015-10-19; просмотров: 875;
