С обратном каналом

Систематическими называют избыточный групповой n-значный код, каждая группа которого содержит m информационных и k=n-m контрольных символов, при этой расположение информационныхи контрольных символов в каждой группе неизменно [5].

Избыточное кодирование систематическим кодом (n,m) заключается в расчете контрольных символов для текущей m разрядной информационной группы и формирования n-разрядной группы избыточного кода. Правило вычисления контрольных символов называют правилом кодирования. На приемной стороне реализуется корректирующая способность избыточного кода: для принятой n-разрядной группы вычисляется исправляющий вектор, указывавший на номера ошибочно принятых разрядов. Исправление ошибочно принятых разрядов производится инвертированием символов этих разрядов. Правильное исправление ошибок проводится только в том случае, когда число ошибочно принятых разрядов (кратность ошибки) не превышает величины 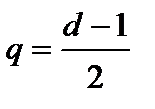, где d – кодовое расстояние избыточного n-значного кода. Правило вычисления исправляющего вектора называют правилом декодирования [6, 7].

При кодировании n-значным кодом возможно 2ⁿ различных кодовых груш (векторов). Из этого числа 2^m кодовых векторов являются разрешенными, которые и используются для передачи информации, поступающей на избыточное кодирование в виде m разрядных групп. Остальные векторы числом (2ⁿ - 2^m) не используются для передачи информации и называются запрещенными. Под правилом кодирования можно понимать правило, по которому устанавливается соответствие каждой m-разрядной информационной группе одного из 2^m разрешенных векторов n-значного избыточного кода. Под правилом декодирования можно понимать правило, по которому устанавливается соответствие каждому принятому n-значному вектору одного из разрешенных кодовых векторов.

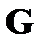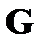Для построения избыточного кода, т.е. для определения раз­решенных n-значных кодовых векторов, а также правил кодиро­вания и декодирования, строятся производящая и проверяющая матрицы. Производящая матрица имеет порядок 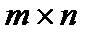, ее строками могут быть ненулевые n-значные векторы, содержащие не менее d-1 единиц, линейно независимые и отличающиеся друг от друга не менее чем в d-2 разрядах, где d – требуемое кодовое расстояние. Практически производящая матрица может быть построена дополнением единичной матрицы I порядка 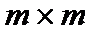к матрице 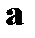порядка :

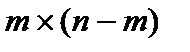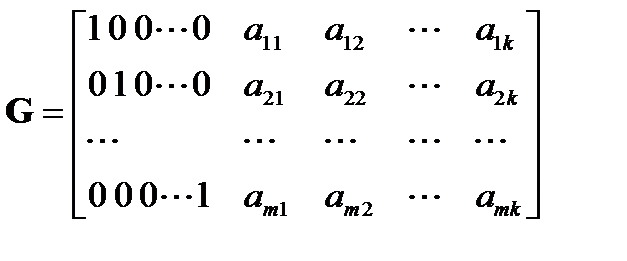(1)

Строки дополнительной матрицы 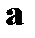должны содержать не менее d-1 единиц и различаться друг от друга не менее, чемв d-2 разрядах.

Производящая матрица определяет множество 2^m разрешенных векторов избыточного n-значного кода. Часть разрешённых векторов записана строками производящей матрицы (m векторов), остальная часть из 2^m -m-1 векторов находится в результате линейной комбинации строк производящей матрицы, т.е. суммированием по mod2 строк матриц в любых сочетаниях. Строки проверочной матрицы ортогональны строкам производящей матрицы 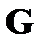. К разрешенным векторам относят также нулевой вектор.

Проверочная матрица имеет порядок 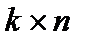и при задании производящей матрицы 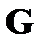в виде (1) может быть определена таким образом:

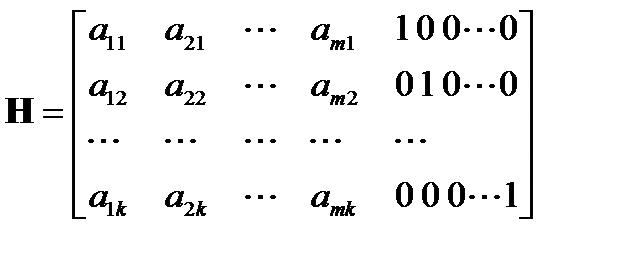(2)

Проверочная матрица линейной комбинацией строк порождает множество векторов 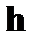, ортогональных всем разрешенным векторам кода. Как известно, условие ортогональности двух векторов 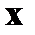и 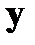выражается соотношением

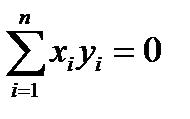, (3)

где сумма рассматривается по mod2.

Проверочная матрица необходима для вычисления исправляющего вектора 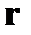, который находится в результате матричного произведения

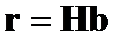(4)

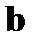проверочной матрицы на принятый вектор . Алгоритм (4) определяет правило декодирования в виде k проверок (по числу строк проверочной матрицы) на чётность:

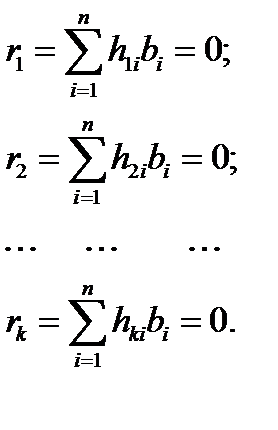(5)

В результате этих проверок вычисляются разряды исправляющего вектора 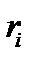. Если все проверки дают нулевую сумму (сумма по mod2), то ошибка не фиксируется. При этом либо её нет совсем, либо её кратность выходит за пределы корректирующей способности кода. И в том и в другом случае нулевые суммы 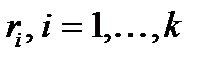являются свидетельством ортогональности принятого вектора 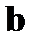векторам 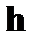, что указывает на принадлежность принятого вектора множеству разрешимых векторов. При ненулевом векторе 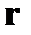фиксируется факт ошибочного приема отдельных разрядов переданного вектора. Если кратность ошибки не превышает допустимой величины, при которой возможно иcправление ошибок, то по вычисленному вектору 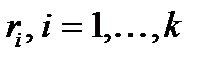можно однозначно определить номера ошибочно принятых разрядов, пользуясь заранее подготовленной таблицей соответствия. Такая таблица устанавливает соответствие каждому вектору 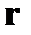определённого номера и или комбинации номеров ошибочно принятых разрядов.

В лабораторной работе изучается систематический код (7,4). Такой код имеет расстояние 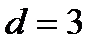и, следовательно, на приёмной стороне возможно исправление однократных ошибок. Другими словами, код обладает корректирующей способностью при условии искажения только одного разряда 7-разрядной группы.

Код (7,4) может быть построен с различными правилами кодирования и декодирования. Построим код по изложенной выше методике. Производящую матрицу 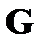запишем в виде

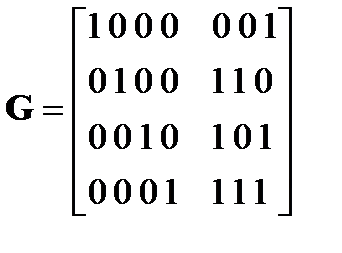(6)

Тогда проверочная матрица примет вид:

(7)

Непосредственными вычислениями нетрудно убедиться в ортогональности любой пары векторов из множеств 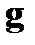и 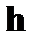, порождаемых матрицам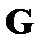и и соответственно.

Правила декодирования согласно соотношениям (4) выра­жается тремя проверками на четность:

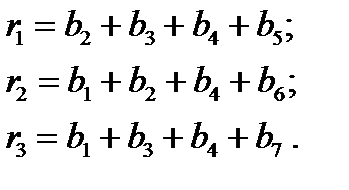(8)

В каждой проверке участвует определенная подгруппа разрядов принятого 7-значного вектора 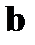. В результате проверок вычисляется исправляющий вектор 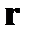. Построим таблицу соответствия каждому вектору 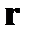номера ошибочно принятого разряда. Если ошибка произошла в разряде 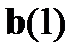и только в этом разряде, то 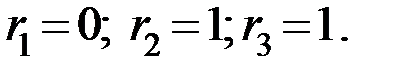При ошибочном приеме разряда 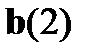значения исправляющего вектора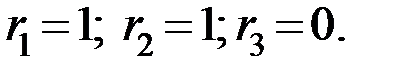

Продолжая вычисления, приходим к выводу, что искомая таблицасоответствия дается проверочной матрицей, если столбцы этой матрицы рассматривать в качестве векторов 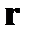. При этом номер столбца, к которому относится вычисленный вектор 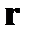и есть номер ошибочно принятого разряда.

Проверочная матрица задает и правила кодирования, т.е. правила вычисления контрольных разрядов. За контрольные разряды удобно принять такие, которые входят в каждую проверяемую подгруппу один раз. Для рассматриваемого кода (7,4) за контрольные разряды 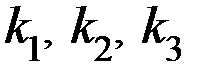следует принять последние три разряда 7-значного вектора 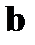: 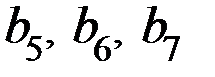, а информационную группу разрядов 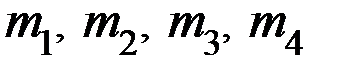разместить на позициях первых четырёх разрядов: 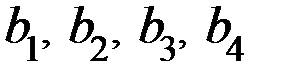. Контрольный разряд должен дополнять свою подгруппу дочетного числа единиц. Поэтому правила кодирования, записанные на основании (8) ипринятого размещении контрольных и информационных разрядов, принимают вид:

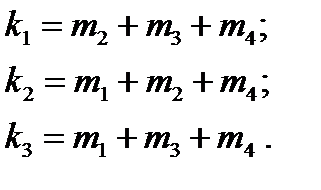(8)

Код (7,4) можно построить и так, чтобы исправляющий вектор в двоичном исчислении непосредственно давал номер ошибочного принятого разряда. Очевидно, в этом случае проверочная матрица должна иметь вид:

(9)

Код с проверочной матрицей данного вида называют кодом Хемминга [7].

Правило образования разрядов исправляющего вектора получается при записи всех разрядов 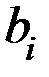в виде двоичного кода, т.е.

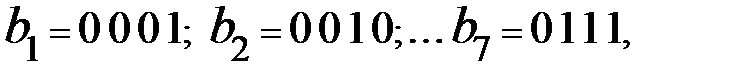
и каждая проверка есть сумма по mod2 всех разрядов, в номерах которых 1 стоит в младшем ( 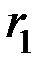), во втором ( 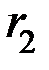) и третьем ( 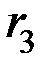) разрядах кода, т.е.

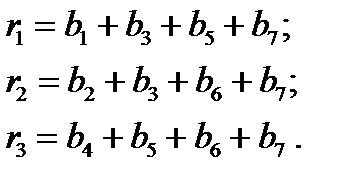(10)

Уравнения кодирования (с учетом расположения контрольных разрядов на последних позициях 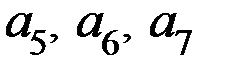7-значного кода) будут получены путем приравнивания проверочных уравнений 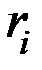нулю в виде

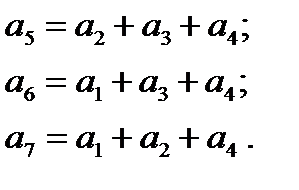(11)

Характеристики кода Хемминга приведены втаблице [7].

Таблица 1 Характеристики кода Хемминга

Число возможных ошибок	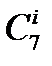Кратность ошибки
Число необнаруженных ошибок