Детектирование амплитудно-модулированных сигналов
Детектированием называется процесс выделения управляющего сигнала из модулированного. Для восстановления модулирующего процесса при обработке модулированного сигнала необходимо использовать нелинейный элемент. В частном случае детектирования амплитудно-модулированного сигнала возможно использование линейного параметрического элемента – синхронного детектора. Это следует из общего соотношения для сигнала с переменной огибающей и фазой (частотой) [1-3].
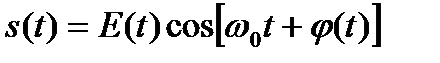 (1)
(1)
где 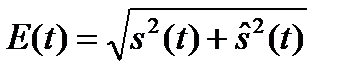 – огибающая сигнала;
– огибающая сигнала;
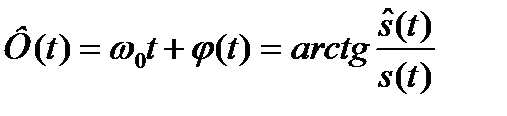 – полная фаза сигнала;
– полная фаза сигнала;
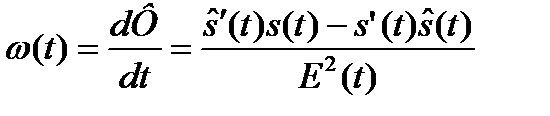 – мгновенная частота сигнала;
– мгновенная частота сигнала;
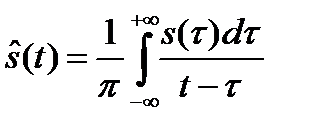 – процесс, сопряженный по Гильберту с сигналом s(t) (прямое преобразование Гильберта по отношению к сигналу s(t)),
– процесс, сопряженный по Гильберту с сигналом s(t) (прямое преобразование Гильберта по отношению к сигналу s(t)), 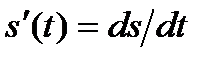 ,
, 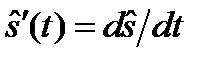 .
.
Как видно из приведенных выражений, огибающая E(t), фаза Ф(t) и частота ω(t) являются нелинейными функциями сигнала s(t), и для выделения содержащихся в них процессов необходимы нелинейные преобразования s(t).
В случае амплитудной модуляции при постоянной фазе сигнал имеет вид:
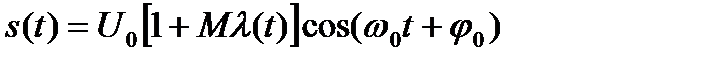 (2)
(2)
где U0 – средняя амплитуда сигнала;
λ(t) – сообщение (модулирующий процесс), нормированное таким образом, что выполняется условие 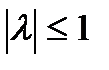 ;
;
М – коэффициент модуляции;
ω0, φ0 – соответственно, постоянные частота несущего колебания и фазовый сдвиг сигнала.
Если частота и фаза сигнала (2) известны точно, то на приемной стороне можно сформировать опорное колебание 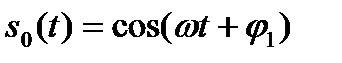 и подать его на перемножитель вместе с сигналом s(t). Тогда после умножения можно получить:
и подать его на перемножитель вместе с сигналом s(t). Тогда после умножения можно получить:
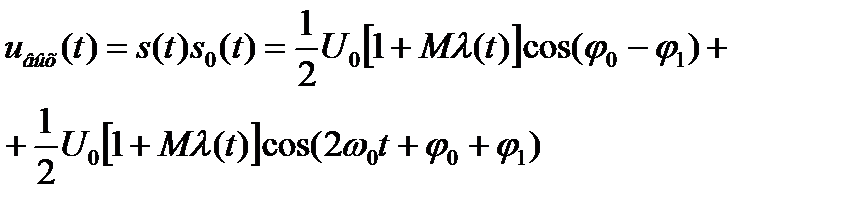 (3)
(3)
Второе слагаемое полученного напряжения uвых (t) можно устранить фильтром нижних частот без существенных искажений для сообщения λ(t), если выполняется условие ω0 >> Ωв, где Ωв – верхняя частота спектра сообщения λ(t). Вместо процесса s0(t) на перемножитель можно подать последовательность прямоугольных импульсов со скважностью, равной двум, при условии, что её период строго равен периоду несущего колебания сигнала (2), и положение фронтов импульсов совпадает с положением «нулей» колебания 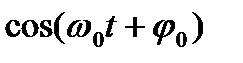 . Необходимость в фильтре нижних частот сохраняется и в этом случае.
. Необходимость в фильтре нижних частот сохраняется и в этом случае.
Сочетание перемножителя (или коммутатора при подаче на опорный вход импульсов) с фильтром нижних частот образует синхронный детектор, который является линейным элементом с переменным коэффициентом передачи (параметрическим элементом) [2, 3]. Как видно из равенства (3), для получения достаточно высокого коэффициента передачи необходимо, чтобы фазовый сдвиг опорного колебания φ1 был близок по значению к фазовому сдвигу φ0 входного AM сигнала. Поэтому основной проблемой, которую приходится решать при построении синхронного детектора, является проблема фазировки опорного и несущего колебаний. Иными словами, при создании синхронного детектора необходимо обеспечить когерентность сигнального и опорного колебаний, что означает, в первую очередь, равенство их частот и дополнительно – близость фазовых сдвигов.
Трудности создания синхронных детекторов привели к использованию для детектирования амплитудно-модулированных сигналов комбинации нелинейного элемента и фильтра нижних частот. В качестве нелинейного элемента может быть использован как транзистор, так и диод. Эффект появления низкочастотной составляющей спектра – результата нелинейного преобразования амплитудно-модулированного сигнала – можно объяснить результатом взаимодействия в нелинейном элементе (транзисторе или диоде) несущего колебания с боковыми составляющими спектра сигнала. Фильтр нижних частот выделяет низкочастотные и отсеивает высокочастотные составляющие, частоты которых близки к несущей и выше ее.
Некоторые показатели качества детектора можно оценить по характеристике детектирования [2, 3], которая представляет собой зависимость приращения постоянной составляющей тока нелинейного элемента детектора от амплитуды входного высокочастотного напряжения. Выходным параметром детекторной характеристики может служить и приращение постоянной составляющей напряжения на сопротивлении нагрузки детектора.
Рассмотрим аппроксимацию тока полупроводникового прибора как функцию подводимого напряжения в виде полинома третьего порядка. Как известно [2, 3], подобная аппроксимация обычно применяется при относительно небольших амплитудах переменных напряжений:
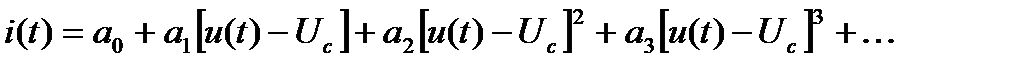 (4)
(4)
где 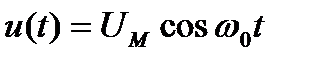 – переменное входное напряжение с амплитудой UM и частотой ω0;
– переменное входное напряжение с амплитудой UM и частотой ω0;
Uc – постоянное напряжение смещения.
Выделяя постоянную составляющую в составе тока, описываемого равенством (4), можно получить:
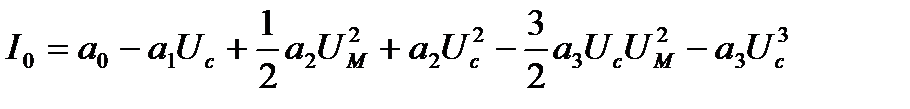 (5)
(5)
Выделяя в полученном выражении слагаемые, зависящие от амплитуды сигнала UM, получаем выражение для характеристики детектирования:
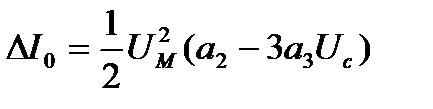 (6)
(6)
Как видно из полученного выражения, характеристика является квадратичной функцией амплитуды подводимого напряжения.
При амплитудной модуляции обычно зависимость амплитуды от сообщения является линейной функцией:
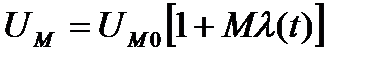 (7)
(7)
где UM0 – среднее значение амплитуды;
М – коэффициент модуляции.
λ(t) – сообщение, нормированное к единице |λ|макс=1.
Можно убедиться, что при использовании детектора с характеристикой (6), процесс на выходе получает нелинейные искажения:
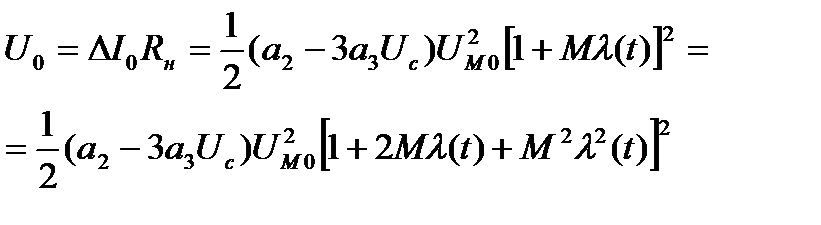 (8)
(8)
где Uд – напряжение на выходе детектора;
Rн – сопротивление нагрузки детектора.
Предполагается, что изменение напряжения на выходе детектора не изменяет тока электронного прибора, на котором выполнен детектор.
В полученном выражении (8) нелинейные искажения сообщения λ(t) представлены последним слагаемым. Полагая 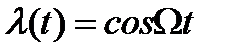 , можно оценить коэффициент нелинейных искажений Кν как отношение амплитуды второй гармоники косинусоидального закона изменения сообщения к амплитуде его первой гармоники.
, можно оценить коэффициент нелинейных искажений Кν как отношение амплитуды второй гармоники косинусоидального закона изменения сообщения к амплитуде его первой гармоники.
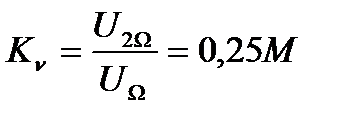 (9)
(9)
где 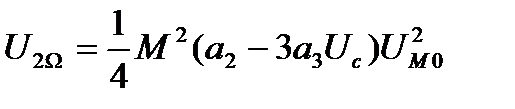 – амплитуда второй гармоники сообщения;
– амплитуда второй гармоники сообщения;
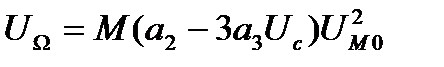 – амплитуда первой гармоники сообщения λ(t).
– амплитуда первой гармоники сообщения λ(t).
Из выражения (9) следует, что коэффициент нелинейных искажений пропорционален коэффициенту модуляции, и при квадратичной характеристике детектирования глубина модуляции должна быть невысокой, если нелинейные искажения важны.
Для получения характеристики детектирования, близкой к линейной, используются сигналы с большой средней амплитудой. При этом справедлива кусочно-линейная аппроксимация вольтамперной характеристики электронного прибора, на котором выполняется детектирование – сток-затворной при использовании полевого транзистора или зависимости тока диода от напряжения на нём в случае диодного детектора.
Рассмотрим диодный детектор, вольтамперная характеристика которого при большой амплитуде входного сигнала может быть аппроксимирована линейно-ломаной зависимостью:
| Su, при u > 0 i = 0, при u < 0 |
(10)
где S – крутизна характеристики.
| UM |
| Д |
| CH |
| UД |
| RH |
Рисунок 1 – Принципиальная схема последовательного
диодного детектора
Для постоянной составляющей тока диода можно записать выражение:
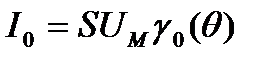 (11)
(11)
где 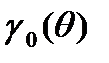 – коэффициент разложения косинусоидального импульса для постоянной составляющей:
– коэффициент разложения косинусоидального импульса для постоянной составляющей:
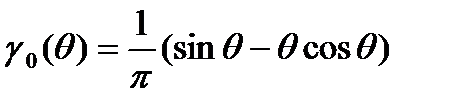 (12)
(12)
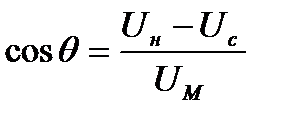 (13)
(13)
θ – угол отсечки импульса тока;
Uн – параметр кусочно-линейной аппроксимации характеристики, равный значению напряжения, начиная с которого характеристика становится линейно растущей (при S > 0), для диода можно полагать Uн = 0;
Uс – напряжение смещения рабочей точки относительно u = 0.
Учитывая, что в диодном детекторе напряжение на нагрузке приложено навстречу движения тока, можно полагать Uc = -Uд, где Uд – напряжение на выходе детектора, равное:
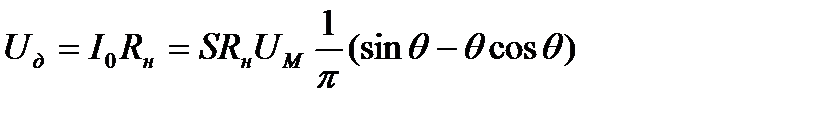 (14)
(14)
где Rн – сопротивление нагрузки детектора. Таким образом
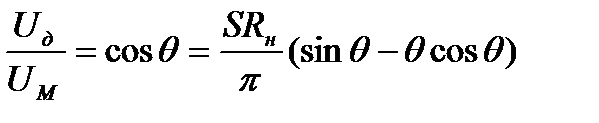 (15)
(15)
Уравнение (15) позволяет найти угол отсечки θ, а cos(θ) можно назвать коэффициентом передачи детектора. При достаточно большом значении сопротивления нагрузки, когда выполняется неравенство S Rн >> 1, угол θ является небольшим и величина cos(θ) близка к единице. Разделив левую и правую части равенства (15) на cos(θ), разлагая tg(θ) в ряд Тейлора и ограничиваясь двумя членами разложения 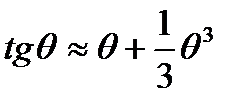 , можно получить приближенное равенство:
, можно получить приближенное равенство:
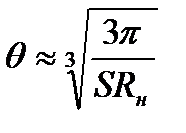 (16)
(16)
Тогда характеристика детектирования может быть описана зависимостью
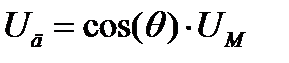 (17)
(17)
и представляет собой прямую, исходящую из начала координат с наклоном, практически равным единице.
В реальных случаях начало характеристики детектирования имеет квадратичный характер из-за малых амплитуд входного сигнала и с ростом UМ парабола постепенно переходит в линейную зависимость (17).
Процессы, происходящие в истоковом детекторе, выполненном на полевом транзисторе, при больших амплитудах входного сигнала подобны процессам, описанным выше, в «линейном» диодном детекторе.
Упрощённая принципиальная электрическая схема истокового детектора приведена на рисунке 2.
| – + Uсм |
| VT |
| + – Ec |
| UM |
| CH |
| RH |
| UД |
Рисунок 2 – Упрощенная принципиальная схема истокового детектора на
полевом транзисторе с «левой» характеристикой
Для получения линейной детекторной характеристики напряжение смещения в истоковом (как и в стоковом) детекторе подбирается равным начальному напряжению Uн. В общем случае угол отсечки θ в истоковом детекторе определяется выражением
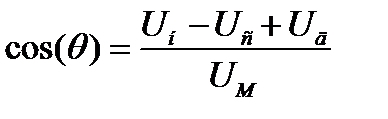 (18)
(18)
Учитывая указанное выше условие Uн = Uс, можно получить выражение 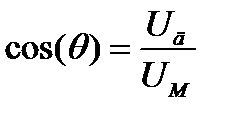 , аналогичное подобному выражению в диодном детекторе. Поэтому детекторная характеристика истокового детектора при больших значениях амплитуды входного сигнала также является линейной.
, аналогичное подобному выражению в диодном детекторе. Поэтому детекторная характеристика истокового детектора при больших значениях амплитуды входного сигнала также является линейной.
Для обеспечения качества выделения огибающей входного сигнала важное значение имеет выбор ёмкости нагрузки детектора. Постоянная времени нагрузки детектора должна быть намного выше периода несущей частоты сигнала и ниже периода высшей частоты спектра огибающей входного сигнала:
2π/ω0 << RнCн < 2π/Ωв (19)
Первое условие необходимо для хорошей фильтрации напряжения несущей частоты, а второе называется условием безынерционности детектора для огибающей и служит для устранения искажений огибающей, которые возможны, если при уменьшении амплитуды напряжения на входе детектора ёмкость нагрузки не успеет разрядиться и напряжение на ней «запрёт» диод.
Дата добавления: 2015-10-19; просмотров: 2242;
