В цепь затвора транзистора VТ поступает сумма трёх напряжений

u_з(t) = u(t) + u_м(t) + U_см (3)

где u(t) – высокочастотное гармоническое напряжение несущей частоты;

u_м(t) – низкочастотный модулирующий процесс;

U_см – постоянное напряжение смещения.

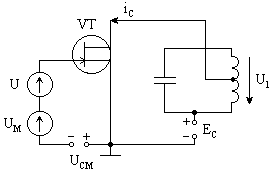
Рисунок 2 – Упрощенная принципиальная схема модулятора смещением на полевом транзисторе

Нагрузкой транзисторного усилителя является колебательный контур, выделяющий, как указывалось выше, модулированный по амплитуде сигнал u₁(t). Таким образом, модулятор, представленный на схеме, является нелинейным резонансным усилителем, усиление которого управляется модулирующим процессом u_м(t). Качество модуляции можно оценить по виду модуляционной характеристики.

В практике построения и исследования модуляторов различают два вида модуляционных характеристик [2, 3]. Зависимость амплитуды первой гармоники тока усилителя или амплитуды напряжения на нагрузке от напряжения смещения называется статической модуляционной характеристикой. При этом полагается u_м=0 – учитывается, что изменение смещения осуществляется изменением модулирующего процесса. Вторым видом модуляционной характеристики является динамическая, представляющая собой зависимость коэффициента амплитудной модуляции сигнала, выделяемого на нагрузке модулятора, от амплитуды модулирующего (чаще всего гармонического с низкой частотой Ω) напряжения u_м(t). Меняя амплитуду высокочастотного напряжения u(t), можно получить семейство модуляционных характеристик как статических, так и динамических.

При теоретическом расчёте характеристик необходима аппроксимация проходной характеристики транзистора. Известно [2, 3], что при небольших значениях действующих напряжений целесообразна полиномиальная характеристика. Используя аппроксимацию зависимости тока стока от напряжения на затворе полиномом третьего порядка, можно получить:

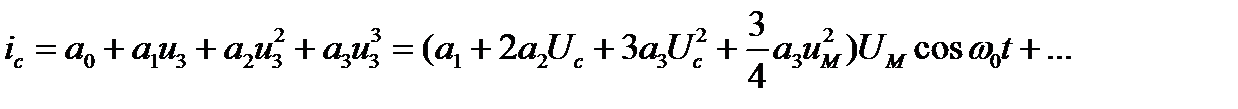(4)

где a₀, a₁, a₂, a₃ – коэффициенты полинома, аппроксимирующего характеристику транзистора.

В равенстве (4) показаны только слагаемые, образующие гармоническое колебание тока с частотой ω₀, при этом учтено, что соs³ω₀t=(3соsω₀t + соs(3ω₀t)) /4 .

Как видно из (4), статическая модуляционная характеристика выражается формулой:

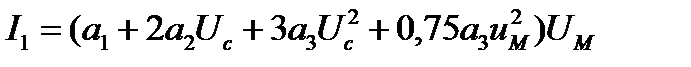(5)

И является квадратичной функцией смещения U_c. Отклонение характеристики от линейности при использованной аппроксимации вызывается наличием кубического члена, при его отсутствии модуляционная характеристика линейна. Таким образом, чем ближе характеристика транзистора к квадратичной функции (отрезку параболы), тем более линейной является статическая модуляционная характеристика.

При линейно-ломаной аппроксимации уравнение сток-затворной характеристики транзистора имеет вид (рисунок 3), где S – крутизна наклонного участка аппроксимирующей функции.

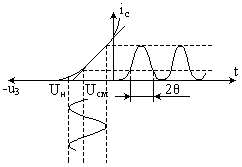
Рисунок 3 – Графики, поясняющие режим транзистора

При u_вх(t) = U + U_мcosω₀t закон изменения тока стока имеет форму, близкую к периодической последовательности «отсеченных» косинусоидальных импульсов. Угол отсечки θ определяется выражением [2, 3]

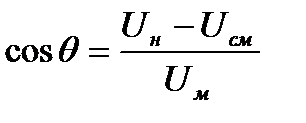(6)

которое справедливо при условии 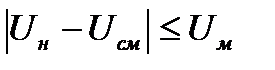. В противоположном случае «отсечка» отсутствует.

Разлагая периодическую функцию, описывающую закон изменения тока, в ряд Фурье, для амплитуды первой гармоники можно получить [2, 3]

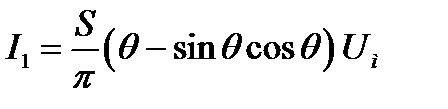. (7)

Изменяя значение напряжения смещения от минимального u_{см мин}=U_н – U_м до максимального u_{см макс}= U_н – U_м, вычисляя для каждого значения u_см угол отсечки θ и подставляя его в равенство (8), можно построить статическую модуляционную характеристику и для данного способа аппроксимации.

Расчёт и построение динамической модуляционной характеристики можно выполнить, задаваясь минимальным и максимальным значением смещения и находя минимальные и максимальные значения амплитуд первой гармоники тока стока I_1мин и I_1макс. Тогда значение коэффициента модуляции тока может быть найдено из равенства

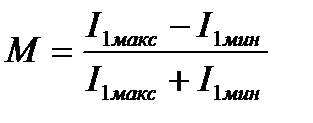(8)

При экспериментальном измерении коэффициента модуляции вместо амплитуд первых гармоник тока используются амплитуды напряжения на нагрузке усилителя – параллельном колебательном контуре.

3. Характеристика лабораторной установки:

Лабораторная работа № 2 выполняется с использованием виртуальной модели (рисунок 4) лабораторного стенда, имеющего название «Нелинейные цепи».

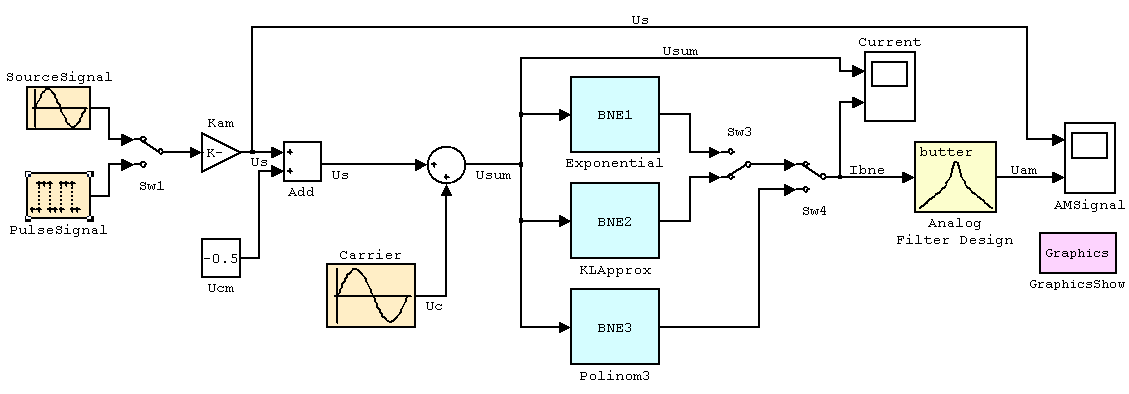
Рисунок 4 – Блок-схема для исследования виртуального АМ-модулятора

В составе блок-схемы три модели безынерционного нелинейного элемента BNE (входная характеристика полевого транзистора КП-307 изображена на рисунке 5): BNE1 – экспоненциальная Exponential, BNE2 – кусочно-линейная KLApprox и BNE3 – степенная третьего порядка Polinom3.

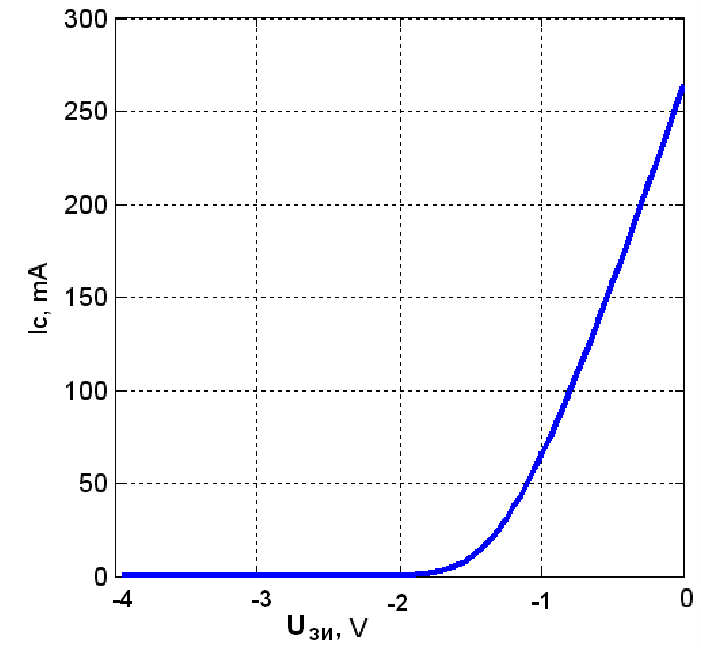
Рисунок 5 – Входная характеристика полевого транзистора КП-307

Колебательный контур представляется полосовым фильтром, настроенным на частоту несущей (блок Carrier). На вход модели транзистора могут подаваться три вида напряжений: последовательность прямоугольных импульсов с блока PulseSignal, гармоническое напряжение с блока SourceSignal и постоянное напряжение с блока Uc. Первые два блока моделируют низкочастотные модулирующие сигналы, а третий блок – отрицательное напряжение смещения на затворе транзистора.

Напряжение на контуре наблюдается на осциллографе AMSignal, на нём же проводятся измерения высокочастотного напряжения. Необходимые подключения генераторов, напряжения смещения, напряжения питания на сток транзистора осуществляются специальными перемычками.