Исследование функций взаимной корреляции случайных процессов и их производных

Функцией взаимной корреляции случайных процессов X(t) и Y(t) называется смешанный центральный момент второго порядка системы двух сечений Х(t₁), Y(t₂), рассматриваемый как функция моментов времени t₁ и t₂:

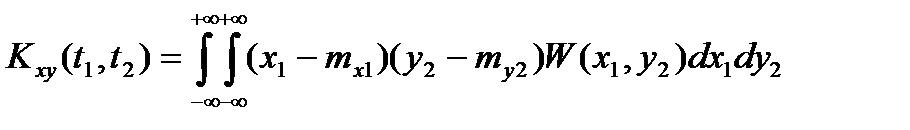(1)

где W(x₁,y₂) – плотность вероятности системы случайных величин X₁ и Y₂;

x₁, y₂ – значения сечений X(t₁) и Y(t₂) соответственно;

m_x1, m_y2 – математические ожидания сечений X(t₁) и Y(t₂).

В случае стационарных и стационарно связанных случайных процессов X(t) и Y(t) функция взаимной корреляции не зависит от значений моментов времени t₁ и t₂, а зависит от их разности τ = t₁ - t₂.

Функция взаимной корреляции К_ху(τ) характеризует линейную статистическую связь стационарных и стационарно связанных случайных процессов X(t) и Y(t) в зависимости от их временного сдвига относительно друг друга. В точках, где значения функции взаимной корреляции К_ху(τ) равны нулю линейная зависимость Y(t) от X(t) и наоборот отсутствует.

Рассмотрим основные свойства функции взаимной корреляции 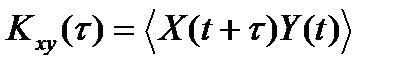. Здесь угловые скобки означают вычисление математического ожидания. Предполагается также, что процессы X(t) и Y(t) имеют нулевые математические ожидания. При выборе индексов обозначения функции К_ху(τ) на первое место условно ставится опережающий процесс. Отсюда следует:

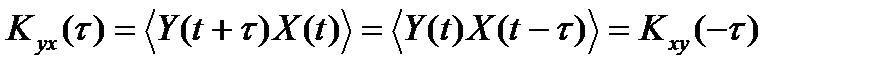(2)

Таким образом перемена порядка следования индексов эквивалентна изменению знака переменной τ.

В общем случае функция корреляции К_ху(τ) не является ни четной, ни нечетной функцией. Поэтому взаимная спектральная плотность мощности процессов X(t) и Y(t) в общем случае является комплексной функцией.

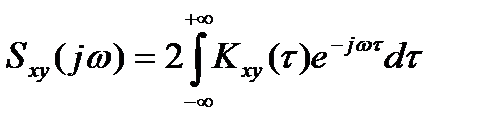(3)

Рассмотрим ряд конкретных функций взаимной корреляции.

В качестве первого примера найдем функцию взаимной корреляции между процессами на выходе и на входе линейной цепи. Выражение, связывающее выходной и входной процессы в указанном выше случае имеет вид:

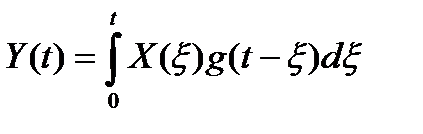(4)

где g(t) – импульсная реакция цепи.

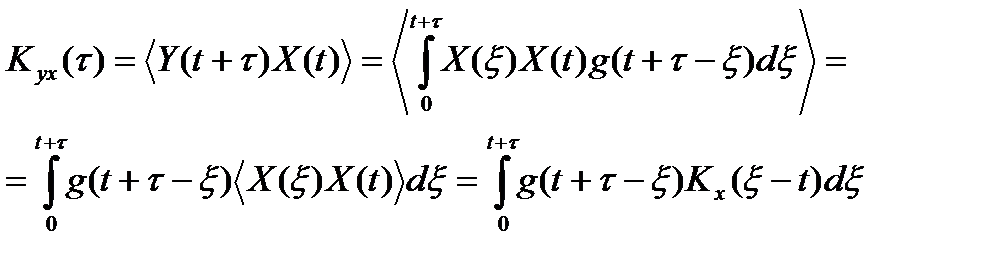(5)

Полученное выражение справедливо как для переходного, так и для стационарного режима. В стационарном режиме пределы интегрирования могут быть бесконечными, а функция корреляции не зависит от времени. Тогда:

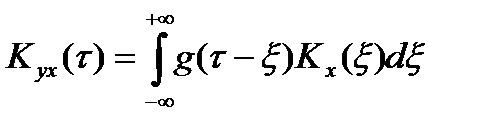(6)

где К_х(τ) – функция автокорреляции входного процесса Х(t).

Таким образом, функция взаимной корреляции стационарных процессов на выходе и входе линейной цепи равна свертке функции корреляции входного процесса и импульсной реакции цепи.

Применяя к левой и правой части (6) преобразование Фурье в форме, представленной равенством (3), можно получить:

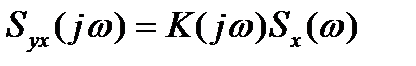(7)

где S_yx(jω) – взаимная спектральная плотность мощности процессов Y(t) и X(t);

K(jω) – коэффициент передачи цепи;

S_x(ω) – спектральная плотность мощности процесса X(t).

Взаимная спектральная плотность мощности входного X(t) и выходного Y(t) процесса может быть получена обращением по Фурье взаимной функции корреляции K_xy(τ), которая связана с K_yx(τ) равенством (2).

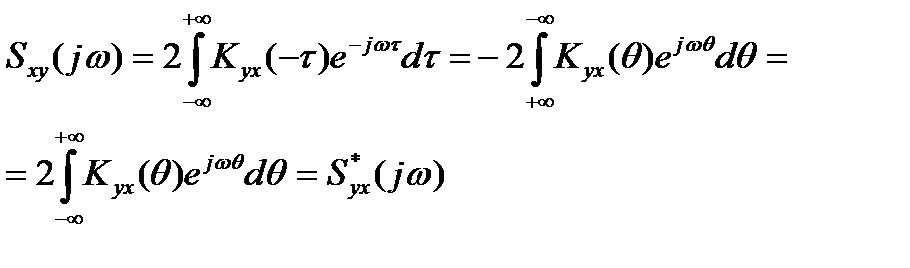(8)

где проведена замена переменной интегрирования τ на –θ.

Используя полученное выражение и равенство (7), можно получить выражение для взаимной спектральной плотности процессов на входе и выходе линейной цепи:

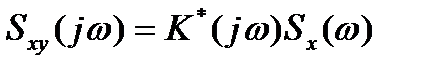(9)

Полученные результаты можно использовать для исследования функции взаимной корреляции случайного процесса и его производной по времени.

Как известно из теории цепей, коэффициент передачи дифференцирующей цепи, процесс на выходе которой равен производной входного процесса, можно представить выражением:

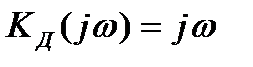(10)

В этом случае функция взаимной корреляции производной случайного процесса 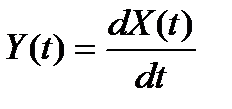и исходного процесса X(t) может быть записана в виде:

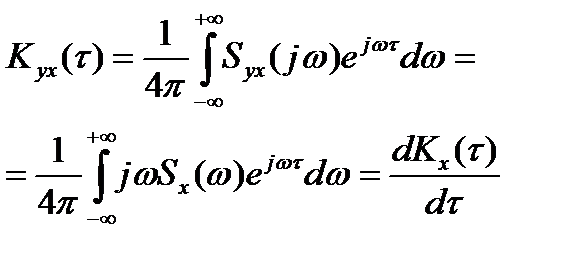(11)

Таким образом, функция взаимной корреляции между производной и случайным процессом равна производной функции корреляции случайного процесса.

Отметим основные свойства функции взаимной корреляции 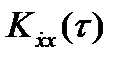, где 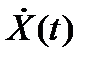– производная процесса X(t).

1. Известно, что функция корреляции K_x(τ) стационарного случайного процесса является чётной функцией τ и в точке τ=0 имеет максимум, равный дисперсии. Следовательно, функция взаимной корреляции 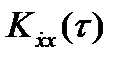является нечетной функцией и 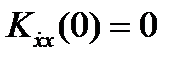, то есть в одинаковые моменты времени стационарный процесс и его производная не коррелированны, а в случае нормального распределения X(t) и независимы.

2. Если функция корреляции K_x(τ) недифференцируемая, то случайный процесс X(t) считается недифференцируемым.

3. В связи с тем, что функция K_x(τ) в начале координат максимальна, то ее производная при τ = 0 равна нулю. Поэтому при монотонном характере функции корреляции K_x(τ) при τ > 0 ее производная отрицательна, а при τ < 0 положительна. В силу того, что функция корреляции K_x(τ) является четной, то функция 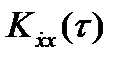не четна. При увеличении абсолютного значения τ функция взаимной корреляции 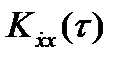стремится к нулю.

Рассмотрим функции взаимной корреляции случайных процессов на выходах цепей б) и в) лабораторной работы № 4 (см. рисунок 2 работы № 4) и их производных. Принципиальные схемы цепей б) и в) представлены на рисунке 1.

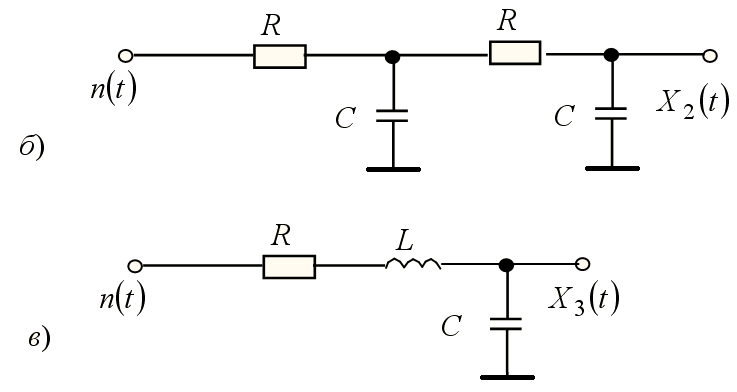
Рисунок 1 – Принципиальные схемы цепей, формирующих

случайные процессы X₂(t) и X₃(t)

Резистор R в цепи в) может быть замкнут специальным проводником.

Нормированные корреляции процессов X₁(t) и X₃(t) имеют вид:

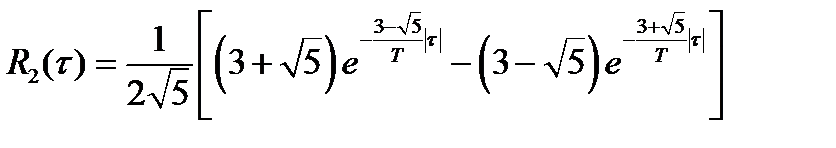(12)

где T=RC;

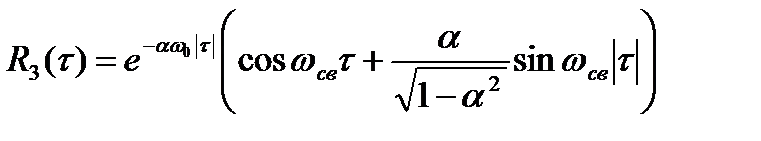(13)

где , , ,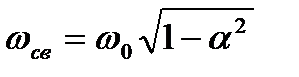

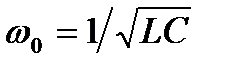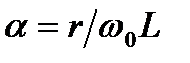r – сопротивление потерь в катушке индуктивности цепи в).

Равенство (13) получено в предположении, что резистор R замкнут (на схеме рисунка 1,в отсутствует).

Аналогично, функция взаимной корреляции случайного процесса X₂(t) и его производной по времени 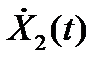равна:

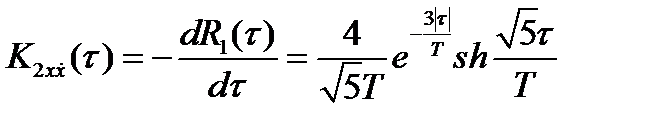(14)

где 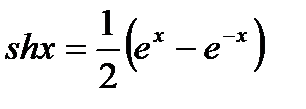– функция гиперболического синуса.

Функция взаимной корреляции процесса X₃(t) и его производной по времени 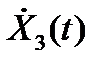может быть представлена в виде:

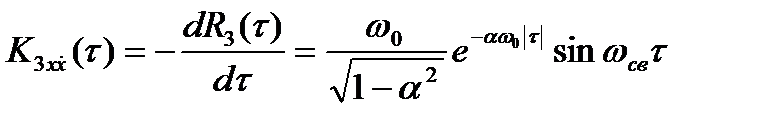(15)

Как видно из приведенных выражений, обе функции взаимной корреляции нечетны, поэтому при экспериментальных исследованиях достаточно снять их зависимость от сдвига τ либо при положительных, либо при отрицательных его значениях.

3. Характеристика лабораторной установки:

Лабораторная работа выполняется на блоке № 2 «Спектры и корреляционные функции». Упрощённая функциональная схема выполнения лабораторной работы представлена на рисунке 2.

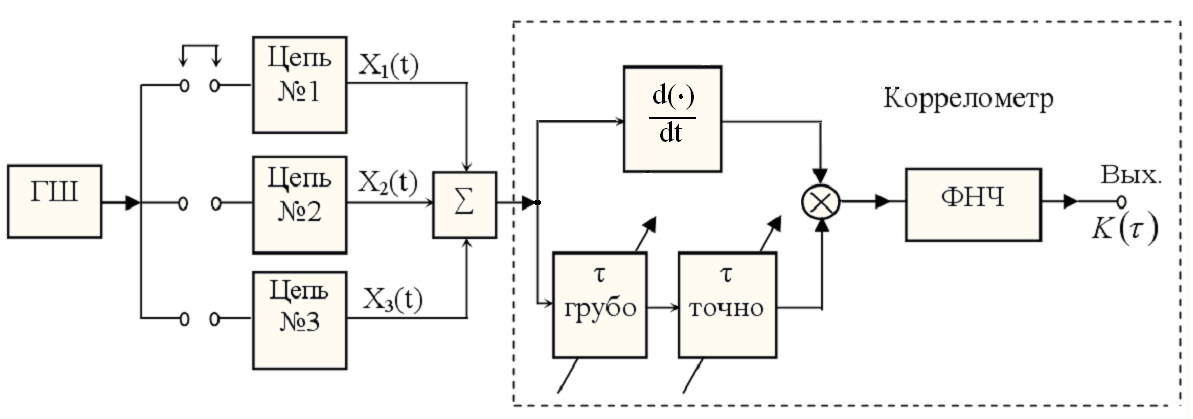
Рисунок 3 – Упрощенная функциональная схема выполнения

лабораторной работы № 5

Генератор шума (ГШ) формирует случайный широкополосный процесс, математической моделью которого является белый шум – случайный процесс с постоянной, независящей от частоты спектральной плотностью мощности. Подключая с помощью перемычек исследуемые цепи, можно сформировать процессы X₁(t), X₂(t) и X₃(t), описанные в методических указаниях к лабораторной работе № 4. Эти процессы поступают на дифференцирующий операционный усилитель, выходные процессы которого совместно с исходными процессами подаются на коррелятор, состоящий из устройства управляемой переменной задержки, перемножителя и фильтра нижних частот ФНЧ, выполняющего операцию нахождения среднего значения произведения двух перемножаемых процессов:

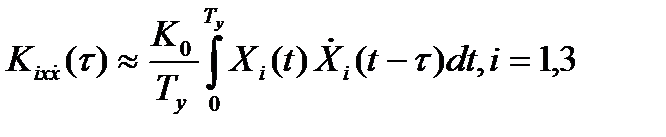(16)

Здесь К₀ – постоянный коэффициент, учитывающий коэффициенты передачи дифференцирующего операционного усилителя и перемножителя; T_y – время усреднения, в первом приближении равно постоянной времени ФНЧ коррелометра. Управление временем задержки переключателями.

В связи с наличием на выходе схемы перемножения постоянной составляющей, не зависящей от произведения входных процессов, при построении графиков функций взаимной корреляции необходимо из напряжения на выходе u_к(τ_з), соответствующего времени задержки τ_з, вычесть показания вольтметра, полученные при нулевой задержке, то есть строить функцию взаимной корреляции по формуле:

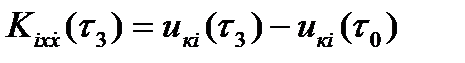(17)

где u_кi(τ_з) – показания вольтметра (или осциллографа) при измерении значения функции взаимной корреляции случайного процесса X_i(t) и его производной по времени 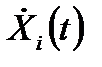при τ = τ_з.

Структурная схема Simulink-модели, соответствующая реальной установке, изображённой на рисунке 3, приведена на рисунке 4. Здесь гауссов белый шум с генератора Gaussian Noise Generator или равномерный белый шум с генератора Uniform Noise Generator сразу подаётся на входы всех трёх исследуемых цепей, а к коррелометру (блок XY-Correlometer) выходы цепей подключаются с помощью переноса точек подсоединения. Отличие коррелометра в настоящей работе от коррелометра в предыдущей состоит в том, что блок XY-Correlometer имеет два входа, на которые можно подавать как один и тот же сигнал (это определение АКФ), или различные сигналы (это определение ВКФ). Время задержки 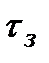задаётся как единственный параметр коррелометра и меняется от 0 до 10*RC мкс. Поскольку постоянная времени, как и ранее, принята равной одной секунде (RC = 1 с), то в модели максимальная задержка 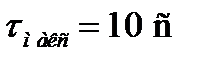практически для всех цепей лежит за пределами времени корреляции каждого из процессов.

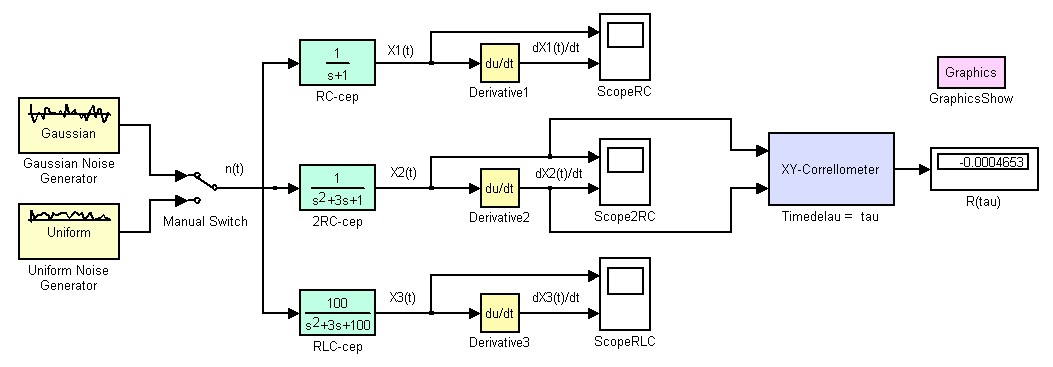
Рисунок 4 – Блок-схема модели для исследования статистических

характеристик случайных процессов и их производных

Индикация результатов моделирования проводится следующим образом. Во-первых, выходные сигналы и их производные от каждой цепи можно наблюдать на осциллографах ScopeRC, Scope2RC и ScopeRLC соответственно. Во-вторых, все эти шесть процессов передаются в рабочее пространство системы MATLAB, где в дальнейшем их цифровые модели обрабатываются и зарисовываются с помощью М-функции LabRabRCS5Obr. В-третьих, к выходу блока коррелометра подключён цифровой дисплей, на котором в конце времени моделирования T можно получить числовую оценку уровня корреляции R_x(tau) ≈ R_x(T, tau).