Восстановление аналоговых сигналов

Все устройства, предназначенные для демодуляции сигналов, будут рассмотрены при изучении конкретных систем передачи и аппаратуры, входящей в состав этих систем.При приеме сигналов ИКМ для восстановления аналогового сигнала необходимо преобразовать цифровой сигнал (последовательность двоичных импульсов) в квантованный АИМ сигнал (та­кое преобразование называется декодированием) и затем осуществить операцию демодуляции, т.е. выделения из АИМ-сигнала аналогового сигнала s(t).Итак, при использовании ИКМ выполняются следующие преобразования аналогового сигнала: в пункте передачи – амплитудно-импульсная модуляция, квантование и кодирование; в пунк­те приема – декодирование и демодуляция квантованного АИМ сигнала. Полученный на приеме аналоговый сигнал отличается от переданного, так как образуется из квантованных импуль­сов, амплитуды которых равны не мгновенным значениям сигнала s(t), а ближайшим разрешенным значениям.Таким образом, операция квантования вносит в процесс передачи сигнала неустранимую ошибку, которая тем меньше, чем больше уровней квантования.А как узнать, какое десятичное число скрывается под его записью в двоичной системе? Правило простое: под каждым разрядом двоичного числа следует записать его «вес». Те «веса», которые соответствуют единичным разрядам, нужно сложить. Полученная сумма и явится десятичным числом. Вот перед нами число 1001011, записанное в двоичной нумерации. Поступаем согласно сказанному выше:

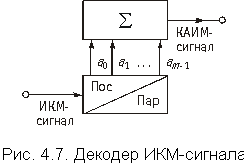
Как видим, заинтересовавшее нас число складывается из единицы, двойки, восьмерки и шестидесяти четырех (1 + 2 + 8 + 64). Очевидно, оно равно 75. Попробуйте самостоятельно определить, какому числу соот­вет­ствует его двоичная запись 10110011.В состав декодера входит пре­образователь последовательного кода в параллельный (рис. 4.7), на выходах которого появляется набор единиц и нулей, соответствующий принятой кодовой комбинации. Каждая единица (токовый импульс) поступает на вход сумматора с весом, где увеличивается в 2^k раз. На выходе сумматора возникает импульс, амплитуда которого определяется кодовой комбинацией на входе декодера.Например, при прохождении кодовой комбинации 0100110 на первый, четвертый, пятый и седьмой входы сумматора напряжение не подается (бестоковые импульсы), а на второй, третий и шестой входы подается напряжение, которое увеличивается соответственно в 2¹, 2² и 2⁵ раз. На выходе сумматора появляется напряжение, пропорциональное 2¹ + 2² + 2⁵ = 38, т.е. квантованный АИМ-сигнал.На следующем шаге необходимо из отсчетных значений тока получить непрерывный ток. Сделать это нам поможет обычный конденсатор небольшой емкости, который при кратковременном воздействии на него тока (т.е. отсчетного значения) мгновенно зарядится и будет удерживать заряд до следующего кратковременного воздействия. Отметим еще раз, что восстановленная таким путем кривая непрерывного тока будет несколько отличаться от той, которая была получена на клеммах микрофона: она будет иметь плоские ступеньки между отсчетными значениями. Можно сказать, что процесс взятия отсчетных значений и последующего восстановления непрерывной кривой тока микрофона сопровождается специфическими искажениями, которые могут повлиять на качество воспроизведения звука. Однако на практике для восстановления тока используют не конденсатор, а более сложные схемы, делающие форму восстановленного тока похожей на форму исходного тока и тем самым сводящие на нет действия указанных искажений.

Контрольные вопросы

1. Что такое цифровой сигнал?
2. С какой частотой следует дискретизировать аналоговый сигнал?
3. Как определить ошибку квантования сигнала?
4. В чем заключается принцип двоичного кодирования сигнала?
5. Как восстановить аналоговый сигнал из цифрового?

Список литературы
1. Крук Б.И., Попов Г.Н. ... И мир загадочный за занавесом цифр: Цифровая связь. – 2-е изд., испр. – Новосибирск: ЦЭРИС, 2001. – 264 с.
2. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова. – М.: Радио и связь, 2000. – 592 с.
3. Журавлева О.Б., Крук Б.И. Дискретные сигналы и цепи: 26 вопросов и ответов: Учебное пособие для дистанционного обучения. – Новосибирск: СибГУТИ, 1999. – 100 с.