Показатели надежности технических систем

Показателями надежности называют количественные характеристики одного или нескольких свойств объекта, составляющих его надежность. К таким характеристикам относят, например, временные понятия – наработку, наработку до отказа, наработку между отказами, ресурс, срок службы, время восстановления. Значения этих показателей получают по результатам испытаний или эксплуатации.

По восстанавливаемости изделий показатели надежности подразделяют на показатели для восстанавливаемых изделий и показатели невосстанавливаемых изделий.

Применяются также комплексные показатели. Надежность изделий, в зависимости от их назначения, можно оценивать, используя либо часть показателей надежности, либо все показатели.

Показатели безотказности:

– вероятность безотказной работы –вероятность того, что в пределах заданной наработки отказ объекта не возникает;

– средняя наработка до отказа –математическое ожидание наработки объекта до первого отказа;

– средняя наработка на отказ –отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки;

– интенсивность отказов –условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Этот показатель относится к невосстанавливаемым изделиям.

Показатели долговечности.

Количественные показатели долговечности восстанавливаемых изделий делятся на 2 группы.

1. Показатели, связанные со сроком службы изделия:

– срок службы –календарная продолжительность эксплуатации от начала эксплуатации объекта или ее возобновление после ремонта до перехода в предельное состояние;

– средний срок службы –математическое ожидание срока службы;

– срок службы до первого капитального ремонта агрегата или узла – это продолжительность эксплуатации до ремонта, выполняемого для восстановления исправности и полного или близкого к полному восстановления ресурса изделия с заменой или восстановлением любых его частей, включая базовые;

– срок службы между капитальными ремонтами, зависящий преимущественно от качества ремонта, т. е. от того, в какой степени восстановлен их ресурс;

– суммарный срок службы – это календарная продолжительность работы технической системы от начала эксплуатации до выбраковки с учетом времени работы после ремонта;

– гамма-процентный срок службы –календарная продолжительность эксплуатации, в течение которой объект не достигнет предельного состояния с вероятностью γ, выраженной в процентах.

Показатели долговечности, выраженные в календарном времени работы, позволяют непосредственно использовать их в планировании сроков организации ремонтов, поставки запасных частей, сроков замены оборудования. Недостаток этих показателей заключается в том, что они не позволяют учитывать интенсивность использования оборудования.

2. Показатели, связанные с ресурсом изделия:

– ресурс –суммарная наработка объекта от начала его эксплуатации или ее возобновление после ремонта до перехода в предельное состояние.

– средний ресурс –математическое ожидание ресурса; для технических систем в качестве критерия долговечности используют технический ресурс;

– назначенный ресурс – суммарная наработка, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния;

– гамма-процентный ресурс –суммарная наработка, в течение которой объект не достигнет предельного состояния с заданной вероятностью γ, выраженной в процентах.

Единицы для измерения ресурса выбирают применительно к каждой отрасли и к каждому классу машин, агрегатов и конструкций отдельно. В качестве меры продолжительности эксплуатации может быть выбран любой неубывающий параметр, характеризующий продолжительность эксплуатации объекта (для самолетов и авиационных двигателей естественной мерой ресурса служит налет в часах, для автомобилей – пробег в километрах, для прокатных станов – масса прокатанного металл в тоннах). Если наработку измерять числом производственных циклов, то ресурс будет принимать дискретные значения.

Понятие ресурс можно характеризовать как чистое время работы объекта без учета остановок.

Принято различать: ресурс до первого ремонта, межремонтный ресурс, назначенный ресурс, гамма-процентный ресурс, средний ресурс.

Назначенный ресурс – суммарная эксплуатация объекта должна быть прекращена независимо от его технического состояния.

Остаточный ресурс – суммарная наработка объекта от момента контроля его технического состояния до перехода в предельное состояние.

Назначенный срок службы – календарная продолжительность эксплуатации, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния.

Назначенный срок хранения – календарная продолжительность хранения, при достижении которой хранение объекта должно быть прекращено независимо от его технического состояния.

Цель установления этих показателей заключается в обеспечении принудительного, заблаговременного прекращения применения объекта по назначению, исходя из требований безопасности, технико-экономических соображений.

При достижении объектом назначенного ресурса (назначенного срока службы, назначенного срока хранения) в зависимости от назначения объекта, особенности эксплуатации, технического состояния и других факторов объект может быть списан, направлен в ремонт, передан для применения не по назначению, переконсервирован (при хранении) или может быть принято решение о продолжении эксплуатации.

Назначенный ресурс может выражаться различными величинами: часами работы (например, для двигателей), количеством выстрелов (для орудий), километрами пробега и т. д.

Назначение ресурса обязательно для авиационной, военной, космической техники. В настоящее время это понятие все шире применяется во всех отраслях промышленности в виде гарантированного ресурса, который изготовитель гарантирует потребителю.

Гамма-процентный ресурс – суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью g, выраженный в процентах.

Средний ресурс – математическое ожидание ресурса.

Гамма-процентный срок службы – календарная продолжительность эксплуатации, в течение которой объект не достигает предельного состояния с вероятностью g, выраженной в процентах.

Средний срок службы – математическое ожидание срока службы.

Показатели долговечности отсчитывают от ввода в эксплуатацию до окончательного снятия с эксплуатации.

Эти показатели определяются как корни t_g уравнения:

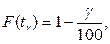(1.1)

где F(t) – функция распределения наработки до отказа (ресурса, срока службы). В частности, гамма-процентную наработку до отказа t_g определяют из уравнения 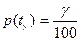, где р(t) – вероятность безотказной работы.

Как видно из формулы (1) гамма-процентные показатели равны квантилям соответствующих распределений. Если вероятности, отвечающие этим квантилям, выражают в процентах, то для показателей безотказности обычно задают значения 90; 95; 99; 99,5 % и т. д.

Тогда вероятность возникновения отказа на отрезке [0; t_g] будет составлять 0,10; 0,05; 0,01; 0,005 и т. д. Задаваемые значения g для критических отказов должны быть весьма близки к 100 %, чтобы сделать критические отказы практически невозможными событиями. Для прогнозирования потребности в запасных частях, ремонтных мощностях, а также для расчета пополнения и обновления парков машин, приборов и установок могут потребоваться гамма-процентные показатели при более низких значениях g, например, при g = 50 %, что приближенно соответствует средним значениям.

Статистические оценки для гамма-процентных показателей могут быть получены на основе статистических оценок либо непосредственно, либо после аппроксимации эмпирических функций подходящими аналогичными распределениями. Необходимо иметь в виду, что экстраполирование эмпирических результатов за пределы продолжительности испытаний (наблюдений) без привлечения дополнительной информации о физической природе отказа может привести к значительным ошибкам.

Средний ресурс, средний срок службы равны математическим ожиданиям соответствующих случайных величин наработки до отказа ресурса, срока службы.

Среднюю наработку до отказа Т₁ вычисляют по формуле:

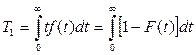, (1.2)

где F(t) – функция распределения наработки до отказа;

f(t) – плотность распределения наработки до отказа.

Т₁ может быть выражена через вероятность безотказной работы:

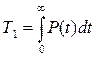, (1.3)

Статистическая оценка для средней наработки до отказа определяется по формуле:

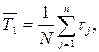(1.4)

где N – число работоспособных объектов при t = 0;

t_j – наработка до первого отказа каждого из объектов.

Показатели безотказности

Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ объекта не возникнет.

Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находится в работоспособном состоянии. Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем просто наработкой). Возникновение первого отказа – случайное событие, а наработка t от начального момента возникновения этого события – случайная величина. Вероятность безотказной работы р(t) объекта в интервале от 0 до t включительно определяют как:

p(t) = p( 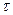; t), (1.5)

Здесь р(..) – вероятность события, заключенного в скобках. Вероятность безотказной работы р(t) является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой.

Если способность объекта выполнять заданные функции характеризуется одним параметром n, то вместо (1.5) имеем формулу:

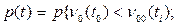
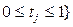, (1.6)

где n и n₀₀ – предельные условия работоспособности значения параметров (эти значения, вообще, могут изменяться во времени)

Вероятность безотказной работы р(t) связана с функцией распределения F(t) и плотностью распределения f(t) наработки до отказа:

F(t) = 1 – p(t); 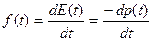, (1.7)

Наряду с понятием вероятность безотказной работы часто используют понятие «вероятность отказа», которое определяется следующим образом. Это вероятность того, что объект откажет хотя бы одни раз в течение заданной наработки, будучи работоспособным в начальный момент времени. Вероятность отказа на отрезке от 0 до t определяют по формуле:

Q(t) = 1 – p(t) = F(t), (1.8)

Точечные статистические оценки для вероятности безотказной работы 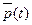от 0 до t и для функции распределения наработок до отказа 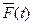даются формулами:

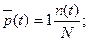
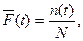(1.9)

где N – число объектов, работоспособных в начальный момент времени;

n(t) – число объектов, отказавших на отрезке от 0 до t.

Для получения достоверных оценок объем выборки N должен быть достаточно велик.

Определение безотказной работы в соответствии с формулами (1.5) и (1.6) относится к объектам, которые должны функционировать в течение некоторого конечного отрезка времени. Для объектов одноразового (дискретного) применения вероятность безотказной работы определяют как вероятность того, что при срабатывании объекта отказ не возникает.

Гамма-процентная наработка до отказа – наработка, в течение которой отказ объекта не возникает с вероятностью g, выраженное в процентах.

Средняя наработка до отказа – математическое ожидание наработки объекта до первого отказа.

Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.

Суть и содержание и формула для расчета этих параметров уже рассмотрены ранее.

Интенсивность отказов – показатель надежности невосстанавливаемых изделий, условная плотность, вероятности возникновения отказа объекта при условии, что до рассматриваемого момента времени отказ не возник.

Интенсивность отказов определяют по формуле:

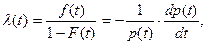(1.10)

Для высоконадежных систем p(t) » 1, так что интенсивности отказов приближенно равна плотности распределения наработки до отказа.

Статистическая оценка для интенсивности отказов 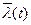имеет вид:

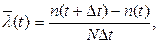(1.11)

где использованы те же обозначения, что и в формуле (1.9).

Параметр потока отказов – параметр надежности восстанавливаемых объектов, равный отношению математического ожидания числа отказов восстанавливаемого объекта за достаточно малую наработку к значению этой наработки.

Параметр потока отказов m(t) определяют по формуле:

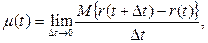(1.12)

где Dt – малый отрезок наработки;

r(t) – число отказов, наступивших от начального момента времени до достижения наработки t. Разность r(t + Dt) – r(t) представляет собой число отказов на отрезке Dt.

Наряду с параметром потока отказов в расчетах и обработке экспериментальных данных часто используют осредненный параметр потока отказов.

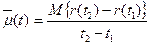(1.13)

По сравнению с формулой (12) здесь рассматривается число отказов за конечный отрезок [t₁, t₂], причем t₁ £ t £ t₂. Если поток отказов стационарный, то параметры, определяемые по формуле (1.12) и (1.13), от t не зависят.

Статистическую оценку для параметра потока отказов m(t) определяют по формуле:

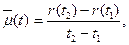(1.14)

которая по структуре аналогична формуле (1.13). Для стационарных потоков можно применять формулу:

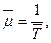(1.15)

где 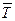– оценка для средней наработки на отказ.

Показатели ремонтнопригодности и сохраняемости

Вероятность восстановления – вероятность того, что время восстановления работоспособного состояния объекта не превысит заданное значение.

Гамма-процентное время восстановления – время, в течение которого восстановление работоспособного объекта будет осуществлено с вероятностью g, выраженной в процентах.

Среднее время восстановления – математическое ожидание времени восстановления работоспособного состояния объекта после отказа. Иначе, среднее время вынужденного нерегламентированного простоя, вызванного отысканием и устранением одного отказа.

Интенсивность восстановления – условная плотность вероятности восстановления работоспособного состояния объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено.

Средняя трудоемкость восстановления – математическое ожидание трудоемкости восстановления объекта после отказа.

Гамма-процентный срок сохраняемости – срок сохраняемости, достигаемой объектом с заданной вероятностью g, выраженной в процентах.

Средний срок сохраняемости – математическое ожидание срока сохраняемости.

Комплексные показатели надежности.

Показателем, определяющим долговечность системы, объекта, машины, может служить коэффициент технического использования.

Коэффициент технического использования –отношение математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и всех простоев для ремонта и технического обслуживания:

Коэффициент технического использования, взятый за период между плановыми ремонтами и техническим обслуживанием, называется коэффициентом готовности, который оценивает непредусмотренные остановки машины и что плановые ремонты и мероприятия по техническому обслуживанию не полностью выполняют свою роль.

Коэффициент готовности –вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Физический смысл коэффициента готовности – это вероятность того, что в прогнозируемый момент времени изделие будет исправно, т. е. оно не будет находиться во внеплановом ремонте.

Коэффициент оперативной готовности –вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.

Классификация показателей. В зависимости от способа получения показатели подразделяют на расчетные, получаемые расчетными методами; экспериментальные, определяемые по данным испытаний; эксплуатационные, получаемые по данным эксплуатации.

В зависимости от области использования различают показатели надежности нормативные и оценочные.

Нормативными называют показатели надежности, регламентированные в нормативно-технической или конструкторской документации.

К оценочным относят фактические значения показателей надежности опытных образцов и серийной продукции, получаемые по результатам испытаний или эксплуатации.