Основной закон зацепления

Идея основной теоремы зацепления была высказана английским ученым Р. Виллисом в 1841 г. при разработке классификации механизмов на основе на основе анализа отношения скоростей звеньев.

Пусть передача между двумя осями О₁ и О₂ с угловыми скоростями ω₁ и ω₂ осуществляется посредством 2-х взаимоогибаемых кривых К₁ и К₂ (рисунок 4.22, а).

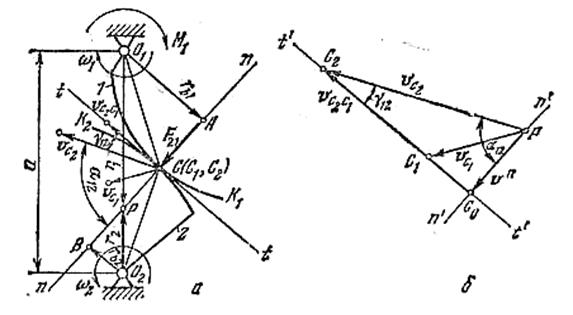
а - схема механизма с высшей парой; б - план скоростей.

Рисунок 4.22 - К выводу основного закона зацепления

Проведем в точке соприкосновения С кривых К₁ и К₂ и нормаль n-n и касательную t-t к этим кривым. В точке С соединяются две кривые, поэтому будут две точки: С₁, принадлежащая кривой К₁, и С₂, принадлежащая кривой К₂. Скорость точки С₁ известна по величине и направлению. Определим скорость точки С₂ методом планов (см. гл.2, §2.4, п.2.4.2). Выбираем масштабный коэффициент плана сил μ_V = V_C1/[P_VC₁] = ( 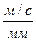). Записываем векторное уравнение плана скоростей

V_C2=V_C1+V_C2C1|| t-t

V_C2=V_O2+V_C2O2^ СО₂.

Построенный план скоростей представлен на рисунке 4.22, б.

Из точек О₁ и О₂ опускаем на нормаль перпендикуляры О₁А и О₂В, а из полюса плана скоростей опустим перпендикуляр Р_Vc_o на линию действия скорости V_C2C1. Отрезок P_Vc_o представляет собой нормальную составляющую V_n векторов скоростей V_C1 и V_C2, т.е. V_Co=V_A± V_B=V_n.

Рассмотрим треугольники ΔО₁АС₁ и ΔР_VС_оС₁ – они подобны по взаимно-перпендикулярным сторонам, т.е.

ΔО₁АС₁~ΔР_VС_оС₁.

Аналогично ΔО₂BС₂~ΔР_VС_оС₂.

Исходя из этого, составим пропорции:

О₁А/О₁С₁=[Р_VС_о]/Р_VС₁;

О₂В/О₂С₂=[Р_VС_о]/Р_VС₂.

Выразим из этих уравнений Р_VС_о:

Р_VС_о=О₁А [Р_VС₁]/О₁С₁;

Р_VС_о=О₂В [Р_VС₂]/О₂С₂.

Эти равенства можно записать в действительных скоростях:

V_Со = О₁А V_С1/О₁С₁;

V_Со= О₂В V_С2/О₂С₂.

Приравняем правые части уравнений:

О₁А V_С1/О₁С₁=О₂В V_С2/О₂С₂.

Скорости точек С₁ и С₂ вычисляются по формулам V_С1 =ω₁О₁С₁, V_С2=ω₂ О₂С₂. С учетом этого, имеем:

О₁А ω₁ О₁С₁/О₁С₁ = О₂В ω₂ О₂С₂/О₂С₂.

После сокращения, получим следующее выражение

О₁А ω₁ = О₂В ω₂.

Отношение угловых скоростей есть передаточное отношение. В итоге получим формулу:

ω₁/ω₂ = О₂В/О₁А = R_W2/R_W1 = z₂/z₁ = U₁₂, (4.15)

где R_W1 и R_W2 - радиусы начальных окружностей колес.

Равенство (4.15) называется основным законом зацепления, который гласит: нормаль в точке касания высшей кинематической пары качения и скольжения делит линию центров на части, обратно пропорциональные угловым скоростям.

Точка р, делящая линию центров О₁О₂ на части, обратно пропорциональные угловым скоростям, называется полюсом зацепления. Тогда межосевое расстояние a_W будет равно