Неравномерность движения механизмов

До сих пор исследование движения механизмов проводилось с учетом, если угловая скорость ведущего звена была постоянной. На самом деле скорость кривошипа при установившемся движении является переменной величиной (§2, п. 3.2.1). Колебания скоростей вызывают в кинематических парах дополнительные динамические нагрузки. Это, в свою очередь, приводит к понижению общего КПД механизма и надежности его работы, к ухудшению технологического процесса.

Рассматривая колебания скорости ведущего звена, можно обнаружить, что эти колебания бывают двух различных типов:

Ø Периодические колебания – такие колебания, при которых через каждый полный цикл установившегося движения кинетическая энергия механизма принимает первоначальное значение, и скорости ведущего звена периодически повторяются с одним и тем же циклом.

Ø Непериодические колебания – такие колебания, при которых колебания скоростей не имеют определенного цикла. Непериодические колебания вызваны различными причинами: внезапное изменение полезных или вредных сопротивлений, включение в механизм дополнительных масс и др.

Во многих механизмах наблюдается оба вида колебания скоростей. Колебания скоростей могут достигнуть такой величины, которая не допустима с точки зрения работы механизма. Тогда возникает задача о регулировании колебаний скоростей при установившемся движении, которую мы рассмотрим в п. 2.4 этой же главы.

3.2.3.1. Средняя скорость механизма и его коэффициент

неравномерности движения

Для изучения периодических колебаний скоростей во время установившегося движения необходимо знать среднюю скорость механизма. Т.к. скорость меняется от минимального значения до максимального, то средняя скорость будет равна средней арифметической

ω_ср=(ω_max+ω_min)/ 2. (3.67)

На паспорте двигателя такая скорость обычно указывается как номинальная.

Отношение разности максимальной и минимальной скоростей к среднему значению, называется коэффициентом неравномерности движения механизма δ

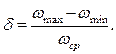(3.68)

Формула (3.68) показывает: чем меньше разность между ω_max и ω_min, тем равномернее вращается ведущее звено.

а) б)

ω ω

ω_max

ω_min ω_ср

2π φ 2π φ

а - с плавным изменением угловой скорости; б - менее плавным.

Рисунок 3.18 - Графики зависимости угловой скорости от угла поворота

Физический смысл коэффициента неравномерности δ. Коэффициент неравномерности движения характеризует только перепад угловой скорости ведущего звена в пределах от ω_min до ω_max, но не показывает динамику движения внутри одного полного цикла периода установившегося движения, т.е. не зависит от частоты колебаний. На рисунке 3.18 показаны два графика зависимости ω = ω(φ), у которых ω_max и ω_min равны, но угловые ускорения для графика б) значительно больше. Поэтому и динамические характеристики различны, т.е. различны кинетическая энергия, момент инерции и др. Коэффициент неравномерности рассчитан для некоторого вида машин. Для каждого вида машин имеется своя допустимая величина δ, выработанная практикой. Для двигателей внутреннего сгорания δ = 0,0125- 0,006; для насосов δ = 0,2 - 0,03; для сельхозмашин δ = 0,1- 0,02 и т.д. Наилучшие условия работы всех машин – абсолютно равномерное вращение их главного вала (ведущего звена), т.е. когда δ = 0. Допустимые δ приводятся в справочной литературе и учебных пособиях по расчету механизмов. В частности, δ приводятся в источнике [1] данного пособия.

Теперь рассмотрим зависимость коэффициента неравномерности от момента инерции, кинетической энергии и от угловой скорости.

3.2.3.2 Связь между приведенным моментом инерции, кинетической

энергией, средней угловой скоростью и коэффициентом

неравномерности движения механизма

Выразим из формулы (3.66) значения ω_max и ω_min:

ω_max = 2ω_ср - ω_min

ω_min = 2ω_ср - ω_max (а)

Теперь из формулы (3.67) выразим эти же значения:

ω_max = δω_ср + ω_min

ω_min = ω_max - δω_ср (б)

Приравняем формулы (а) и (б):

2ω_ср- ω_min = δω_ср+ ω_min

2ω_ср- ω_max = ω_max - δω_ср

После преобразования получим:

2ω_min=2ω_ср- δω_ср

2ω_max=2ω_ср+ δω_ср

Разделим обе части обоих уравнений на 2:

ω_min=ω_ср- δω_ср/2

ω_max=ω_ср+ δω_ср/2

и вынесем за скобки ω_ср:

ω_min=ω_ср(1+δ/2)

ω_max=ω_ср(1-δ/2)

Возведем обе части этих уравнений в квадрат:

ω²_min=ω²_ср(1-δ+δ²/4)

ω²_max=ω²_ср(1-δ+δ²/4)

При малых значениях коэффициента δ членом δ²/4 можно пренебречь

ω²_min=ω²_ср(1+δ)

ω²_max=ω²_ср(1-δ) (в)

Запишем уравнение приведенного момента инерции через кинетическую энергию (формула 3.53):

J^max_пр=2Т/ω²_max

J^min_пр=2Т/ω²_min (г)

Подставим формулы (в) в уравнения (г)

J^max_пр=2Т/ω²_ср(1+δ)

J^min_пр=2Т/ω²_ср(1-δ) (3.69)

Формулы (3.69) отображают зависимость кинетической энергии от приведенного момента инерции Т = Т(J_пр), которая может изображаться графически. График зависимости Т = Т(J_пр) называется графиком энергия-масса или диаграммой Ф. Виттенбауэра, названной по имени русского ученого. В дальнейшем мы рассмотрим ее построение.

3.2.3.3 Маховик и его физический смысл

В установившемся режиме работают очень многие машины – станки, прессы, прокатные станы, лесопильные рамы, текстильные машины, генераторы электрической энергии, компрессоры, насосы и т.д. Наилучшее условие для работы всех этих машин – абсолютно равномерное вращение их главного вала (принимаемого обычно в качестве ведущего звена). Колебания скорости главного вала вызывают дополнительные нагрузки, вследствие чего снижаются долговечность и надежность машин. Но поскольку колебания скорости полностью устранить невозможно, нужно хотя бы по возможности сократить их размах. Иными словами, значение коэффициента неравномерности δ надо сделать приемлемо малым. Рассмотрим, каким образом можно решить эту задачу.

Все звенья механизма обладают инертностью. Чем инертнее материальное тело, тем медленнее происходят изменения его скорости.

Уравнения (3.69) показывают, что при уменьшении величины δ возрастает приведенный момент инерции J_пр механизма, а, следовательно, его масса и кинетическая энергия. Поэтому увеличение равномерности движения ведущего звена может быть достигнуто за счет увеличения приведенного момента инерции механизма. Увеличение приведенных масс или приведенных моментов инерции ведет за собой увеличение масс отдельных звеньев механизма. На практике это увеличение производится посадкой на один вал машины добавочной детали, имеющий заданный момент инерции. Эта деталь носит название махового колеса или маховика.

Задачей маховика является уменьшение амплитуды периодических колебаний скорости ведущего звена, обусловленных свойствами самих механизмов или периодическим изменением соотношений между величинами движущих сил и сил сопротивлений. Подбором массы и момента инерции маховика можно заставить ведущее звено двигаться с заранее заданным отклонением от некоторой его средней скорости.

Маховик является аккумулятором кинетической энергии механизма. Он накапливает ее во время ускоренного движения и отдает обратно во время замедления механизма. Такая аккумулирующая роль маховика позволяет использовать накопленную им энергию для преодоления повышенных полезных нагрузок без увеличения мощности двигателя.

Физически роль маховика в машине можно представить следующим образом. Если в пределах некоторого угла поворота ведущего звена работа движущих сил больше работы сил сопротивления (А_дв.с.>А_с.с), то ведущее звено вращается ускоренно и кинетическая энергия увеличивается. При наличии в машине маховика приращение кинетической энергии распределяется между массами звеньев механизма и массой маховика, а при его отсутствии все приращение кинетической энергии должно быть отнесено к массам звеньев механизма. Если же А_дв.с.< А_с.с, то ведущее звено вращается замедленно и кинетическая энергия уменьшается.

Форма маховика может быть любой. Но по конструктивным соображениям наиболее удобной является форма в виде диска с тяжелым ободом, колесо со спицами (рисунок 3.20) или другая форма, симметричная относительно главных осей инерции. Это позволяет избежать дополнительных давлений на вал подшипника, на который насажен маховик.

Итак, чтобы определить размеры махового колеса, нужно знать его массу, а та, в свою очередь, зависит от момента инерции маховика. Существует несколько способов определения момента инерции маховика. Мы остановимся только на двух.

3.2.3.4 Приближенный метод определения момента

инерции маховика

Уравнение движения механизма можно записать в форме уравнения кинетической энергии:

А_дв.с.-А_с.с= .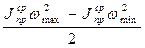

Изменение кинетической энергии есть разность работ, которая в свою очередь равна работе, т.е.:

ΔТ = А_дв.с.- А_с.с = А.

Тогда

А= ,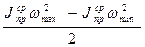

где J^ср_пр есть среднее значение приведенного момента инерции. Вынесем его за скобку:

А= .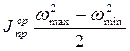

Учитывая, что

ω²_max - ω²_min=(ω_max+ω_min)(ω_max-ω_min)

и, принимая во внимание формулы (3.66), (3.67), получим выражение для работы

А= 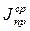ω²_ср δ.

Если пренебречь изменением момента инерции механизма и представив, что 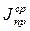= 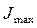, то можно вычислить момент инерции маховика приближенно

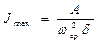. (3.70)

В этой формуле изменение момента инерции механизма не учитывается, он принимается постоянной величиной. Более точным является определение момента инерции маховика методами Н.И. Мерцалова и К.Э. Рериха. Эти методы подробно рассмотрены в источнике [3] данного пособия. Еще одним методом, позволяющим более точно определить J_мах является метод профессора Ф. Виттенбауэра. Его мы рассмотрим более подробно.

3.2.3.5 Определение момента инерции маховика

методом Ф.Виттенбауэра

Ключом для определения J_мах этим методом является построение графика энергия-масса или диаграммы Ф.Виттенбауэра (см. гл. 3, §2, п. 3.2.3.2). Для этого строится зависимость момента инерции от кинетической энергии J_пр= J_пр (ΔТ). При определении момента инерции маховика заданным является коэффициент неравномерности, силы же инерции не должны входить в диаграммы движущих сил и сил сопротивления. Средняя угловая скорость ведущего звена должна равняться истиной (формула 2.21, гл. 2, п. 2.3.3)

ω_ср = ω₁ =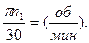

Порядок проведения метода Ф. Виттенбауэра

1. Строится механизм в n положениях, начиная с «мертвого» (гл.2, §2 и §3, п. 3.3). Для каждого положения (в нашем примере в 6-ти) строится план скоростей и план ускорений.

2. Рассчитываются внешние силы, действующие на звенья механизма. В частности для двигателя внутреннего сгорания вычисляются силы давления газа на поршень Р_Г по формуле (3.2).

3. Для каждого положения вычисляется приведенная сила (формула 3.48):

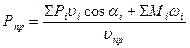= (Н).

Также Р_пр можно вычислить по методу Н.Е.Жуковского (гл.3, §3.1, п. 3.1.7), тогда Р_пр= -Р_ур (там же, п. 3.1.9).

4. Для каждого положения вычисляется приведенный момент от движущихся сил или от сил сопротивления, смотря какое движение совершает ведущее звено – ускоренное или замедленное (там же):

М_пр=Р_прℓ_ОА=(Нм).

5. Строится график приведенного момента от движущихся сил (в нашем примере движение ускоренное). Для этого высчитываем масштабный коэффициент приведенного момента:

μ_Мпр=М_пр1/h₁=(Нм/мм).

И рассчитываем амплитуды приведенных моментов в мм:

h₂ = М_пр2/μ_Мпр, μ_Мпр = М_пр1/h₁ и т.д.

Проводим оси М_пр и φ. Ось φ делим на 6 равных частей и откладываем высоты h₁, h₂ и т.д. Соединяем их плавной линией (рисунок 3.19, а).

6. Методом графического интегрирования строим график работы движущих сил А_дв.с. (рисунок 3.19, б). Соединяя начало графика с его концом, получаем график работы сил сопротивления А_с.с. (для замедленного движения наоборот).

7. Строится график изменения кинетической энергии, как разность работ (рисунок 3.19, в):

ΔТ = А_дв.с.- А_с.с. (3.71)

Высчитываются масштабные коэффициенты полученных графиков

μ_А=μ_ΔТ = μ_Мпрμ_φН =(Дж/мм),

где Н – полюсное расстояние в мм.

8. Считаем для каждого положения осевой приведенный момент инерции по формуле 3.55 (гл. 3, § 3.1, п. 3.1.9):

J_пр = 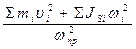= (кгм²).

9. Строим график J_пр, повернутый на 90^о, чтобы ось φ стала вертикальной (рис. 3.19, г). Для его построения высчитываем масштабный коэффициент

μ_Jпр=J_пр1/Х₁=(кгм²/мм).

10. На пересечении графиков J_пр и ΔТ строится диаграмма Виттенбауэра (график энергия-масса), исключая параметр φ.

11. Определяем углы ψ_max и ψ_min. Т.к. по оси абсцисс отложен приведенный момент инерции J_пр в масштабе μ_Jпр, а по оси ординат ΔТ в масштабе μ_ΔТ, то

tgψ = y/x = Тμ_Jпр /J_прμ_ΔТ.

Откуда выразим соотношение, учитывая углы для каждой касательной

Т/J_пр =μ_ΔТtgψ_max/μ_Jпр

Т/J_пр =μ_ΔТtgψ_min/μ_Jпр (а)

Зная формулу кинетической энергии (Т=J_прω²/2), определим отношение

Т/J_пр=ω²_max /2

Т/J_пр=ω²_min /2 (б)

Приравнивая выражения (а) и (б) и выразив угловую скорость, получим

ω²_max =2μ_ΔТtgψ_max/μ_Jпр

ω²_min=2μ_ΔТtgψ_min/μ_Jпр (в)

В формулы (в) из п. 3.2.3.2

ω²_min= ω²_ср(1+ δ); ω²_max= ω²_ср(1- δ)

подставим полученные соотношения, и, выразив углы, имеем:

tgψ_max= μ_Jпрω²_ср (1+δ)/2μ_ΔТ

tgψ_min= μ_Jпрω²_ср (1-δ)/2μ_ΔТ (3.72)

12. Находим отрезок [kℓ]. Для этого проводим касательные к диаграмме ΔТ = f(J_пр) под углами ψ_max и ψ_min (рис. 3.19, д). Пересечение их с вертикальной осью φ даст нам отрезок [kℓ].

13. Определяем момент инерции маховика J_мах.

J_мах = 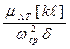= (кгм²), (3.73)

где [kℓ] - отрезок в мм. Формула (3.73) позволяет с необходимой точностью определить момент инерции маховика J_мах.

При подсчете углов ψ_max и ψ_min по формулам 3.72 может оказаться, что они будут очень велики. Пересечение касательных с осью ординат диаграммы ΔТ = f(J_пр) получится внизу, вне пределов чертежа. Поэтому из конструктивных соображений необходимо изменить углы до 45^о – 60^о.

График приведенного осевого Графики приведенных моментов

момента инерции J_пр от движущихся сил М_пр^дв.с. и от сил

сопротивления М_пр^с.с.

μ_Jпр=(кгм²/мм) μ_Мпр=…= (Нм/мм)

г) а) μ_φ=…= (рад/мм)

0 0 J_пр М_пр

х₁

1 х₂ 1 h₂

2 2 М_пр^с.с. h₅

Р

3 3 0 1 2 3 4 5 6 φ

4 4 h₁

5 5 Н h₄

М_пр^дв.с.

6 6 б) Графики работы движущихся сил А_дв.с.

и сил сопротивления А_с.с.

φ А μ_А=…= (Дж/мм)

A_с.с.

0 1 2 3 4 5 6 φ

А_дв.с.

Диаграмма Ф.Виттенбауэра График изменения кинетической

(график энергомасс) энергии ΔТ

д) в) μ_ΔТ =…= (Дж/мм)

ΔТ

ψ_max

3

k 0,6 0 1 2 3 4 5 6 φ

4 5

2 1 ψ_min

ℓ ψ_max

ψ_min

Рисунок 3.19 - Построение диаграммы Ф. Виттенбауэра

Метод Ф.Виттенбауэра не учитывает влияние скорости на действующие силы и моменты. Так график приведенного момента от движущих сил построен в виде зависимости от угла поворота ( 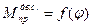), а не от угловой скорости 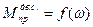. Пренебрежение влиянием скорости на силы и моменты допустимы по той причине, что скорость ведущего звена отклоняется от среднего значения не более чем на ± 2 %. Поэтому изменения сил и моментов, приложенных к ведущему звену и зависящих от скорости, также будут небольшими и ими можно пренебречь.

Если известен момент инерции маховика, можно определить его размеры.

3.2.3.6 Определение размеров махового колеса

Размеры маховика зависят от его установки в машине. Если маховик закрепляется на валу ведущего звена, то его момент инерции равен вычисленному. В некоторых случаях маховик устанавливается на ведомом валу. В этом случае найденный расчетом момент инерции будет являться приведенным моментом инерции маховика. Зная J_мах можно рассчитать размеры маховика для различных типов.

а) Маховик выполнен в виде сплошного диска со ступицей (рисунок 3.20, а).

Диаметр этого вида маховика вычисляется по формуле

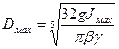=(м). (3.74)

а) б)

h

d_ст d_ст

D_мах D_мах

b b

b_ст b_ст

а – маховик в виде сплошного диска со ступицей;

б - в виде колеса со спицами

Рисунок 3.20 - Изображение маховика

б). Маховик выполнен в виде колеса со спицами (рисунок 3.20, б). При определении размеров такого вида маховика весом втулки и спиц пренебрегают, считая, что момент инерции маховика определяется только его ободом. Диаметр маховика будет вычисляться по формуле:

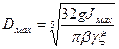=(м). (3.75)

В формулах (3.74) и (3.75) принято: J_мах - момент инерции маховика в кгм², γ = 93000 Н/м³ - удельная плотность, g = 9,8 м/с² - ускорение свободного падения, β=b/D_мах = 0,07…0,1 - отношение ширины обода к диаметру маховика, ξ = h/D_мах = 0,1…0,15 - отношение толщины обода к диаметру маховика.

Вопросы для самоконтороля

1. Что понимают под механическим КПД механизма?

2. Чему равен КПД при последовательном (параллельном) соединении механизмов?

3. Расскажите о причинах, вызывающих колебания скорости входного звена механизма.

4. Объясните назначение маховика в машине.

5. Выведите формулу для расчета момента инерции маховика при постоянном приведенном моменте инерции звеньев механизма.

6. Чем следует руководствоваться при выборе места установки маховика в машине?