Регулирование механизмов

3.2.4.1 Типы регуляторов. Задачи регулирования.

Основные схемы регулирования

Как было указано в п. 3.2.3 данной главы, колебания скоростей во время установившегося движения могут достигнуть такой величины, которая не допустима с точки зрения работы механизма. Тогда возникает задача об их регулировании.

Регулирование периодических колебаний при установившемся движении осуществляется подбором масс звеньев механизма. Этот вопрос мы будем рассматривать в п. 3.2.5. В случае непериодических колебаний скоростей при установившемся движении задача о регулировании скоростей решается установкой специальных механизмов – регуляторов.

Регулятор – механизм, регулирующий законы изменения движущих сил или сил сопротивления. Регулятор устанавливает равновесие между движущими силами и силами сопротивления.

Типы регуляторов:

1. Скоростные – реагируют на изменение скорости. Они подразделяются:

а) центробежные – регулируют центробежные силы инерции;

б) инерционные – регулируют тангенциальные силы;

в) модераторы – регулируют силы сопротивления.

Рисунок 3.21 - Схема прямого

регулирования

В результате этого происходит отклонение регулируемого параметра от заданного. Эти изменения воспринимаются чувствительным элементом 3, который передает необходимую информацию регулирующему органу 4, восстанавливающему заданный параметр у регулируемого объекта 1.

Схема 1-3-4-1 - носит название обратной связи. Регулируемый объект 1 посредством обратной связи воздействует на чувствительный элемент 3, который в свою очередь действует на регулируемый объект 1.

В машинном агрегате регулируемым объектом является двигатель, источником возмущения - рабочая машина.

Системы регулирования бывают:

1. Система прямого регулирования – регулятор непосредственно соединён с механизмом.

2. Система непрямого регулирования – между регулятором и механизмом подключают вспомогательный источник энергии – сервомотор.

Задачи регулирования – поддерживать в стационарном режиме изменение скорости, угловую скорость, температуру, давление и т. п.

Система прямого регулирования

На рисунке 3.22 показан машинный агрегат, состоящий из рабочей машины 2 и теплового двигателя 1. Чувствительным элементом является центробежный регулятор 3.

Регулятор 3 состоит из двух тяжёлых шаров К, сидящих на звеньях АС и ВD, которые входят во вращательные пары со звеньями СЕ и DF. А они входят во вращательные пары с муфтой N, которая свободно скользит вдоль направляющей z-z. Звенья АС и ВD связаны пружиной L, которая стремится сблизить шары. Регулятор 3 приводится в движение от ведущего звена посредством конической зубчатой передачи H-G. Регулятор вращается с угловой скоростью:

ω_p= ω₁U_1p,

где U_1P – передаточное отношение от ведущего звена к регулятору.

При различных угловых скоростях ω₁ муфта N занимает различные положения. С муфтой N соединен рычажный механизм, увеличивающий или уменьшающий подачу движущей энергии Р_д в двигатель. Рычажный механизм состоит из звеньев ОR и RT, и заслонки 4. В результате уменьшения сил полезных сопротивлений угловая скорость ω_р увеличилась. Шары К будут удаляться от оси вращения z-z и муфта N будет перемещаться вверх. Звено RT действует на заслонку 4, которая, опускаясь, уменьшает подачу Р_д. Когда движущие силы уменьшаются, то ω_р тоже станет меньше, муфта N переместится вниз, а заслонка вверх и т.д.

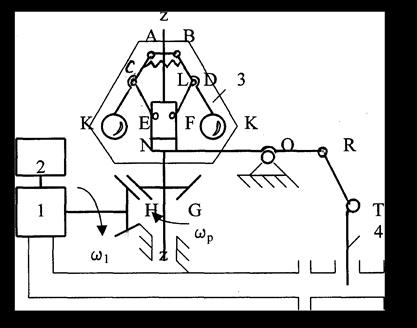
Рисунок 3.22 - Система прямого регулирования машинного агрегата

Следует отметить, что данный способ регулирования имеет некоторые недостатки. После уменьшения нагрузки угловая скорость оказывается выше той, которая была вначале, хотя движение машинного агрегата получается установившимся. Чтобы этого избежать, в технике применяются более сложные схемы регулирования.

Система непрямого регулирования

В предыдущем случае перемещение заслонки 4 осуществляется за счет центробежных сил шаров регулятора. В некоторых случаях этих сил бывает недостаточно для перемещения заслонки. Поэтому в систему регулирования включается дополнительный источник энергии – сервомотор.

На рисунке 3.23 показана система непрямого регулирования. Эта система имеет те же основные элементы, что и при прямом регулировании, но перемещение заслонки происходит посредством гидравлических сервомоторов 6 и 12.

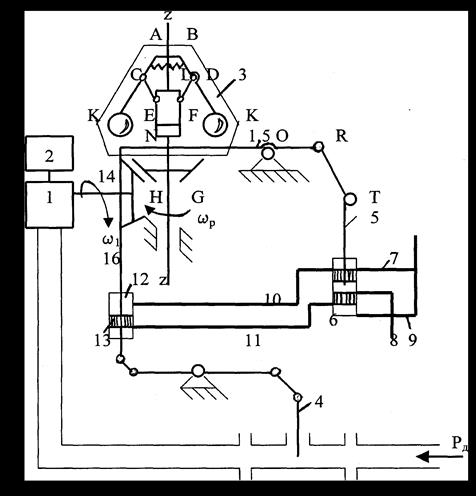
Рисунок 3.23 - Система непрямого регулирования

Теперь рассмотрим зависимость угловой скорости регулятора ω_p от высоты подъема z муфты N.

3.2.4.2. Кинетостатика центробежного регулятора

Угловая скорость регулятора ω_p для данного момента времени есть величина постоянная. Рассмотрим равновесие регулятора под действием всех внешних сил, в том числе и сил инерции, при этом силы трения равны нулю.

1.Силы приводятся к муфте N. На регулятор действуют силы: Р_И, -Р_И – силы инерции шаров; G₂ – силы тяжести шаров; G₁ – сила тяжести муфты; Р, -Р – силы сопротивления пружины. Если регулятор находится в равновесии под действием заданных сил, то должно иметь место равенство:

∑Р_i=0.

Определим приведенную к муфте силу Р_пр1 от сил тяжести и от сил сопротивления пружины. Для этого построим повернутый план скоростей механизма регулятора (рисунок 3.24) и составим уравнение моментов относительно полюса Р_υ:

∑М_Рυ= 0;

-G₁[Р_υn] - G₂[Р_υt]sinα - G₂[Р_υk]sinα - P[Р_υf]cosα - P[Р_υе]cosα + P_np1[Р_υn] = 0.

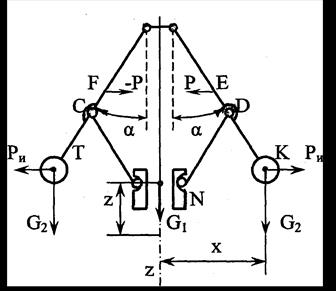
а - схема регулятора; б - повернутый план скоростей.

Рисунок 3.24 - К кинетостатическому исследованию центробежного

регулятора

Так как отрезки [Р_υt]=[Р_υk] и [Р_υf]=[Р_υе], то формула примет вид

P_np1[Р_υn] - G₁[Р_υn] - 2G₂[Р_υk]sinα - 2P[Р_υе]cosα = 0.

Выразим приведенную силу

P_np1= (G₁[Р_υn] + 2G₂[Р_υk]sinα + 2P[Р_υе]cosα)/[Р_υn].

Отрезки [Р_υn], [Р_υk] и [Р_υе] представляют собой в масштабе μ_υ величины скоростей υ_N, υ_K, υ_E, т.е. υ_N = [Р_υn]μ_υ, υ_K = [Р_υk]μ_υ, υ_E = [Р_υе]μ_υ, поэтому уравнение примет вид

P_np1 = G₁ + 2G₂(υ_K/υ_N)sinα + 2P(υ_E/υ_N)cosα. (3.76)

Определим Р_пр2 от сил инерции Р_и и –Р_и:

∑М_Рυ=0;

P_np2 [Р_υn] - Р_и [Р_υt]cosα - P[Р_υk]cosα = 0.

Или P_np2 = 2Р_и(υ_K/υ_N)cosα. (3.77)

Центробежная сила инерции вычисляется по формуле

Р_и = mω_p²x,

где х – переменное расстояние от центров тяжести шаров до оси регулятора. Тогда уравнение (3.76) примет вид:

P_np2 = 2mω_p²xcosα(υ_K/υ_N). (3.78)

Чтобы регулятор находился в равновесии, нужно, чтобы сумма приведенных сил была равна нулю:

∑Р_i = 0; Р_пр1+ Р_пр2 = 0. (3.79)

Приведенная сила Р_пр1 называется поддерживающей силой регулятора. Она зависит от сил тяжести G и от сил сопротивления пружины Р.

Приведенная сила Р_пр2 называется центробежной силой регулятора. Она зависит от сил инерции Р_и.

Подставим формулы (3.76) и (3.78) в выражение (3.79), учитывая, что приведенные силы Р_пр1 и Р_пр2 направлены в разные стороны. Получим

G₁+2G₂(υ_K/υ_N) sinα+2P(υ_E/υ_N)cosα-2mω_p²x cosα(υ_K/υ_N)=0

Введем обозначения: А=P_np2 /ω_p² =2mx cosα(υ_K/υ_N),

В = P_np1= G₁+ 2G₂ (υ_K/υ_N) sinα + 2P(υ_E/υ_N) cosα.

Получим

Аω_p² - В = 0. (3.80)

Уравнение (3.80) являетсяуравнением равновесия регуляторапри силах трения, равных нулю, когда силы приложены к муфте.

2. Силы приводятся к центру тяжести шаров Т и К. В некоторых случаях бывает удобнее силы, действующие на регулятор, приводить не к муфте, а к центру тяжести шаров, направляя их по линии центробежной силы инерции (рисунок 3.25). Обозначим: Р^΄_пр1 - приведенная к центру тяжести шаров поддерживающая сила (зависит от сил тяжести и от сил сопротивления пружины), Р^΄_пр2 - приведенная к центру тяжести шаров центробежная сила (зависит от сил инерции). Уравнение равновесия регулятора имеет вид:

Р^΄_пр1+ Р^΄_пр2 = 0.

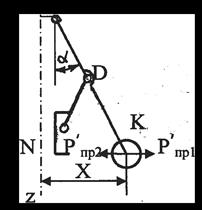
Рисунок 3.25 - Приведение сил

к центру тяжести шаров

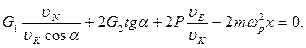(3.81)

Введем обозначения

С = Р^΄_пр1 = G₁υ_N/(υ_Kcosα)+2G₂tgα+2P(υ_E/υ_K);

D = Р^΄_пр2/ω_p² = 2mx.

и перепишем выражение (3.80), поменяв знаки

Dω_p² - С = 0. (3.82)

Уравнение (3.82) являетсяуравнением равновесия регуляторапри силах трения, равных нулю, когда силы приведены к центру тяжести шаров.

Рассмотрим зависимость угловой скорости регулятора от перемещения муфты, а также зависимость приведенных сил от переменного расстояния х.

3.2.4.3. Характеристика регулятора

Из формулы (3.80) выразим угловую скорость регулятора:

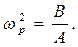(3.83)

Выражение (3.83) носит название равновесной угловой скорости регулятора, т.к. каждому положению муфты N соответствует вполне определенная угловая скорость.

Пользуясь уравнениями для А и В, а также формулой (3.83), можно построить диаграмму зависимости перемещения z муфты N от квадрата равновесной угловой скорости ω_p². Эта зависимость z = z(ω_p²) носит название равновесной диаграммы регулятора и представлена на рисунке 3.26.

Z C Р^΄_пр1

h i

z_i

0 x

ω²_min ω²_pi ω²_max ω²_p x_min x_max

Рисунок 3.26 - Равновесная диаграмма Рисунок 3.27 - Характеристика

регулятора регулятора

Пользуясь этой диаграммой можно определить значения максимальной и минимальной угловых скоростей, при которых муфта занимает свои крайние положения. Тогда средняя угловая скорость будет равна:

ω_ср = (ω_max+ω_min) /2.

Отношение разности квадратов угловых скоростей к удвоенному значению квадрата средней угловой скорости называется степенью неравномерности регулятора δ:

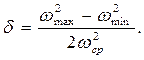(3.84)

Используя формулы для выражений С и D, можно построить диаграмму зависимости поддерживающей силы от переменного расстояния х, т.е. С = С(х) или Р^΄_пр1 = Р^΄_пр1(х). Такая зависимость носит название характеристики регулятора (рисунок 3.27).

3.2.4.4 Устойчивость регулятора

С помощью характеристики регулятора можно выяснить ряд важных свойств регулятора.

Если обратиться к равновесной диаграмме регулятора (рисунок 3.26), то можно заметить, что при z = 0 угловая скорость будет иметь наименьшее значение, а при z = h - максимальное значение. Поэтому, согласно диаграмме и формуле (3.83), степень неравномерности регулятора зависит от пределов скоростей, в которых может работать регулятор.

Известно, что величина центробежной силы вычисляется по формуле

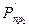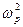= 2m x.

Сила 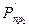на графике выглядит как прямая линия, проходящая через начало координат О (рисунок 3.28, а) и наклоненная к оси Ох под углом β, тангенс которого равен:

tgβ = (2m 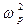xμ_x)/μ_p,

где μ_x, μ_p - масштабы построения диаграммы. Прямая Оm носит название линии центробежной силы.

a) б) в)

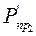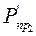
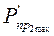Р^΄_пр1 Р^΄_пр1 Р^΄_пр1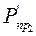

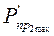
Р^΄_пр1 C

m Р^΄_пр1

C Р^΄_пр2 D Р^΄_пр1

Р^΄_пр2min Р^΄_пр2min

β D C

О x_c х x_min х x_min х

x_max x_max

а - исследование устойчивости регулятора; б - характеристика

статического регулятора; в - характеристика нестатического регулятора.

Рисунок 3.28 - Свойства регулятора

Построим в том же масштабе характеристику регулятора, т.е. зависимость Р^΄_пр1 = Р^΄_пр1(х), которая выразится кривой линией. Точка С пересечения прямой Оm с линией Р^΄_пр1 определяет то положение х_с центра груза, при котором регулятор находится в равновесном положении при постоянной угловой скорости ω_p, т.к. в этом положении равны по величине, но противоположны по направлению, силы Р^΄_пр1 и Р^΄_пр2. Таким образом, равновесие регулятора является устойчивым, если характеристика регулятора расположена так, что до точки С она лежит ниже линии центробежной силы, а после точки С она лежит выше линии центробежной силы. Т.к. регулятор должен работать в пределах, определяемых степенью неравномерности δ, то центробежные силы определяться:

Р^'_пр2max = 2mω²_maxx; Р^'_пр2min= 2mω²_minx.

Регулятор называется статическим, если до точки С ордината Р^'_пр1<Р^'_пр2, а после точки С ордината Р^'_пр1>Р^'_пр2. Такой регулятор устойчив для равновесных положений от x_min до x_max (рисунок 3.28, б).

Если условия устойчивости не выполняются на всем интервале от x_min до x_max (до точки С - Р^'_пр1>Р^'_пр2, а после точки С - Р^'_пр2<Р^'_пр2), то такой регулятор называетсянестатическим(рисунок 3.28, в).

3.2.4.5 Нечувствительность регулятора

До сих пор при рассмотрении равновесия регулятора мы не учитывали влияние сил трения. Сила трения всегда направлена в сторону, противоположную движению муфты. Следовательно, при подъеме муфты сила F_тр направлена вниз, а при опускании – вверх. Тогда в момент начала движения при подъеме муфты вверх будем иметь, учитывая условие равновесия (3.80), выражение:

А(ω^''_p)² - В - F_тр= 0.

Соответственно в момент начала движения муфты вниз получаем:

А(ω^'_p)² - В + F_тр = 0,

где ω^''_p - равновесная угловая скорость при подъеме, ω^'_p - равновесная угловая скорость при опускании. Выразим из этих уравнений равновесную угловую скорость. Получим:

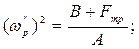
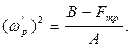(3.85)

Равновесная угловая скорость при отсутствии силы трения равна 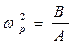- формула (3.82). Поэтому:

ω^'_p ≤ ω_p ≤ ω^''_p. (3.86)

Таким образом, для каждого положения муфты имеется некоторый интервал изменения угловой скорости, внутри которого положение муфты оказывается неизменным. Согласно выражениям (3.85) и (3.86) можно построить равновесные кривые для значений ω^'_p, ω_p, ω^''_p (рисунок 3.29).

Область, заключенная между кривыми ω^''_p² и ω^'_p², называется областью нечувствительности регулятора (показана штриховкой).

В этой области муфта регулятора остается неподвижной – регулятор не реагирует на изменение скорости.

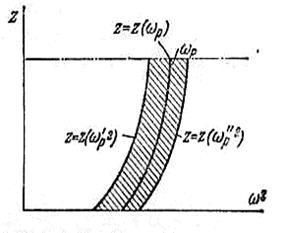
Рисунок 3.29 - Диаграмма, характеризующая

нечувствительность регулятора

ξ = F_тр/В. (3.88)

Итак, мы вкратце рассмотрели вопросы регулирования механизмов. Теперь рассмотрим уравновешивание звеньев механизма.

Вопросы для самоконтороля

1. Расскажите, что такое обратная связь в процессе автоматического регулирования.

2. Какие регуляторы относятся к статическим, а какие к нестатическим?

3. От чего зависит центробежная сила регулятора? Поддерживающая сила?

4. Что понимают под характеристикой регулятора скорости? В чем отличие устойчивой характеристики от неустойчивой?