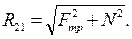Трение в поступательной кинематической паре

Пусть ползун движется по направляющей (рисунок 3.42). Ползун нагружен силой F, которая представляет собой результирующую всех действующих сил. Рассмотрим, при каких условиях ползун начнет двигаться.

Перенесем точку приложения силы F в точку О и разложим ее на составляющие: горизонтальную F^Iи вертикальную F^II. Обозначим угол, образуемый силой F и нормалью n-n через φ, то величины составляющих будут равны:

F^I= Fsinφ, F^II= Fcosφ.

Ползун сдвинется с места, когда F_тр= F^I. Сила нормального давления равняется вертикальной составляющей N = F^II. Тогда, по закону Кулона, имеем

F_тр= ƒN =ƒ F^II=ƒFcosφ.

Вместо F_тр подставим F^I, получим

F_тр= F^I= Fsinφ.

Приравняем оба эти равенства Fsinφ = ƒFcosφ. и выразим коэффициент трения ƒ = Fsinφ/Fcosφ. или, сократив F, имеем: ƒ = sinφ/cosφ = tgφ. ƒ=tgφ. (3.107) Итак, согласно формуле (3.107), ползун начнет движение, когда тангенс угла трения будет равен коэффициенту трения.

n φ

F^I О F_тр

F F^II

Рисунок 3.42

Определим реакцию в поступательной кинематической паре. Как указывалось в п. 1.3 данной главы, реакция в поступательной кинематической паре, при F_тр=0, направлена перпендикулярно движению ползуна и равна силе нормального давления (R₂₁=N). Теперь найдем реакцию, если F_тр¹0. Пусть ползун нагружен силой тяжести G (рисунок 3.43). Также действует сила Р,

которая перемещает ползун по направляющей. Задан угол трения φ. Тогда по закону Амонтона-Кулона сила трения будет равна: F_тр= ƒN. Реакция R₂₁является полной реакцией и будет раскладываться на две составляющие F_тр и N. Определим ее по теореме Пифагора

R₂₁ φ N

F_тр P

Рисунок 3.43

Учитывая закон Амонтона-Кулона и что ƒ= tgφ, получим

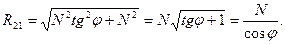
Или

R₂₁ cosφ =N. (3.108)

Из равенства (3.108) следует, что полная реакция в поступательной кинематической паре с учетом силы трения отклонена на угол трения в сторону силы трения.

При силовом расчете, чтобы определить реакцию в поступательной кинематической паре с учетом силы трения, задаются коэффициентом трения. Затем по формуле (3.107) определяют угол трения и проводят реакцию под этим углом. Остальные реакции определяют согласно п. 1.3 данной главы.

Конус трения Если давать силе F (R₂₁) различные направления в пространстве, то область равновесия будет ограничена конусом трения. Конус трения образуется вращением угла трения φ вокруг нормали n-n к соприкасающимся поверхностям (рисунок 3.44).

φ n

R₂₁ N

Рисунок 3.44

Итак, если тело движется поступательно, то направление приложенной силы должно проходить по стороне угла, равного 2φ, или по образующей конуса, раствор которого также равен 2φ.

<32 33 343536 37 38 >

Дата добавления: 2015-10-19; просмотров: 879;