Трение в винтовой кинематической паре

При рассмотрении трения в винтовой кинематической паре делают ряд допущений:

1. Т.к. закон распределения давлений по винтовой резьбе неизвестен, то считают, что давление гайки на винт и наоборот приложено по средней линии резьбы. Средняя линия резьбы расположена на расстоянии r от оси винта (рисунок 3.46).

2. Действие сил в винтовой паре сводится к действию сил на ползун, находящийся на наклонной плоскости. Для этого развертывают среднюю линию резьбы в плоскость.

Пусть на гайку действуют силы: сила тяжести G; сила Р, перпендикулярная к оси винта и необходимая для равномерного перемещения гайки; момент пары сил М, представленный в виде момента силы Р^¢, приложенной на расстоянии r^¢ от оси z-z. Также задан угол подъема наклонной плоскости α.

Чтобы гайка двигалась равномерно вдоль оси z-z, необходимо, чтобы момент М равнялся моменту силы относительно той же оси z-z, т.е.

Р^¢r^¢= Рr.

Составим уравнение равновесия всех сил, действующих на гайку

∑Р_i = 0, G + Р + N₂+ F_тр = 0.

r^΄ r z

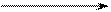
P^΄

a) б) в)

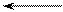
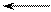
N N F_тр

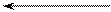
P α N

R₂₁ R₂₁

α F_тр α P G α φ

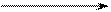
G P

G z

а – схема винтовой пары; б - развернутая винтовая линия

в плоскость с распределением сил; в - план сил.

Рисунок 3.46 - Трение в винтовой кинематической паре

Строим план сил (рисунок 3.46, в). Из плана сил определим:

Р = R₂₁sin (α+φ) Þ R₂₁ = P/sin(α+φ).

F_тр = R₂₁sinφ.

Подставим в формулу силы трения уравнение для реакции. Получим

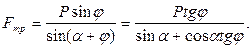
Зная, что tgφ =ƒ, имеем:

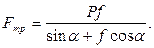(3.111)

Выражение (3.111) является формулой для определения силы трения в винтовой паре с прямоугольной резьбой. Уравнение для определения силы трения с треугольной резьбой выглядит как:

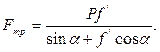(3.112)

где ƒ^΄- приведенный коэффициент трения ƒ^΄=ƒ/cosα. Так как ƒ^΄ >ƒ, то и сила трения в винтовой паре с треугольной резьбой больше, чем сила трения у прямоугольной резьбы.