Закон Кулона. Напряженность и потенциал электрического поля. Силовые линии

Взаимодействие заряженных тел регламентирует закон Кулона, установленный французским физиком Ш. Кулоном опытным путем с помощью изобретенных им крутильных весов в 1785 году: в вакууме сила взаимодействия между двумя точечными неподвижными зарядами пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой, соединяющей эти заряды, то есть

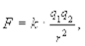(6.1)

где в СИ коэффициент пропорциональности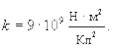

Окружающая среда влияет на взаимодействие зарядов: величина, которая показывает, во сколько раз сила взаимодействия между электрическими зарядами в данной среде меньше, чем в вакууме, называется диэлектрической проницаемостью среды (e), например, для воздуха e = 1,0006, для воды e = 81 и т. д. (существуют специальные таблицы).

Закон Кулона для точечных зарядов, погруженных в жидкий и газообразный диэлектрик, имеет вид

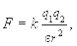(6.2)

Знак силы в уравнениях (6.1, 6.2) показывает ее направление относительно взаимодействующих зарядов, минус ¾ заряды притягиваются плюс ¾ отталкиваются. Обычно рассчитывают модуль силы взаимодействия, в этом случае соотношение (6.2) переписывается в виде:

(6.3)

Во многих задачах используют рационализированную форму записи закона Кулона

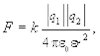(6.4)

где 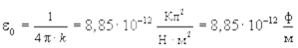и называется электрической постоянной.

Если взаимодействуют заряженные тела, размерами которых нельзя пренебречь по сравнению с расстоянием между ними (неточечные), то для нахождения силы их взаимодействия, эти тела мысленно разбивают на малые заряженные элементы (которые можно считать точечными) и рассчитывают кулоновские силы взаимодействия каждой пары зарядов, затем проводят векторное сложение этих сил.

Количественной характеристикой силового действия электрического поля на заряженные объекты служит векторная величина 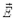¾напряженность электрического поля, которая равна силе, действующей на единичный положительный точечный заряд, помещенный в данную точку поля и которая направлена в сторону действия результирующей сил, приложенных к заряду. Если на точечный заряд q⁺(положительный) в некоторой точке поля действует сила 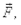то напряженность электрического поля в этой точке

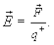(6.5)

Единицей измерения напряженности электрического поля в СИ является Н/Кл, или, как увидим в дальнейшем В/м, общепринятой является вольт на метр.

Рис. 6.1.

В случае создания электрического поля точечным зарядом q, его напряженность в точке N (см. рис. 6.1) определяется согласно (6.2), как

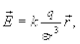(6.6)

где 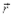¾радиус-вектор, проведенный в рассматриваемую точку N из точки, где находится заряд q, создающий поле.

Модуль вектора напряженности поля точечного заряда рассчитывается по формуле

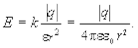(6.7)

Если электрическое поле создают несколько точечных источников (n), то его результирующая напряженность рассчитывается по принципу суперпозиции полей:

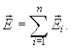(6.8)

Электрическое поле принято изображать с помощью линий напряженности. Это линии, касательные к которым в каждой точке совпадают с направлением вектора 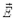в данной точке, а их густота пропорциональна модулю вектора 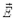в данном месте поля.

Примеры (рис. 6.2):

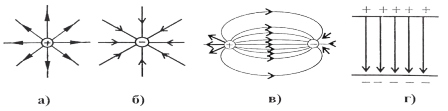
Рис. 6.2.

Электрическое поле, напряженность которого во всех точках одинакова по модулю и направлению, называется однородным. Его например, могут создать две разноименно заряженные плоские пластины (рис. 6.2, г).

Из соображений симметрии понятно, что равномерно заряженная сфера вне себя создает электрическое поле, аналогичное полю точечного заряда той же величины, что и заряд сферы q, если этот заряд поместить в центр сферы (рис. 6.3).

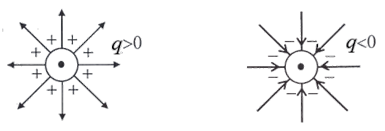
Рис. 6.3

Таким образом, формула (6.7) позволяет вычислить модуль вектора напряженности 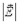в любой точке вне равномерно заряженной сферы.

Силы электростатического поля являются консервативными. Как известно, тело, помещенное в консервативное поле сил, обладает потенциальной энергией, которая определяется с точностью до определенной постоянной величины.

Энергия вносимого в поле заряда отсчитывается от бесконечности, то есть за границей действия электростатического поля, где принимается равной нулю. Энергетической характеристикой электростатического поля является потенциал.

Потенциалом электростатического поля j называют скалярную величину, численно равную потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Если и в данной точке поля точечный положительный заряд q⁺ имеет потенциальную энергию W_п то

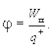(6.9)

Единица потенциала ¾ вольт (В), то есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж. Потенциал поля, созданного точечным зарядом q, равен

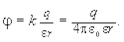(6.10)

При r = ¥, j = 0. Таким образом, потенциал ¾ это физическая величина, определяемая работой сил электростатического поля по перемещению единичного положительного заряда из данной точки поля в бесконечность.

Если поле создается несколькими зарядами (n), то потенциал поля системы зарядов будет равен алгебраической сумме потенциалов отдельных полей всех образующих систему зарядов:

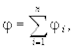(6.11)

считаем среду однородной по всем направлениям (e = const). При этом знак «+» приписывается потенциалу поля, созданного положительным зарядом, знак «-» ¾ отрицательным.

Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки 1 в точку 2, будет равна (см. соотношение 6.9):

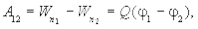(6.12)

где (j₁ - j₂) ¾ разность потенциалов двух точек 1 и 2 в электростатическом поле (она задается работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2).

Поскольку поле электростатических сил имеет консервативный характер, работа этих сил при переносе заряда по замкнутому контуру равна нулю.

Если мы обозначим через d расстояние между двумя очень близкими точками поля, принадлежащими одной силовой линии, то модуль вектора напряженности Е определяется как

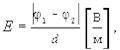(6.13)

где (j₁ - j₂) ¾ разность потенциалов между рассматриваемыми точками 1 и 2.

В однородном поле напряженность остается всегда постоянной, поэтому соотношение (6.13) справедливо для любых расстояний d между двумя точками одной и той же силовой линии. Если точки 1 й 2 принадлежат разным силовым линиям однородного электрического поля, то под d понимается проекция отрезка, соединяющего точки 1 и 2, на направление линий напряженности электрического поля.

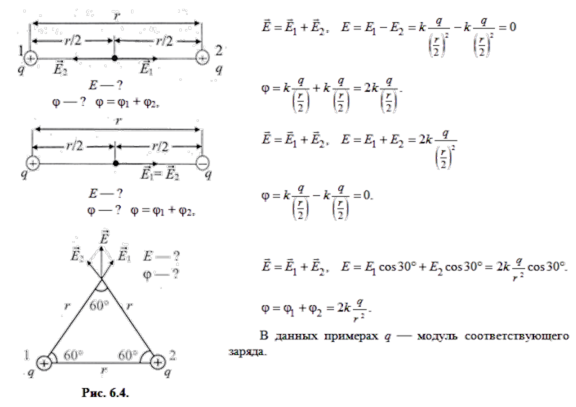
Примеры (рис. 6.4):