Электрическая емкость. Конденсаторы. Энергия электрического поля

Электрической емкостью (электроемкостью) уединенного проводника называют физическую величину, равную отношению заряда проводника к его потенциалу

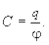(6.14)

Важно усвоить, что электроемкость не зависит от q и j(чем больше q, тем больше j), так как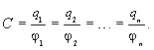

Электроемкость уединенного проводника определяется только его формой и размерами, а также электрическими свойствами окружающей диэлектрической среды, она измеряется в фарадах (1 Ф = 1 Кл/1 В).

Используя соотношение (6.10) получим выражение для электроемкости шара:

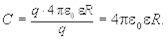(6.15)

Емкость уединенного проводника 1 Ф ¾ нереальная величина, такой емкостью обладает проводящий шар радиусом около 9 миллионов километров. На практике обычно используют: 1 мкФ = 10^-6 Ф, 1 пФ = 10^-12 Ф.

Из соотношения (6.15) следует, что e₀ измеряется в Ф/м.

Существуют устройства, способные накапливать (конденсировать) большие заряды, они представляют собой систему двух близко расположенных проводников, разделенных диэлектриком. Эти устройства называют конденсаторами. Проводящие поверхности конденсатора (обкладки) бывают плоскими (две близко расположенных пластины), а также могут иметь форму коаксиальных цилиндрических поверхностей или концентрических сфер.

На обкладках заряженного плоского конденсатора сосредоточены равные по модулю и противоположные по знаку заряды, однородное электрическое поле находится внутри конденсатора.

Электроемкостью конденсатора С называют отношение сообщенного обкладкам конденсатора заряда q к возникающей на них в результате этого разности потенциалов (j₁ - j₂):

(6.16)

где U ¾ сокращенное обозначение разности потенциалов.

Электроемкость плоского конденсатора зависит от его размеров:

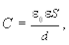(6.17)

где S ¾ площадь обкладки, d ¾ зазор между обкладками.

Электрическое поле обладает энергией и можно показать, что в диэлектрике с проницаемостью e плотность энергии электрического поля (т. е. энергии поля, приходящейся на единичный объем пространства) определяется выражением

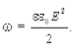(6.18)

Умножив w на объем конденсатора можно в конечном итоге получить формулы, определяющие энергию заряженного конденсатора

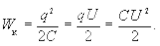(6.19)