Поверхностное натяжения. Капиллярные явления

Результирующая сил 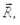действующих на некоторую молекулу, находящуюся внутри объема жидкости, со стороны окружающих молекул равна нулю (рис. 5.7). Если же молекула расположена на поверхностном слое жидкости, то на эту молекулу должна действовать сила 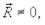стремящаяся переместить молекулу внутрь жидкости. Это приводит к тому, что жидкость принимает форму, при которой на ее поверхности располагается минимальное число молекул, т. е. поверхность жидкости становится наименьшей при отсутствии внешних сил. Такому условию отвечает шарообразная форма. Таким образом, поверхностный слой жидкости находится в состоянии натяжения и обладает запасом потенциальной энергии.

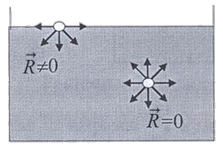
Рис. 5.7

Коэффициентом поверхностного натяжения называют величину, численно равную силе F, действующей на единицу длины линии l, ограничивающей поверхностный слой

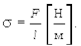(5.32)

Иногда коэффициент поверхностного натяжения рассчитывают как отношение потенциальной энергии поверхностного слоя к величине этой поверхности.

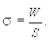(5.33)

Итак, поверхностное натяжение определяет форму жидкости, на границе раздела жидкость-среда. В зависимости от рода вещества, с которым граничит жидкость форма ее поверхности (мениск) может быть выпуклой и вогнутой (рис. 5.8).

Рис. 5.8

При этом, если угол q < 90°, то жидкость называется смачивающей. Если же q > 90°, то жидкость называется несмачивающей.

Выпуклый поверхностный слой давит на нижние слои жидкости, а вогнутый ¾ растягивает. Тем самым на жидкость со стороны изогнутого поверхностного слоя радиусом R оказывается избыточное давление, величина которого может быть рассчитана как

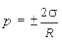(5.34)

Знак «+» соответствует выпуклому мениску, а «-» ¾ вогнутому мениску.

Избыточное давление вызывает заметное поднятие или опускание уровня жидкости в узких трубках (капиллярах). Высоту подъема жидкости в капиллярной трубке при полном смачивании ее стенок можно определить из соотношения

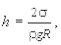(5.35)

где s¾коэффициент поверхностного натяжения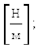

r¾плотность жидкости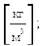

R ¾ радиус капиллярной трубки [м];

g¾ускорение свободного падения