Инерционное звено 2-го порядка.

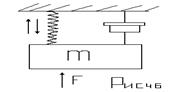Инерционное звено (И.З) 2-го порядка может быть получено при наличии двух соединённых емкостей, способных запасать энергию двух видов и взаимообмениваться этими количествами энергии. Примером такого звена могут служить масса, подвешенная на пружине и имеющая успокоительное устройство.

В этой системе (Рис.46) происходит обмен кинетической и потенциальной энергиями. Другим примером инерционное звено2-го порядка является энергетический контур (Рис.47).

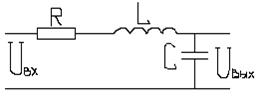Рис 47

В электрический контур входят индуктивность L, емкость С и активное сопротивление R. При подаче на вход контура входного напряжения Uвх в контуре происходит обмен электрической и магнитной энергией. Дифференциальное уравнение динамики для такого звена имеет вид:

Т₁²(d²x_вых/dt²)+ Т₂(dx_вых/dt)+x_вых=кх_вх

На практике может быть использована другая форма записи:

Т₁²(d²x_вых/dt²)+ αρТ(dx_вых/dt)+x_вых=кх_вх

При этом Т - постоянная времени, причем Т=Т2 , а переход для определения Т1 осуществляется так

Т1 =2ρТ, при этом ρ выступает как показатель колебательности. В операторной форме последнее дифференциальное уравнение (Д.У) имеет вид:

[Т²р²+αρТр+1]X_вых(Р)=кХ_вх(Р)

передаточная функция будет иметь вид:

W(P)=X_вых/Х_вх=1/[Т²р²+αρТр+1]

При подаче на вход звена единичного ступенчатого воздействия на его выходе мы получим колебательный переходный процесс(Рис 48,49).

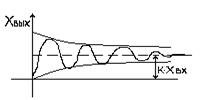
Рис 48 Рис.49

В зависимости от вида корней И.З 2-го порядка можно разделить на следующие звенья:

1)апериодическое Зв. 2-го порядка

2)колебательное Зв. 2-го порядка

3)консервативное звено .

В зависимости от этого будут меняться и частотные характеристики звеньев. В этом случае если мы имеем вещественные корни, уравнение будет соответствовать двум экспоненциальным составляющим

(Рис 50)

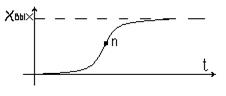
Рис.50

Как видно из рис.50 переходная характеристика апериодической без колебаний. В случае если мы имеем пару комплексных корней, переходная характеристика будет иметь вид представленный на Рис49, и мы будем иметь колебательное звено.

В том случае, если корни является мнимыми, мы будем иметь, консервативное звено 2-го порядка (Рис.51)

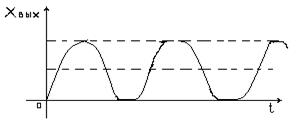Рис.51

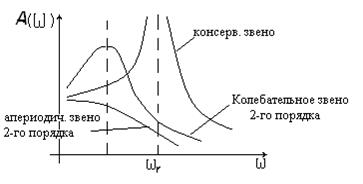
Рассмотрим частотные характеристики этих звеньев, АЧХ представлены на рис.52

На рис 53 представлены ФЧХ.

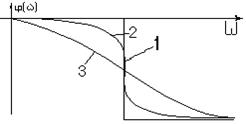Рис 53

1-Консервативное звено

2-Колебательное звено 2-го порядка

3- Апериодическое звено 2-го порядка

На рис 54 представлена АФХ:

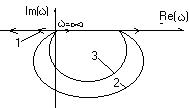
Из Рис 52 видно что на частоте ώr

АЧХ для консервативного звена имеет разрыв. При этом фаза сдвигается на угол 180° и колебания выходной величины отстают от колебаний входной величины на половину периода. При проектировании САУ в обязательном порядке необходимо учитывать эти обстоятельства.