Визначення площ контакту і зближення
Для розрахунку фактичної площі контакту і зближення шорстку поверхню моделюють набором сферичних сегментів радіусу r, вершини яких розподілені по висоті таким чином, щоби відповідати опорній кривій реальної поверхні. Розглянемо контакт шорсткої поверхні з абсолютно гладкою твердою площиною, що суттєво спрощує задачу, а отримані залежності мають такий же вигляд, як і для контакту двох шорстких поверхонь.
Зв’язок між фактичною площею контакту і зближенням можна знайти за допомогою кривої опорної поверхні. Якщо шорстка поверхня зближується з гладкою, то Ap в залежності від зближення виражається з формули (3.3) у вигляді:
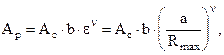 (3.19)
(3.19)

А фактична площа контакту відповідно рівна:
 (3.20)
(3.20)
де a - коефіцієнт, що враховує пружне осадження виступів і їх розплющування.
Як було показано вище, при пружному контакті a=1/2, при пластичному a=1.
При деякому нормальному навантаженні фактична площа контакту рівна сумі площ контакту 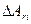 , утворених в результаті деформації окремих виступів, тобто
, утворених в результаті деформації окремих виступів, тобто
 (3.21)
(3.21)
Якщо деформація виступів пластична, то згідно рівняння (3.16) для фактичної площі контакту отримаємо наступний простий вираз:
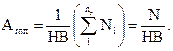 (3.22)
(3.22)
Підклавши  в формулу (3.20), знайдемо формулу для зближення при пластичному контакті:
в формулу (3.20), знайдемо формулу для зближення при пластичному контакті:
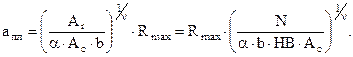 (3.23)
(3.23)
При пружній деформації виступів використаємо формулу Герца (3.24) і будемо сумувати площу контакту з врахуванням відмінностей в деформації виступів, обумовлених різницею їх висот.
Для пружного контакту згідно формулі Герца:
 (3.24)
(3.24)
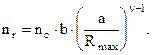 (3.25)
(3.25)
Тут nr – число контактуючих виступів при зближенні а;
nc – число всіх виступів по площі Ac.
Тоді фактична площа контакту знайдеться інтегруванням:
 (3.26)
(3.26)
В результаті інтегрування отримаємо:
 (3.27)
(3.27)
Тут  де
де  - гама функція (k1=1 при n=1, k1=0,8 приn=2 іk1=0,68 приn=3).
- гама функція (k1=1 при n=1, k1=0,8 приn=2 іk1=0,68 приn=3).
Значення зближення знайдемо з формули(3.20)при 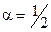 , тобто
, тобто
 (3.28)
(3.28)
Формули виведені для контакту шорсткої поверхні з гладкою. Можна показати, що при контакті двох шорстких поверхонь замість n, b, Rmax і r підставляють їх еквівалентні значення nS, bS, RmaxS і, rS які характеризують обидві контактуючі поверхні:
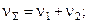 (3.29)
(3.29)
 (3.30)
(3.30)
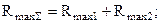 (3.31)
(3.31)
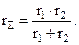 (3.32)
(3.32)
Тут 
В формулах індексами 1 і 2 позначені характеристики першої і другої контактуючої поверхонь. Коефіцієнт k2 в залежності від n1 і n2 приведені в таблиці 3.3.
Таблиця 3.3- Значення коефіцієнту k2
| n1/n2 | |||
| 0,5 | 0,33 | 0,25 | |
| 0,33 | 0,16 | 0,1 | |
| 0,25 | 0,1 | 0,05 |
Як видно з приведених формул, при пластичному контакті фактична площа залежить від навантаження лінійно, а при пружному – в степені 0,75…0,85. Зближення міняється в залежності від навантаження в степені 0,3…0,5. Приведені теоретичні залежності, достатньо точно відповідають експериментальним дослідженням.
Окремо зупинимося на формуванні ФПК гуми, оскільки вони широко використовуються у вузлах машин і механізмів і, особливо, в автотранспортних засобах. Гуми, незалежно від природи (на основі натуральних або штучних каучуків), мають надзвичайно низький модуль пружності (порядку 5-30 МПа). Коефіцієнт Пуассона в них близький до 0,5, отже, вже при невеликих тисках вони підпорядковуються закону Паскаля - тобто поводяться як рідини. На відміну від твердих тіл, уже при тиску порядку значення модуля пружності, фактична площа контакту в них наближається по величині до номінальної площі.
Розмір ФПК можна розрахувати по уточненій формулі Бартенєва Г.М. - Лаврентьєва В.В.:
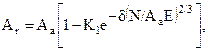 (3.33)
(3.33)
де - K1=0,8…1; d @ 1,2(ar/Rz)1/3; a = n0/nm, nm - число виступів у розрахунку на одиницю номінальної площі контакту; no - число виступів, пересічених середнім рівнем; Е - модуль пружності гуми.
Елементарні акти взаємодії поверхонь, що призводять до виникнення тертя і зносу, здійснюються, як вже зазначалос вище|, на плямах фактичного контакту. Число плям фактичного| контакту можна розрахувати по формулі
 (3.34)
(3.34)
де Кr — коефіцієнт, що враховує характер контакту виступів; для пружного контакту Кr=11, для пластичного Кr=21
pc/pr – відношення між контурним та фактичним тиском в парі тертя.
Середня площа  однієї плями контакту
однієї плями контакту
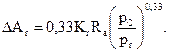 (3.35)
(3.35)
Середня відстань між плямами контакту Sr
 (3.36)
(3.36)
Від розміру плям контакту залежать розмір частинок зносу, час взаємодії на одиничному контакті і температура. Середня відстань між плямами фактичного контакту впливає на частоту взаємодії плям при терті.
Слід пам’ятати, що фактичний тиск рr на контакті дуже великий. Це часто приводить до пластичної деформації виступів. У ряді випадків в зоні контакту виникає повзучість, унаслідок чого характеристики контакту в часі можуть змінюватися при незмінності прикладеного зовнішнього. Ці так звані властивості реологій контакту особливо сильно виявляються з підвищенням температури в зоні контакту.
Наведені формули для розрахунку ФПК не враховують впливи часу дії навантаження і температури.
Дата добавления: 2015-10-19; просмотров: 1140;
