Контактна деформація виступів

Коли дві поверхні вступають в контакт виступи поверхонь під дією прикладеного навантаження N деформуються пружно і пластично. Спочатку має місце пружна деформація, тобто форма мікронерівності відновлюється повністю після зняття навантаження, а пізніше, при деякому значенні напруження, деформація стає пружно - пластичною, тобто форма нерівностей відновлюється тільки частково і залишається пластична деформація. Коли величина цієї деформації значно більше пружної, деформацію вважають пластичною. При цьому контакт поверхонь спряжених тіл залишається дискретним. Тому шорстке тіло можна моделювати набором виступів правильної геометричної форми. Найбільш повно відповідають реальній поверхні сферична, конусна, циліндрична (стрижнева) і еліпсовидна формі виступів.

Застосування моделей у вигляді набору стрижнів або конусів недоцільно, оскільки нормальні напруження на межі (для стрижневої моделі) і в центрі (для конусної моделі) контакту таких моделей є невизначеними і за їх допомогою не можна описати пружні деформації. Стрижнева модель передбачає також, що розмір контакту не залежить від навантаження, що не відповідає реальному контакту шорстких тіл. Таму найбільш доцільним вважається моделювання нерівностей поверхні набором сфер різного діаметру.

Якщо допустити, що форма виступу наближується до сферичної, то для розрахунку пружної деформації сфери можливе застосування формули Герца. Тоді, при контактуванні двох сфер радіусів r₁ і r₂ деформація а і площа контакту DAr будуть рівні (рисунок 3.11)

(3.11)

(3.12)

де E - приведений модуль пружності, що знаходиться з формули

(3.13)

де E₁, E₂ - модулі пружності,

m₁, m₂ - коефіцієнти Пуассона, а індекси 1 і 2 відносяться до першої і другої поверхонь відповідно;

r - приведений радіус, рівний

(3.14)

a - зближення або деформація пружних сфер

(3.15)

P_i - сила прикладена між двома сферичними виступами.

L - віддаль між центрами сфер.

Рисунок 3.11 – Контакт двох сфер

При пластичній деформації сферичного виступу або при занурюванні його в пластичний напівпростір площу і деформацію приблизно можна оцінити виходячи з того, що напруження на контакті рівні твердості, оскільки при визначенні твердості теж використовується занурення сферичного індентору. Тоді

(3.16)

де НВ - твердість по Брінелю.

. (3.17)

На рисунку 3.12 показаний контакт жорсткої сфери з пружним (рисунок 3.12, а) і пластичним(рисунок 3.12, б) напівпростором. Розрахунок по наведеним вище формулах показує, що при пластичному контакті площа перерізу DА_р приблизно рівна площі контакту DА_r, а при пружному: DА_r = 0,5DА_р. У загальному випадку:

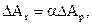(3.18 )

де a - коефіцієнт, який при пружному контакті a = 0,5, при пластичному a = 1, а при пружно-пластичному 0,5 < a < 1.

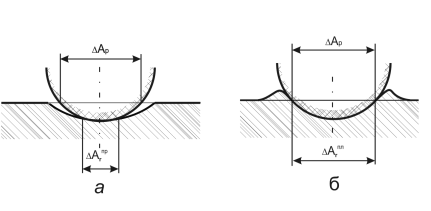
Рисунок 3.12 – Схема контакту жорсткої сфери з пружним (а) і пластичним (б) на півпростором