Імовірнісні характеристики параметрів профілю

Шорсткість робочої поверхні деталі залежить від великого числа різних факторів і їхнього поєднання. На якість поверхні впливають метод виготовлення і вид механічної обробки, фізико-механічні властивості матеріалу деталі, а в процесі роботи — експлуатаційні фактори. Більшість визначальних факторів і їхнє поєднання мають випадковий характер, тому процес формування робочої поверхні деталі також можна вважати випадковими. Параметри профілю розглядають як випадкові величини і при оцінці шорсткості поверхні використовують методи математичної статистики.

Основними статистичними характеристиками робочої поверхні деталі є: математичне очікування величини відхилень нерівностей від середньої лінії (чи висот нерівностей профілю), середнє квадратичне відхилення, кореляційна функція, спектральна щільність. Спряження двох деталей характеризується взаємною кореляційною функцією і взаємною спектральною щільністю.

У результаті статистичного аналізу профілів механічно оброблених металевих поверхонь встановлено, що розподілення висот нерівностей (рисунок 3.7), як правило, добре описується нормальним законом [9, 20]

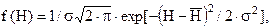(3.9)

де 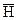- математичне очікування висоти нерівностей профілю,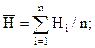

s-середнє квадратичне відхилення висоти,

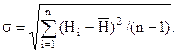
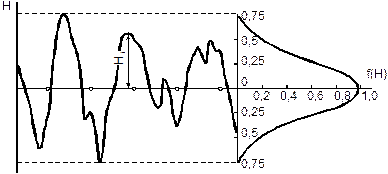Процес формування шорсткості відноситься до стаціонарних випадкових процесів. Стаціонарними називаються випадкові процеси, що протікають у часі приблизно однорідно, стабільно і, які мають вид безперервних випадкових коливань, відносно деякого середнього значення, причому ні середня амплітуда, ні характер цих коливань з часом не мають суттєвих змін. Стаціонарність — важлива властивість, що дозволяє в якості початку відрахунку прийняти будь-який момент часу. Стосовно до шорсткості це означає, що вимір висот нерівностей можна починати в будь-якій точці.

Статистично основними умовами стаціонарності випадкового процесу є: перше — незалежність його основних імовірнісних характеристик від аргументу (математичне очікування m (х) = const, дисперсія D (х) = const); друге — затухання (рисунок 3.8) нормованої кореляційної функції r (х) = K(х)/D®0 (тут K(х) — кореляційна функція).

Процес формування шорсткості робочої поверхні при деяких методах механічної обробки деталей має властивість ергодичності. Ергодичність процесу означає, що математичне очікування, отримане по одній реалізації, дорівнює математичному очікуванню, отриманому по множині реалізацій. При рішенні практичних задач це дозволяє визначати статистичні характеристики процесу на одній ділянці спостережень (по одній серії вимірів).

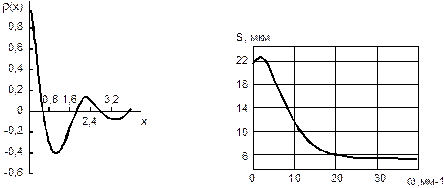
Рисунок 3.8 - Графік нормованої кореляційної функції стаціонарного випадкового процесу	Рисунок 3.9 - Спектральна щільність шорсткості шліфованої поверхні (Rа = 1,25…2,50 мкм)

Спектральна щільність являє собою щільність розподілу дисперсій параметра профілю по частотах безперервного спектру. Спектром називається функція, яка описує розподіл амплітуд по різних частотах. Спектр показує, якого роду коливання переважають у даному процесі; спектральна щільність S(w) (тут w— частота) виражається через кореляційну функцію K(х) випадкового процесу за допомогою інтеграла Фур'є

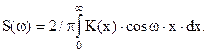(3.9)

Спектральна щільність може бути представлена графічно (рисунок 3.9). Замість спектральної щільності часто використовують нормовану спектральну щільність

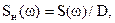(3.10)

де D—дисперсія випадкової функції.

При різних методах механічної обробки металічної поверхні деталі одержують профілі поверхні, що мають різні імовірнісні характеристики і напрямок нерівностей. На рисунку 3.10 показані щільності розподілу і автокореляційні функції, які характеризують шорсткість робочої поверхні деталі після відповідного методу механічної обробки.

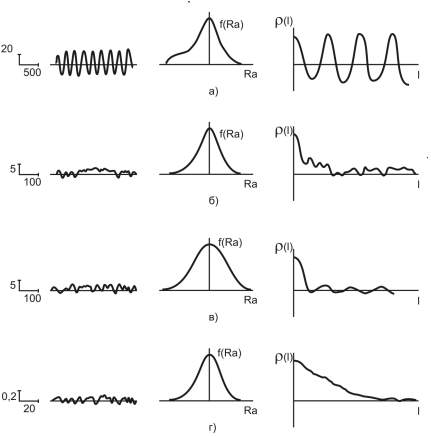
Рисунок 3.10 – Імовірнісні характеристики робочих поверхонь деталей при різних методах обробки: а – стуругання чистове; б – точіння чистове; в. – шліфування; г – суперфініш; I – вид профілю; II – вид функції щільності розподілу значень; III – вид нормованої автокореляційної функції