Квадратурные формулы
ОЛ-6, МП-13, ЭР-3, ЭР-4
Требуется вычислить приближенно интеграл
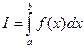
где f(x) − непрерывная на отрезке [a, b]функция.
Квадратурные формулы
В качестве приближенного значения интеграла I рассматривается число
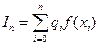 (1)
(1)
где f(xi) − значения функции f(x)в точках х = xi, i = 0, 1, ..., n, qi − числовые коэффициенты. Формула (1) называется квадратурной формулой. Точки xi называются узловыми точками или узлами квадратурной формулы, а числа qi − весовыми коэффициентами или весами квадратурной формулы. Разность
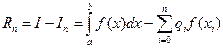
называется погрешностью квадратурной формулы. Погрешность зависит как от расположения узлов, так и от выбора весовых коэффициентов.
Говорят, что квадратурная формула точна для многочленов степени s, если при замене f(x)на произвольный алгебраический многочлен степени не выше s приближенное равенство 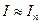 становится точным.
становится точным.
Если 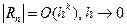 , то k − порядок точности (
, то k − порядок точности ( 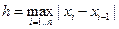 ).
).
Дата добавления: 2015-10-19; просмотров: 728;
