Шкала Мооса
| Материал | Баллы |
| Тальк | |
| Гипс | |
| Кальцит | |
| Флюорит | |
| Апатит | |
| Ортоклаз | |
| Кварц | |
| Топаз | |
| Корунд | |
| Алмаз |
Каждый последующий минерал оставляет царапину на предыдущем, т.е. это объективный метод измерения.
Результаты измерений, полученные попарным сопоставлением, можно уточнить методом последовательного приближения.
Влияние на результаты экспертизы состава экспертов
Тестирование. При формировании экспертной группы целесообразно провести тестирование, взаимооценку экспертов и проверку согласованностей мнений.
Тестирование состоит в решении экспертами задач, с известными организаторам тестирования, но неизвестными экспертам результатами, и проверке по критерию Фишера гипотезы о принадлежности оценок разных экспертов к одной и той же генеральной совокупности оценок.
Самооценка состоит в том, что каждый эксперт в ограниченное время отвечает на вопросы специально составленной анкеты. Такое испытание проводят на компьютере и затем получают балльную оценку. Эксперты могут оценивать и друг друга, но для этого необходима доверительная обстановка и опыт совместной работы.
Согласованность мнения экспертов можно оценивать по величине коэффициента конкордации:
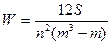
где S — сумма квадратов отклонений всех оценок рангов
каждого объекта экспертизы от среднего значения;
п — число экспертов;
т — число объектов экспертизы.
Коэффициента конкордации изменяется в диапазон  , причем 0 — полная несогласованность, 1 — полное единодушие.
, причем 0 — полная несогласованность, 1 — полное единодушие.
Пример.Необходимо определить степень согласованности мнения пяти экспертов, результаты ранжирования которыми семи объектов приведены в табл. 10.3.
Оцениваем среднеарифметическое число рангов:
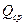 = (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
= (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
Затем оцениваем сумму квадратов отклонений от среднего: S=630. Определяем величину коэффициента конкордации:
W= 12 ´ 630 / 25´ (343 - 7) = 0,9.
Хороший результат! Мнения экспертов хорошо согласованы.
Влияние на результаты экспертизы количественного состава экспертов. С ростом числа экспертов в группе точность измерения повышается, что характерно для многократных измерений.
Количество экспертов n, обеспечивающее заданную точность измерений, можно установить, зная закон распределения мнений экспертов и максимально допустимую стандартную ошибку оценки Sх.
Тогда, используя известное выражение, можно определить минимальное количество экспертов п, обеспечивающее заданную точность измерения:
Таблица 10.3
Дата добавления: 2015-10-13; просмотров: 824;
