Данные для оценки согласованности мнений пяти экспертов
| Номер объекта экспертизы | Оценка эксперта | Сумма рангов | Отклонение от среднего | Квадрат отклонения | ||||
| 1 | 2 | 3 | 4 | 5 | ||||
| 6 | 4 | |||||||
| 2 | -5 | |||||||
| 6 | 6 | |||||||
| -13 | ||||||||
| 6 | ||||||||
| 1 |
,
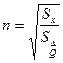где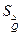 
— стандартное отклонение, которое определяют
по формуле:
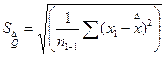
где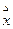 
среднеарифметическое значение оценок экспертов;
n1 — число оценок, дававшихся экспертами.
Различают также индивидуальное и коллективное мнение экспертов, последнее считают более точным, а главное, согласованным.
В роли экспертов могут выступать люди со специальной подготовкой, потенциальные потребители и изготовители продукции.
Причинно-следственные диаграммы Исикавы
Считается, что этот экспертный метод появился в Японии для выявления причин сбоя технологических процессов, когда очевидные его нарушения обнаружить трудно.
Существуют определенные правила построения таких диаграмм, которые определяют структуру показателей качества и значимость каждого фактора:
1. Используется группа работников, из которой руководство устраняется.
2. Сохраняется анонимность высказываний.
3. Младшие высказываются первыми.
4. Время проведения экспертизы ограниченно.
5. За найденное решение автор должен получить вознаграждение.
Допустим, нужно определить, от каких факторов и в какой мере зависит качество выпекания хлеба.
Вначале выделим общепринятые факторы, а именно: качество труда, качество документации, качество средств труда и качество предметов труда. Далее каждую составляющую разделим на причины и для каждой из них определим экспертным путем весовой показатель. Пример диаграммы приведен на рис. 10.1.
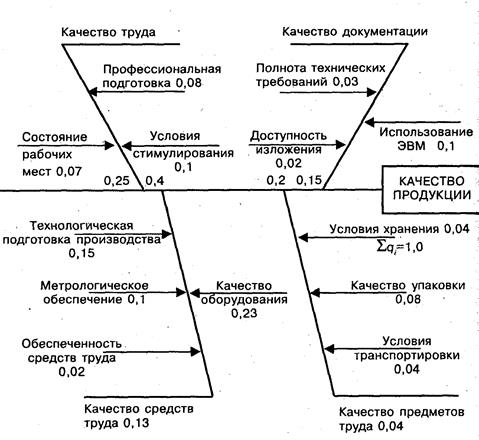
Рис. 10. 1. Пример диаграммы Исикавы
Часто диаграмму удобнее составлять «по ходу» технологического процесса. Рассмотрим, например, проявление пленки в какой-то фирме. Такой пример приведен на рис. 10. 2.
Аналитический метод определения весовых показателей
Этот метод используют, если выходная характеристика процесса описывается аналитической функцией, которая получена на основании теоретических предпосылок или экспериментальных данных.
Математической базой метода является использование полного дифференциала функции.
Пример.Необходимо определить весовые коэффициенты линейных размеров, влияющих на объемную погрешность цистерны.
1.Объем цилиндра определяется выражением:
,
где W — объем цилиндра,
D — диаметр,
l — длина,
p — число пи.
2. Определим полный дифференциал:
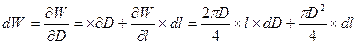
3. Принимая во внимание, что при малых отклонениях допустимо дифференциал заменить отклонением, получим:
;
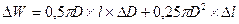где DW, DD, Dl — погрешности составляющих величин.
4. Допустим, что на чертеже цистерны указано, что D = 2,0 м и l= 3 м, а фактически измерено, что DФ = 1,95 м и lФ. = 2,96 м. Тогда можно вычислить абсолютные погрешности, затем, относительную погрешность:
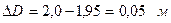
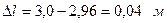
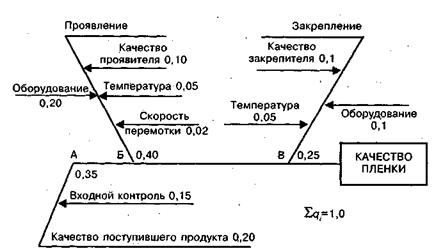
Рис. 10. 2. Диаграмма Исикавы, составленная «по ходу» технологического процесса
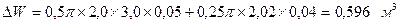
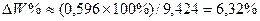
Можно решить и обратную задачу. Зная DW назначить DD и Dl т.е., допуски на эти размеры
, 
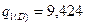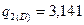
Потребительский и производственный допуски
Для гарантированного обеспечения качества в производстве обычно руководствуются более жесткими требованиями к показателям качества по сравнению с требованиями к показателям качества продукции, предлагаемой рынку. Чаще всего это выражается в том, что уменьшают допустимые отклонения характеристик продукции установленных разработчиком.
Различают, таким образом, потребительский допуск и производственный допуск, разница между которыми и является запасом. Соотношение производственного и потребительского допусков можно представить в виде диаграммы, показанной на рис.10. 3.
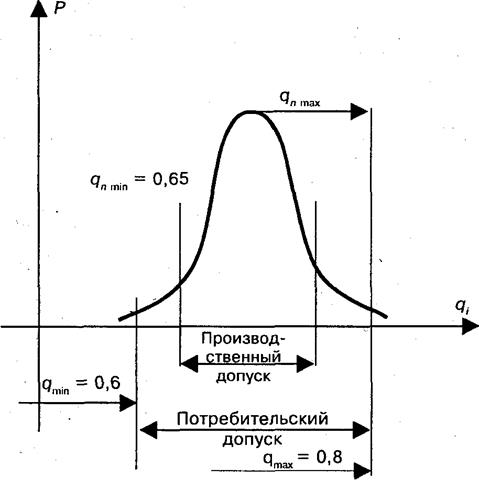
Рис. 10. 3. Соотношение производственного и потребительского допусков на диаграмме распределения показателя качества
Дата добавления: 2015-10-13; просмотров: 1449;