Размах вариации. Среднее линейное отклонение
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два ряда распределения, имеющие одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблености (вариации) величины изучаемого признака. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Например, заработная плата трех рабочих равна соответственно 408, 404, 406. Ясно, что средняя заработная плата 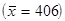 будет достаточно полно характеризовать всю совокупность. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Например, заработная плата трех рабочих: 408, 1200, 2600. Средняя будет нетипична для данной совокупности –
будет достаточно полно характеризовать всю совокупность. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Например, заработная плата трех рабочих: 408, 1200, 2600. Средняя будет нетипична для данной совокупности –

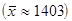
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц к средней измеряется рядом абсолютных, средних и относительных показателей.
К таким показателям относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации - это разность между наибольшим (Хmak) и наименьшим (Хmin) значениями вариантов: R= Хmaх-Xmin
Таблица 4.1.
Группы предприятий по объему товарооборота, тыс.руб. 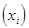
| Число предприятий
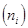
|
| 90 – 100 | |
| 100 – 110 | |
| 110 – 120 | |
| 120 – 130 | |
| Итого |
Определяем показатель размаха вариации:
R = 130 - 90 = 40 тыс.руб.
Безусловным достоинством этого показателя является простота расчета. Однако, размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничены достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.
Точнее характеризует вариацию признака показатель, основанный на учете колеблености всех значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений признака отдельных единиц совокупности от этой величины. К таким показателям относятся среднее линейной отклонение, дисперсия и среднее квадратичное отклонение, представляющее собой среднюю арифметическую из отклонений индивидуальных значений признака от средней арифметической. Среднее линейное отклонение рассчитывается из отклонений в первой степени, дисперсия и среднее квадратическое - из отклонений второй степени. Так как алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической (согласно первому свойству) всегда равна нулю, то для расчета среднего линейного отклонения используется арифметическая сумма отклонений, т.е. суммируются абсолютные значения индивидуальных отклонений значений признака независимо от знака.
Среднее линейное отклонение d вычисляется по следующим формулам:
· для несгруппированных данных (среднее линейное отклонение простое):
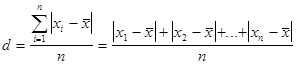
Порядок расчета среднего линейного отклонения следующий:
1. по значениям признака исчисляется средняя арифметическая:
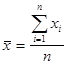
2. определяются отклонения каждой варианты Xi от средней
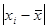
3. рассчитывается сумма абсолютных величин отклонений:
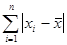
4. сумма абсолютных величин отклонений делится на число значений:
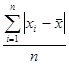
· для сгруппированных данных (среднее линейное отклонение взвешенное):
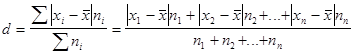
Порядок расчета среднего линейного отклонения взвешенного следующий:
1. вычисляется средняя арифметическая взвешенная:
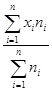
2. определяются абсолютные отклонения вариант от средней
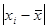
3. полученные отклонения умножаются на частоты
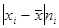
4. находится сумма взвешенных отклонений без учета знака:
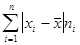
5. сумма взвешенных отклонений делится на сумму частот:
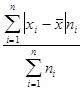
Дата добавления: 2015-09-02; просмотров: 3344;
