Выборочное среднее квадратическое отклонение.
Определение. Арифметическое значение квадратного корня из выборочной дисперсии называется выборочным средним квадратическим отклонением:
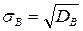 (10)
(10)
Исправленное выборочное среднее квадратическое отклонение
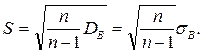 (11)
(11)
4. Мода.Определение. Модой М0 называют значение признака, которое имеет наибольшую частоту (ni = max).
Например, для распределения, данного табл. 5, мода равна 5.
5. Медиана. Медианой те называют значение признака, которое делит статистическое распределение на две равные части:
me = xk+1, если n = 2k+1,
me = 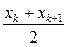 , если n=2k
, если n=2k
6. Коэффициент вариации. Для сравнивания меры рассеяния значений признаков около выборочной средней в разных выборках служит коэффициент вариации.
Определение. Коэффициентом вариации V называется отношение выборочного среднего квадратического отклонения к выборочной средней, выраженное в процентах:
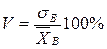 (12)
(12)
Пусть изучается случайная величина X. Из генеральной совокупности сделана выборка объема п со значениями признака х1 х2,..., хn. Предположим, что х1, х2,...,хn различны. Их можно рассматривать как случайные величины Х1, Х2, ..., Хn, имеющие то же распределение, что и случайная величина X, и, следовательно, одинаковые значения М(Х)иD(Х). Тогда
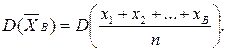
Воспользовавшись свойствами дисперсии находим
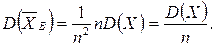
Пусть σ 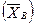 – средняя квадратическая ошибка выборочной средней. Тогда
– средняя квадратическая ошибка выборочной средней. Тогда
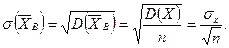
Вывод. Средняя квадратическая ошибка выборочной средней σ( 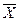 B)в
B)в 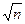 раз меньше среднего квадратического отклонения случайной величины X, возможные значения которой попали в выборочную совокупность.
раз меньше среднего квадратического отклонения случайной величины X, возможные значения которой попали в выборочную совокупность.
Дата добавления: 2015-09-21; просмотров: 2265;
