ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ.
ЛЕКЦИЯ 5
Вектором называется направленный отрезок 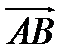 с началом в точке А и концом в точке В (который можно перемещать параллельно самому себе).
с началом в точке А и концом в точке В (который можно перемещать параллельно самому себе).
| А |
| В |
Длиной (или модулем) вектора 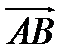 называется число
называется число 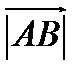 , равное длине отрезка
, равное длине отрезка 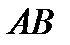 .
.
Векторы, лежащие на одной или на параллельных прямых, называются коллинеарными.
Если начало и конец вектора совпадают, например 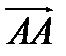 , то вектор называется нулевым и обозначается
, то вектор называется нулевым и обозначается 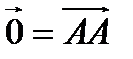 .
.
Длина нулевого вектора равна нулю: 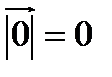 . Считаем, что нулевой вектор коллинеарен любому вектору.
. Считаем, что нулевой вектор коллинеарен любому вектору.
Действия с векторами:
1. Произведение вектора 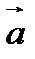 на число
на число 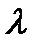 называется вектор
называется вектор 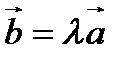 , имеющий длину
, имеющий длину 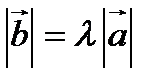 , направление которого совпадает с направлением
, направление которого совпадает с направлением 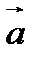 , если
, если 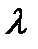 >0, и противоположно ему, если
>0, и противоположно ему, если 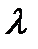 <0.
<0.
2. Суммой двух векторов 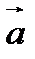 и
и 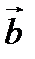 называется вектор
называется вектор 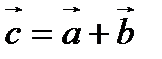 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 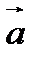 , а конец совпадает с концом вектора
, а конец совпадает с концом вектора 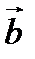 при условии, что начало вектора
при условии, что начало вектора 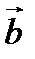 совпадает с концом вектора
совпадает с концом вектора 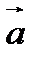 (правило треугольника).
(правило треугольника).
| а |
| в |
| с |
В этом случае вектор 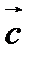 является диагональю параллелограмма
является диагональю параллелограмма
(правило параллелограмма).
3. Скалярным произведением двух векторов определяется равенством: 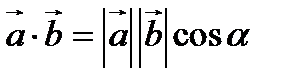 где
где 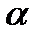 - угол между векторами
- угол между векторами 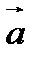 и
и 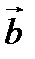 .
.
4. Проекцией вектора 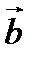 на вектор
на вектор 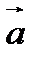 называется число
называется число 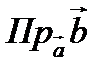 , равное длине вектора
, равное длине вектора 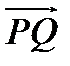 , если векторы
, если векторы 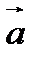 и
и 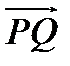 одинаково направлены, и равное длине вектора
одинаково направлены, и равное длине вектора 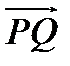 со знаком «-», если векторы
со знаком «-», если векторы 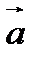 и
и 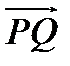 направлены в разные стороны. Проекция находится по формуле:
направлены в разные стороны. Проекция находится по формуле: 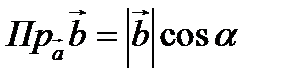
Следствие: 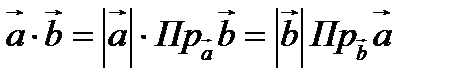 .
.
| P |
| Q |
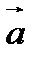
|
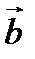
|
Проекция суммы двух векторов равна сумме проекций:
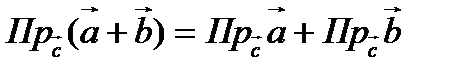
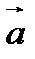
|
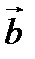
|
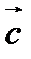
|
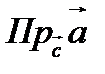
|
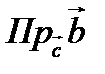
|
Дата добавления: 2015-10-13; просмотров: 711;
