Энергетические диаграммы уединенного атома и твердых тел

Необходимо прежде всего вспомнить о том, что не всегда можно рассматривать электрон только как некоторую частицу, обладающую определенным отрицательным зарядом.

В ряде случаев такое предположение оказывается достаточным. Так, например, рассматривая закон движения электрона, помещенного в электрическое или магнитное поле, мы убеждаемся, что электрон, подчиняется общим законам динамики движения частиц.

В то же время, если поток электронов взаимодействует с решеткой, параметры которой соизмеримы с атомными размерами, то в этом случае проявляются волновые свойства электрона. Мы наблюдаем характерное для волнового процесса явление дифракции. Таким образом, электрон следует характеризовать не только параметрами, свойственными частицам (масса, скорость, ускорение), но и параметрами волнового процесса (длина волны).

Если рассматривать электроны в атоме как элементарные заряженные частицы, вращающиеся вокруг атомного ядра по некоторым замкнутым орбитам, то мы должны предположить, что на электрон при этом действуют две силы: центробежная, определяемая радиусом орбиты и скоростью движения, и центростремительная, определяемая силами электростатического взаимодействия ядра и электрона. Нормально эти две силы должны уравновешивать друг друга:

(1.1)

Здесь

т—масса электрона,

r—радиус орбиты,

v—скорость движения электрона,

q—заряд электрона,

ε — относительная диэлектрическая проницаемость среды,

ε₀ —абсолютная диэлектрическая проницаемость свободного пространства.

Однако электрон, движущийся по замкнутой орбите, должен был бы излучать электромагнитную энергию. Энергия электрона при этом уменьшалась бы, и, в конце концов, электрон, потерявший свою энергию, был бы притянут ядром. В то же время имеются устойчивые орбиты, на которых электроны могут находиться сколь угодно долго. Это можно объяснить, только предположив, что при движении электрона по орбите образуется стоячая волна, и энергия при этом не излучается. Такое состояние может иметь место в том случае, когда на длине орбиты укладывается целое число длин волн.

Длина волны для электрона, движущегося со скоростью v, будет равна

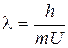
(1.2)

Это соотношение можно получить, приравнивая выражения, полученные для импульса электрона, исходя из его волновой и корпускулярной природы:

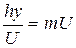
(1.3)

где h — постоянная Планка, v — частота.

Таким образом, для получения стоячей волны необходимо выполнение условия

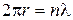
(1.4)

где п=1, 2, 3, 4, ...—любое целое число.

Исходя из этого и пользуясь соотношением (1.1), нетрудно получить в общем виде выражение для радиуса устойчивой орбиты

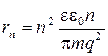
(1.5)

Отметим, что радиусы устойчивых орбит возрастают пропорционально квадрату числа п, называемого главным квантовым числом.

Полная энергия электрона, находящегося на орбите, складывается из его кинетической и потенциальной энергии:

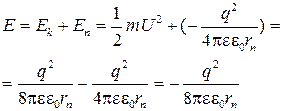(1.6 )

Подставляя (1.5) в (1.6), получаем

E=-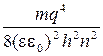

(1.7)

Таким образом, электрон может иметь некоторые конкретные значения энергии, определяемые главным квантовым числом п. Знак «минус» показывает, что энергия уменьшается с уменьшением радиуса орбиты. Минимальной энергией будет обладать электрон, расположенный на минимальной орбите

(п = 1). По мере увеличения главного квантового числа n разрешенные уровни энергии располагаются все ближе и ближе друг к другу, образуя непрерывный спектр при п → ∞, рис.1.2Практически удобнее за начало отсчета (E = 0) принимать минимальное значение энергии, соответствующее самой ближней к атомному ядру орбите, и считать, что энергия электрона увеличивается по мере увеличения радиуса орбиты. Такой прием обеспечивает гораздо большую наглядность последующего изложения. Все сказанное выше опиралось на представление о круговых орбитах электрона, лежащих в одной плоскости. Не рассматривалось и вращение электрона вокруг собственной оси (спин электрона).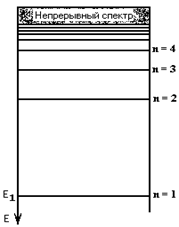

Рис.1.2. Энергетический спектр устойчивых орбит

В общем случае следует предположить, что — электроны движутся по эллиптическим орбитам (частным случаем при этом является круговая орбита). Ядро атома находится в одном из фокусов эллипса.

Круговая орбита характеризуется только ее радиусом. Эллиптическая орбита будет характеризоваться двумя величинами: малой и большой осями эллипса. В этом случае задать орбиту электрона, пользуясь только одной величиной, главным квантовым числом п, не удается, поэтому вводят орбитальное квантовое число l, которое также является целым положительным числом и может иметь для одного и того же значения п значения от нуля до (п – 1) : l = 0, 1, 2, . . ., (п — 1). Допуская, что электрон может вращаться вокруг оси, перпендикулярной плоскости орбиты, получаем, что электрон следует характеризовать еще спиновым квантовым числом. Если теперь перейти от двумерной (плоскостной) модели атома к трехмерной (объемной), то для определения положения орбиты и спина электрона в пространстве придется ввести еще два квантовых числа: орбитальное магнитное квантовое число и спиновое магнитное квантовое число. Так как спиновое квантовое число имеет всегда одно и то же значение s = ½, то для полного описания движения электрона в трехмерной модели атома требуется задать комбинацию из четырех квантовых чисел:

1. Главное квантовое числоп = 1, 2, 3,... , ∞, определяющее большую ось эллиптической орбиты. Этим определяется основной энергетический уровень или электронная оболочка.

2. Орбитальное квантовое число l ==0, 1, 2, . . ., (п—1), определяющее малую ось эллиптической орбиты. Для данного n в зависимости от величины l оболочка разделяется на подгруппы. В каждой оболочке, носящей порядковый номер п, будет п подгрупп, определяемых значениями l от 0 до (n — 1).

3. Орбитальное магнитное квантовое число m_l = 0, ±1; ±2, . . ., ±l. Этим числом определяется ориентация эллиптической орбиты в пространстве. В каждой подгруппе будет, таким образом, (2l + 1) по-разному ориентированных орбит.

4. Спиновое магнитное квантовое число m_s = ±½, определяющее ориентацию вектора спина электрона.

Согласно принципу запрета, сформулированному в 1925 г. Паули, никакие два электрона в атоме не могут иметь одних и тех же значений этих четырех квантовых чисел. Так как первые три квантовых числа определяют форму, размеры и положение орбиты в пространстве, а для данной орбиты будет характерен определенный энергетический уровень, то отсюда следует, что в атоме может быть не более двух электронов, занимающих один и тот же энергетический уровень (определяемый первыми тремя квантовыми числами). Эти два электрона должны иметь взаимно противоположные спины, т. е. отличаться спиновым магнитным квантовым числом.

Так как оболочки, расположенные ближе к атомному ядру, характеризуются меньшей энергией электрона по сравнению с более удаленными, то отсюда следует, что электроны, стремясь занять уровни с минимальной энергией, будут заполнять внутренние оболочки до предела. Частично заполненной может быть только внешняя, наиболее удаленная от атомного ядра, оболочка.

При дальнейшем изложении можно ограничиться лишь двумя квантовыми числами п и l, считая, что в каждой подгруппе возможное количество электронов определяется величиной 2·(2l + 1), в которой учитываются магнитные квантовые числа. С учетом вышеизложенного энергетический спектр электронов в атоме несколько изменится и примет вид, представленный на рис. 1.3. На этой диаграмме дано общепринятое обозначение уровней, в котором цифровые значения l заменены буквенными обозначениями:	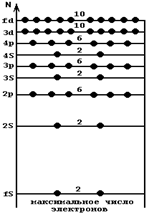Рис.1.3. Распределение электронов в атоме по энергетическому закону
l
Буква	s	p	d	f	g	h
Число электронов

Так, например, энергетический уровень, соответствующий п = 2 и l =0, обозначается символом 2s; п = 3, l == 2 — символом 3d и т. д.

Делаем заключение, что каждый отдельно взятый атом вещества может быть охарактеризован некоторым энергетическим спектром. Спектры для атомов одного и того же вещества будут идентичны. Можно было бы предположить, что при рассмотрении некоторой совокупности атомов следует пользоваться спектром одиночного атома, увеличивая число электронов, находящихся на том или ином уровне, во столько раз, сколько однотипных атомов включает в себя рассматриваемая система.

Однако такое допущение может быть принято только тогда, когда расстояния между атомами настолько велики, что мы можем пренебрегать взаимным влиянием атомов и считать, что принцип Паули выполняется для каждого атома в отдельности.

Если мы будем сближать атомы, то начиная с некоторого расстояния взаимное влияние атомов становится ощутимым, принцип Паули следует распространить на всю совокупность атомов в целом и линии спектра начнут расщепляться в группу уровней — зону. Взаимное влияние атомов в первую очередь начинает сказываться на внешней оболочке.

На внутренних оболочках взаимное влияние атомов сказывается меньше, и по мере приближения к атомному ядру расщепление уровня дает все более и более узкие зоны, вырождаясь постепенно в единый уровень, как это имело место для всех уровней одиночных атомов. Зоны будут состоять из уровней, появившихся в результате расщепления. Внутренние электронные оболочки атомов являются заполненными. Это значит, что все возможные состояния в них заняты электронами. Естественно, что и зоны, образовавшиеся за счет расщепления уровней, относящихся к внутренним оболочкам, являются заполненными зонами. Все уровни, образующие эту зону, заняты максимально допустимым количеством электронов.

Между зонами, объединяющими группу разрешенных для электронов энергетических уровней, расположены зоны значений энергии, которыми не могут обладать электроны. Так как в этих зонах нет уровней энергии, разрешенных для электронов, эти зоны называются запрещенными. Так, линейчатый энергетический спектр одиночного атома в твердом теле превращается в зонный спектр, в котором разрешенные зоны уровней разделяются запрещенными зонами.

На рис. 1.4 показан пример расщепления уровней в зоны для лития и бериллия. Так как расстояние между атомами в твердом теле не является произвольным, а имеет вполне определенную для данного вещества величину d₀, то естественно рассматривать структуру зон именно для этого расстояния между атомами.

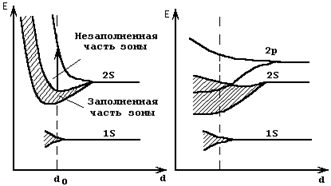
а) б)

Рис.1.4. Расщепление энергетических уровней атома в зоны при

взаимодействии атомов в твердом теле:

а) для лития, б) для бериллия.

Каждый атом лития (рис. 1.4, а) имеет полностью заполненный уровень 1s (два электрона) и частично заполненный уровень 2s (один электрон). При расщеплении этих уровней в зоны образовалась одна полностью заполненная зона (нижняя) и одна частично заполненная зона (верхняя), имеющая по одному свободному уровню на каждый находящийся в рассматриваемом объеме атом.

Переход электронов из одной зоны в другую будет возможен, если электрон получит дополнительную энергию, превышающую ширину запрещенной зоны, разделяющей эти две разрешенные зоны. Внутри верхней зоны электроны могут переходить с занятых уровней на свободные за счет получения значительно меньших количеств энергии.

Для атома бериллия (рис. 1.4, б) два верхних уровня при расщеплении дали перекрывающиеся зоны. Так как атом бериллия имеет 4 электрона, то уровни 1s и 2s у него заняты полностью. Тем не менее верхняя зона, образовавшаяся в результате перекрытия зон 2s и 2р, имеет большое количество свободных уровней (по 6 на каждый атом), которые могут заниматься электронами, находящимися в этой зоне. Это значит, что электроны, находящиеся в частично заполненной зоне, могут изменять свою энергию в достаточно широких пределах.

Таким образом можно подвести итог:

1) в уединенном атоме электроны, вращающиеся вокруг ядра, обладают энергией, которая тем больше, чем больше радиус орбиты;

2) допустимые значения энергии электронов в атоме дискретны, т.е. электроны могут двигаться не по любым, а только по определенным орбитам – разрешенным, каждой из которых соответствует вполне определенная энергия электрона. Возможные значения этой энергии называются разрешенными энергетическими уровнями. На каждом энергетическом уровне может находиться не более 2-х электронов (с разными направлениями спинов);

3) электроны могут переходить с одного энергетического уровня на другой, если этот уровень свободен.

4) в твердом теле в результате взаимодействия атомов каждый из возможных энергетических уровней уединенного атома расщепляется, образуя зоны уровней. Из разрешенных энергетических уровней образуются разрешенные энергетические зоны. Этих зон столько, сколько разрешенных энергетических уровней в атоме.

5) разрешенные зоны отделены друг от друга промежутками – запрещенными зонами, где электроны находиться не могут.

На некотором расстоянии от верха валентной зоны должна существовать полностью свободная зона. Эта зона отделена от валентной запрещенной зоной, имеющей некоторую ширину ΔЕ (рис. 1.5). Мы уже говорили о том, что при сообщении кристаллу некоторого количества энергии отдельные электроны могут покинуть ковалентные связи и превратиться в свободные носители заряда. В зонной модели это значит, что некоторому электрону, находящемуся в валентной зоне, сообщено количество энергии, превышающее величину ΔЕ.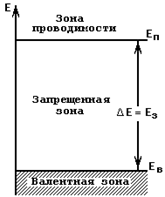

Рис.1.5.Зонная энергетическая диаграмма для внешних (валентных) электронов

Такой электрон окажется переброшенным из валентной зоны в верхнюю незаполненную зону, имеющую большое количество свободных уровней. В этой зоне электрон приобретает возможность изменять свою энергию под действием сил электрического поля, т. е. в этой зоне электрон становится свободным носителем заряда, электроном электропроводности. Поэтому такая зона получила название зоны проводимости.