Структура полупроводников

Кристаллическая решетка. Независимо от природы сил, возникающих при сближении частиц, общий характер их остается одинаковым (рис. 1.7, а): на относи­тельно больших расстояниях появляются силы притяжения Fп, быст­ро увеличивающиеся с уменьшением расстояния r между частицами (кривая 1), на малых расстояниях возникают силы отталкивания Fот, которые с уменьшением r увеличиваются значительно быстрее, чем Fп (кривая 2). На расстоянии r=r0 силы отталкивания уравновеши­вают силы притяжения и результирующая сила взаимодействия F обращается в нуль (кривая 3), а энергия взаимодействия достигает минимального значения U (рис. 1.7, б).   Поэтому состояние частиц, сближенных на расстояние r0, является состоянием устойчивого рав­новесия, вследствие чего частицы, предоставленные самим себе, должны выстраиваться в строгом порядке на расстоянии r0 друг от друга, об­разуя тело с правильной внутренней структурой — кристалл.

Рис.1.7.

Такая структура будет сохраняться до тех пор, пока энергия связи остается выше по абсолютному значению энергии теплового движения частиц. Частицы кри­сталла не могут свободно покидать свои положения равновесия, так как при удале­нии от этих положений энергия частиц уве­личивается и появляются силы, стремя­щиеся вернуть их в положения равновесия. Частицы как бы закреплены в положе­ниях равновесия. Единственной доступной формой движения для них является беспо­рядочное колебание около положений рав­новесия.

Для описания правильной внутрен­ней структуры кристаллов удобно поль­зоваться понятием кристаллической ре­шетки. Различают трансляционные решет­ки Бравэ и решетки с базисом.

Решетки Бравэ. С геометрической точ­ки зрения, правильное периодически пов­торяющееся размещение частиц в кристал­ле можно описать с помощью операции па­раллельного перемещения, или трансляции. На рис. 1.8,а показана решетка, полу­ченная трансляцией частицы вдоль трех осей: ОХ на отрезки а, 2а, За, .... ma, ОУ на отрезки b, 2b, Зb, .... nb, ...; OZ на от­резки с, 2с, 3с,.... рс, (m,n,p—целые числа). Положение любой частицы в та­кой решетке определяется вектором

(1.8)

Векторы, а, b, с называются наименьшими векторами трансляции, а численные их величины — периодами трансляции.

Решетка, построенная путем параллельного переноса (трансляции) какого-либо узла по трем направлениям, называется трансляционной решеткой, или решеткой Бравэ

Наименьший параллелепипед, пост­роенный на векторах а,b,с, называют элементарной ячейкой кристалла (рис. 1.8,б). Все элементарные ячейки, составляющие решетку, имеют одинаковые форму и объем. Во всех вершинах ячеек распола­гаются одинаковые атомы или группы атомов. Поэтому все вершины ячеек эквивалентны друг другу. Их называют узлами решетки. Для характеристики элементарной ячейки необходимо задать в общем случае шесть величин: три ребра ячейки (а, b, с) и три угла между ними 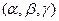. Эти величины называются параметрами элементар­ной ячейки.

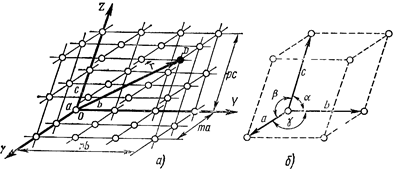
Рис.1.8.

За единицу измерения длины в решетках прини­мается не метр, а отрезки а, Ь, с. Их называют осевыми единицами.

Элементарные ячейки, содержащие частицы только в вершинах, называют простыми, или примитивными. На каждую такую ячейку приходится одна частица.

В ряде случаев для достижения более полного выражения симмет­рии решетки элементарные ячейки строят таким образом, что они со­держат частицы не только в вершинах, но и в других точках. Такие ячейки называют сложными. Наиболее распространенными из них являются (рис.19):

а)-базоцентрированные (БЦ), б)-объемноцентрированные (ОЦ), в)-гранецентрированные (ГЦ).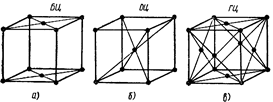

Рис.1.9

Решетки с базисом. Не всякую решетку можно получить трансля­цией одного узла.

Решетку общего типа называют решет­кой с базисом. Ее можно построить с по­мощью тех же трансляций, что и каждую из составляющих решеток Бравэ, только при этом надо транслировать не один узел, а не­сколько узлов — базис, задаваемый совокуп­ностью базисных векторов.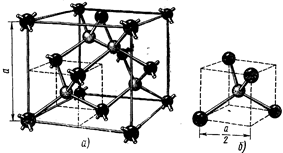

Рис.1.10

В каче­стве примера трехмерной решетки с базисом на рис.1.10,а показа­на решетка алмаза. Ее можно образовать двумя вставленными одна в другую ГЦ-решетками, смещенными по пространственной диагона­ли на 1/4 диагонали.

На рис. 1.10,б приведена элементарная ячей­ка решетки алмаза, выделенная на рис. 1.10,а пунктиром.

Индексы узлов (индексы Миллера узлов). Положение любого узла решетки относительно выбранного начала координат определяется заданием трех его координат (рис.1.11): х, у, z. Эти координаты можно выразить следующим образом:

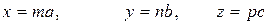(1.9)

где а, b, с — параметры решетки; m,n,p — целые числа.

Если за единицу измерения длин вдоль осей решетки принять параметры решетки, то координатами узла будут просто числа m,n,p. Эти числа называются индексами узла и записываются так: [[mnp]]. Для от­рицательного индекса знак минус ста­вится над индексом.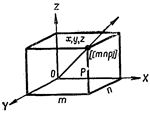

Рис.1.11

Например, для узла с координатами х = —2а, у = —1b, z=3с индексы записывают в следующем виде: .

Индексы направления (индексы Миллера направления). Для опи­сания направления в кристалле выби­рается прямая, проходящая через нача­ло координат. Ее положение однознач­но определяется индексами [[mnp]] первого узла, через который она проходит (рис. 1.11).

Индексы направления обозначают так: [mnp].

Индексы направления пред­ставляют собой три наименьших целых числа, характеризующих поло­жение ближайшего узла, лежащего на данном направлении.

Так, ин­дексами направления, проходящего через качало координат и узел [[435]], являются [435].

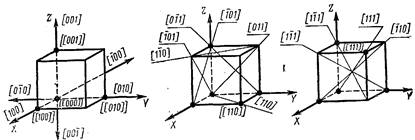
Рис.1.12

Кристаллографические плоскости (индексы Миллера плоскости). Положение кристаллографической плоскости определяется заданием трех отрезков А, В, С, которые она отсекает на осях решетки.

Выражают отрезки А, В, С в осевых единицах и записывают ве­личины, обратные этим отрезкам: 1/А, 1/В, 1/С. Полученные дроби приводят к общему знаменателю. Пусть таковым будет число D. Целые числа h=D/A, k=D/B, l=D/C и являются индексами плоскости. Они записываются так: (hkl).

Определим, например, индексы плоскости, отсекающей на осях отрезки А =1/2, Б=2, С= 1/3.

Отношения

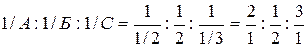
Общий знаменатель D = 2. Индексами плоскости являются:

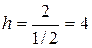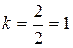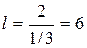, , . Плоскость обозначают (416).

На рис. 2,а показаны кристаллографические плоскости и соответствующие им индексы Миллера. Цифра 1 означает, что соответствующая плоскость проходит через точку соответствующей оси с единичной координатой. Цифра 0 означает, что кристаллографическая плоскость параллельна данной оси координат.

На рис. 1.13 показаны кристаллографические плоскости и соответствующие им индексы Миллера применительно к простейшей кубической решетке. Цифра 1 означает, что соответствующая плоскость проходит через точку соответствующей оси с единичной координатой. Цифра 0 означает, что кристаллографическая плоскость параллельна данной оси координат.

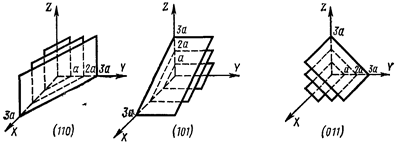
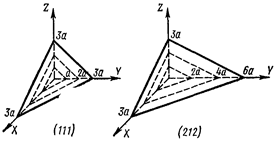
Рис.1.13

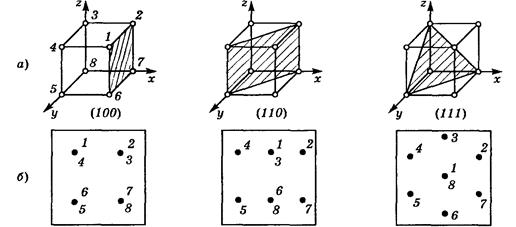
Рис. 1.14.

а — кристаллографические плоскости:

б — расположение атомов в кристаллографических плоскостях

Каждой кристаллографической плоскости свойственна своя плотность атомов на единицу площади. Например, если «посмотреть» на кристалл с кубической решеткой перпендикулярно плоскостям (100), (110) и (111), то расположение атомов в поле зрения будет таким, как показано на рис. 1.14, б (для ясности узловые атомы пронумерованы). Наибольшая плотность атомов соответствует плоскости (111), наименьшая — плоскости (100). У кремния плоскость (111) является плоскостью спайности: по ней, как правило, распространяются трещины, и происходит раскалывание кристалла.

Для разных кристаллографических плоскостей оказываются разными многие свойства и параметры кристалла: оптически свойства, скорость травления и др. Поэтому пластины для изготовления ИС шлифуют точно по заранее заданной кристаллографической плоскости.