Показатели тесноты связи между качественными признаками
Метод корреляционных таблиц применим не только к количественным, но и к описательным (качественным) признакам, взаимосвязи между которыми часто приходится изучать при проведении различных социологических исследований путем опросов или анкетирования. В этом случае такие таблицы называют таблицами сопряженности. Они могут иметь различную размерность. Простейшая размерность – 2х2 (таблица «четырех полей»), когда по альтернативному признаку («да» – «нет», «хорошо» – «плохо» и т.д.) выделяются 2 группы. В таблице 8 приведены условные данные о распределении 500 опрошенных человек по двум показателям: наличие (отсутствии) у них прививки против гриппа и факт заболевания (незаболевания) гриппом во время его эпидемии.
Таблица 8. Распределение 500 опрошенных человек
| Группа лиц | Число лиц | ||
| заболевших гриппом | не заболевших гриппом | Итого | |
| Сделавших прививку | 30 (а) | 270 (b) | |
| Не сделавших прививку | 120 (c) | 80 (d) | |
| Итого |
Нетрудно заметить, что среди сделавших прививку подавляющее большинство (270 из 300, или 90%) не заболели гриппом, а среди не сделавших большая часть заболела (120 из 200, или 60%). Таким образом, можно предположить, что прививка положительно влияет на предупреждение заболевания; другими словами, можно предположить, что распределение в таблице (a, b, c, d) не случайно и существует стохастическая зависимость между группировочными признаками. Однако выводы о зависимости, сделанные «на глаз», часто могут быть ненадежными (ошибочными), поэтому они должны подкрепляться определенными статистическими критериями, например критерием Пирсона χ2. Он позволяет судить о случайности (или неслучайности) распределения в таблицах взаимной сопряженности, а следовательно, и об отсутствии или наличии зависимости между признаками группировки в таблице. Чтобы воспользоваться критерием Пирсона χ2, в таблице взаимной сопряженности наряду с эмпирическими частотами записывают теоретические частоты, рассчитываемые исходя из предположения, что распределение внутри таблицы случайно и, следовательно, зависимость между признаками группировки отсутствует. То есть считается, что распределение частот в каждой строке (столбце) таблицы пропорционально распределению частот в итоговой строке (столбце). Поэтому теоретические частоты по строкам (столбцам) рассчитывают пропорционально распределению единиц в итоговой строке (столбце).
Так, в нашем примере в итоговой строке число заболевших 150 из 500, т.е. их доля – 30%, а доля не заболевших – 70%. Следовательно, теоретические частоты в первой строке для заболевших составят 30% от 300, т.е. 0,3*300=90, а для не заболевших – 0,7*300=210. По второй строке произведем аналогичные расчеты и их результаты занесем в таблицу в скобках.
Таблица 9. Эмпирические и теоретические частоты
| Группа | I (да) | II (нет) | ∑ |
| I (да) | 30 (90) | 270 (210) | |
| II (нет) | 120 (60) | 80 (140) | |
| ∑ |
На сопоставлении эмпирических и теоретических частот и основан критерий Пирсона χ2, рассчитываемый по формуле:
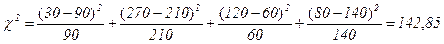 .
.
Рассчитанное (фактическое) значение χ2 сопоставляют с табличным (критическом), определяемым по таблице Приложения 3 для заданного уровня значимости α и числа степеней свободы 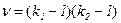 , где k1 и k2 – число групп по одному и второму признакам группировки (число строк и число столбцов в таблице).
, где k1 и k2 – число групп по одному и второму признакам группировки (число строк и число столбцов в таблице).
В рассматриваемом примере ν=(2-1)(2-1)=1, а приняв уровень значимости α=0,01, по таблице Приложения 3 находим χ2табл=6,63. Поскольку рассчитанное значение χ2> χ2табл, значит существует стохастическая зависимость между рассматриваемыми показателями. При независимости признаков частоты теоретического и эмпирического распределений совпадают, а значит χ2=0. Чем больше различия между теоретическими и эмпирическими частотами, тем больше значение χ2 и вероятность того, что оно превысит критическое табличное значение, допустимое для случайных расхождений. Аналогично рассчитываются теоретические частоты и χ2 в таблицах большей размерности.
В корреляционном анализе недостаточно лишь выявить тем или иным методом наличие связи между исследуемыми показателями. Теснота такой связи может быть различной, поэтому весьма важно ее измерить, т.е. определить меру связи в каждом конкретном случае. В статистике для этой цели разработан ряд показателей (коэффициентов), используемых как для количественных, так и для качественных признаков.
Для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности могут быть использованы такие показатели, как коэффициент ассоциации и контингенции (для «четырехклеточных таблиц»), а также коэффициенты взаимной сопряженности Пирсона и Чупрова (для таблиц любой размерности).
Применительно к таблице «четырех полей», частоты которых можно обозначить через a, b, c, d, коэффициент ассоциации (Д. Юла) выражается формулой:
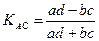 .
.
Его существенный недостаток: если в одной из четырех клеток отсутствует частота (т.е. равна 0), то  1, и тем самым преувеличена мера действительной связи.
1, и тем самым преувеличена мера действительной связи.
Чтобы этого избежать, предлагается (К. Пирсоном) другой показатель – коэффициент контингенции:
 .
.
Рассчитаем коэффициенты и для нашего примера (таблица 8):
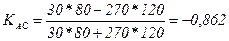 ;
; 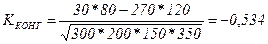
Связь считается достаточно значительной и подтвержденной, если 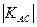 >0,5 или
>0,5 или 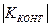 >0,3.
>0,3.
Поэтому в нашем примере оба коэффициента характеризуют достаточно большую обратную зависимость между исследуемыми признаками.
Теснота связи между 2 и более признаками измеряется с помощью коэффициентов взаимной сопряженности Пирсона (11) или Чупрова Ошибка! Источник ссылки не найден., рассчитываемых на основе показателя χ2 :
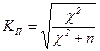 , (11)
, (11) 
В нашем примере 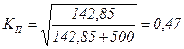 . Рассчитывать коэффициент Чупрова для таблицы «четырех полей» не рекомендуется, так как при числе степеней свободы ν=(2-1)(2-1)=1 он будет больше коэффициента Пирсона (в нашем примере КЧ=0,54). Для таблиц же большей размерности всегда КЧ<КП.
. Рассчитывать коэффициент Чупрова для таблицы «четырех полей» не рекомендуется, так как при числе степеней свободы ν=(2-1)(2-1)=1 он будет больше коэффициента Пирсона (в нашем примере КЧ=0,54). Для таблиц же большей размерности всегда КЧ<КП.
Дата добавления: 2015-10-13; просмотров: 780;
